SVG Paths
SVGs use the same pen metaphor we saw with the <canvas> and one of the most basic approaches to drawing in an SVG is the <path> element. Each <path> should contain a d attribute, which holds the commands used to draw the path. These are very similar to the commands we used with the <canvas> and the CanvasRenderingContext2D we used earlier, but instead of being written as a function call, they are written as a capital letter (indicating what command to carry out) followed by numbers specifying the action. Let’s take another look at our earlier example:
The path’s data is M 100 50 L 100 150 L 300 150 Z. Let’s break it down one command at a time:
M 100 50indicates we should move our pen to point (100, 50).L 100 150indicates we should draw a line from our current position to point (100, 150).L 300 150indicates we should draw a line from our current position to point (300, 150).Zindicates we should close our path, drawing a line to where we started (the point specified in our first command).
Now that we’ve worked through a path example, let’s discuss the specific commands available to us:
Move To
The M x y command indicates we should move to the point (x, y), picking up our pen. It corresponds to ctx.moveTo(x, y).
Line To
The L x y command indicates we should draw a line from our current position to the point (x, y). It corresponds to ctx.lineTo(x, y).
Horizontal Line To
The H x command is shorthand for drawing a horizontal line (the y stays the same) from the current x to the provided x.
Vertical Line To
The V y command is shorthand for drawing a vertical line (the x stays the same) from the current y to the provided y.
Curve To
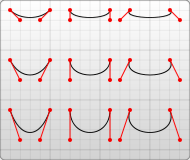
The C cx1 cy1, cx2 cy2, dx, dy is the shorthand for drawing a Bézier Curve from the current position to (dx, dy) using control points (cx1, cy1) and (cx2, cy2). It corresponds to ctx.curveTo(c1x, c1y, c2x, c2y, dx, dy). The MDN web docs has an excellent discussion with visual examples of Bézier curves. A visual example of the role of the effect control points have on a Bézier curve from that article appears below:
Arc To
The A rx ry x-axis-rotation large-arc-flag sweep-flag x y a rx ry x-axis-rotation large-arc-flag sweep-flag dx dy draws an arc. It is roughly analogous to the ctx.drawArc() method, but uses a different way of specifying the arc’s start, end, and direction. You can read a more detailed discussion on the MDN Web Docs
Info
The examples on this page have been adapted from the MDN web docs. You are encouraged to visit these documents for a much more detailed discussion of the concepts and techniques presented here.