Queues in Code

How do we implement queues in code? Like we did with stacks, we will use an array, which is an easily understandable way to implement queues. We will store data directly in the array and use special start and end variables to keep track of the start of the queue and the end of the queue.

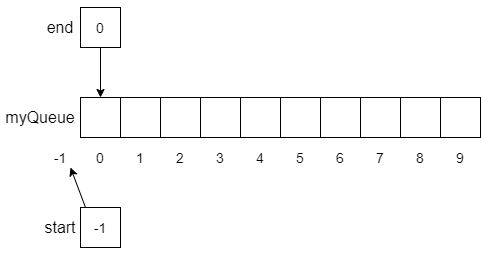
The following figure shows how we might implement a queue with an array. First, we define our array myQueue to be an array that can hold 10 numbers, with an index of 0 to 9. Then we create a start variable to keep track of the index at the start of the queue and an end variable to keep track of the end of the array.

Notice that since we have not put any items into the queue, we initialize start to be -1. Although this is not a legal index into the array, we can use it like we did with stacks to recognize when we have not yet put anything into the queue. As we will see, this also makes manipulating items in the array much simpler. However, to make our use of the array more efficient, -1 will not always indicate that the queue is empty. We will allow the queue to wrap around the array from the start index to the end index. We’ll see an example of this behavior later.

When we want to enqueue an item into the queue, we follow the simple procedure as shown below. Of course, since our array has a fixed size, we need to make sure that we don’t try to put an item in a full array. Thus, the precondition is that the array cannot be full. Enforcing this precondition is the function of the if statement at line 2. If the array is already full, then we’ll throw an exception in line 3 and let the caller handle the situation. Next, we store item at the end location and then compute the new value of end in line 5. Line 6 uses the modulo operator % to return the remainder of the division of $(\text{end} + 1) / \text{length of myQueue}$. In our example, this is helpful when we get to the end of our ten-element array. If end == 9 before enqueue was called, the function would store item in myQueue[9] and then line 4 would cause end to be $(9 +1) % 10$ or $10 % 10$ which is simply $0$, essentially wrapping the queue around the end of the array and continuing it at the beginning of the array.

 1function ENQUEUE (item)
 2  if ISFULL() then
 3    raise exception
 4  end if	
 5  MYQUEUE[END] = ITEM	
 6  END = (END + 1) % length of MYQUEUE
 7  if START == -1
 8    START = 0
 9  end if
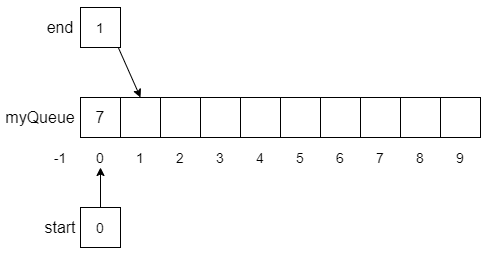
10end function

Given our initial configuration above, if we performed an enqueue(7) function call, the result would look like the following.

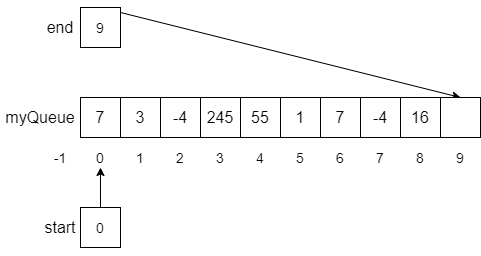
Notice that the value 7 was stored at myQueue[0] in line 5, end was updated to 1 in line 6, and start was set to 0 in line 8. Now, let’s assume we continue to perform enqueue operations until myQueue is almost filled as shown below.

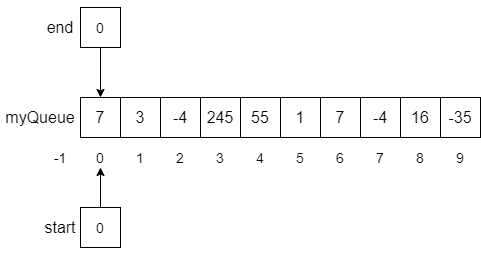
If at this point, we enqueue another number, say -35, the modulo operator in line 6 would help us wrap the end of the list around the array and back to the beginning as expected. The result of this function call is shown below.

Now we have a problem! The array is full of numbers and if we try to enqueue another number, the enqueue function will raise an exception in line 3. However, this example also gives us insight into what the isFull condition should be. Notice that both start, and end are pointing at the same array index. You may want to think about this a little, but you should be able to convince yourself that whenever start == end we will be in a situation like the one above where the array is full, and we cannot safely enqueue another number.

To rectify our situation, we need to have a function to take things out of the queue. We call this function dequeue, which returns the item at the beginning of the queue (pointed at by start) and updates the value of start to point to the next location in the queue. The pseudocode for the dequeue is shown below.

 1function DEQUEUE ()
 2  if ISEMPTY() then
 3    raise exception
 4  end if 
 5  ITEM = MYQUEUE[START]
 6  START = (START + 1) % length of MYQUEUE
 7  if START == END
 8    START = -1
 9    END = 0
10  end if
11  return ITEM
12end function

Line 2 checks if the queue is empty and raises an exception in line 3 if it is. Otherwise, we copy the item at the start location into item at line 5 and then increment the value of start by 1, using the modulo operator to wrap to the beginning of the array if needed in line 6. However, if we dequeue the last item in the queue, we will actually run into the same situation that we ran into in the enqueue when we filled the array, start == end. Since we need to differentiate between being full or empty (it’s kind of important!), we reset the start and end values back to their initial state when we dequeue the last item in the queue. That is, we set start = -1 and end = 0. This way, we will always be able to tell the difference between the queue being empty or full. Finally, we return the item to the calling function in line 11.