The Problem With Arrays

To this point, we have been using arrays as our underlying data structures for implementing linear data structures such as stacks and queues. Given that with stacks and queues we only put items into the array and remove from either the start or end of the data structure, we have been able to make arrays work. However, there are some drawbacks to using arrays for stacks and queues as well as for more general data structures.

  1. We can run out of room in our array for our stacks or queues.
  2. There is no good way to use memory efficiently. We have to use expensive “double” and “halve” capacity operations for stacks and queues when we need to use more or less memory.
  3. Inserting an item into the middle of a sorted list will be very costly in memory. In an array, we will have to move several items to keep the list in order.

While drawbacks 1 and 2 above can be overcome (albeit rather awkwardly) when using arrays for stacks and queues, drawback 3 becomes a real problem when trying to use more general list structures. If we insert an item into the middle of an array, we must move several other items “down” the array to make room.

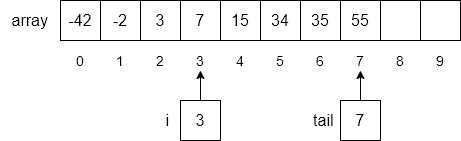
If for example, if we want to insert the number 5 into the sorted array shown below, we have to carry out several steps:

Array Insertion 0 Array Insertion 0

  1. Find the index of the first item whose value is greater than the number we want to insert into the array. We will call this index i,
  2. Shift each item from index i to the end of the list down one place location in the array,
  3. Insert the new item into the array at index i, and
  4. Update the index to the tail of the list.

In our example, step 1 will loop through each item of the array until we find the first number in the array greater than 5. As shown below, the number 7 is found in index 3.

Array Insertion 1 Array Insertion 1

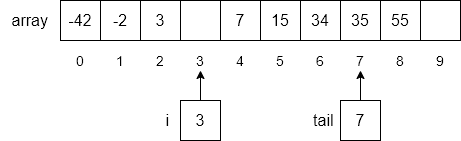
Next, we will use another loop to move each item from index i to the end of the array down by one index number as shown below.

Array Insertion 2 Array Insertion 2

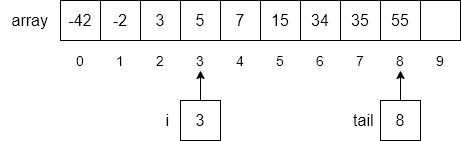
Finally, we will insert our new number, 5, into the array at index 3 and increment tail to 8.

Array Insertion 3 Array Insertion 3

In this operation, if we have $N$ items, we either compare or move all of them, which would require $N$ operations. Of course, this operation runs in order $N$ time.

The same problem occurs when we remove an item from the array. In this case we must perform the following steps:

  1. Search the array to find the first occurrence of the desired number to remove,
  2. Continue searching until we find the last occurrence of the desired number to remove,
  3. Shift each item after the last occurrence of our desired number “up” the array, once for each desired number being removed from the array, and
  4. Update the index to the tail of the list.

A More Flexible Approach

Instead of using arrays to try to hold our lists, a more flexible approach is to build our own list data structure that relies on a set of objects that are all linked together through references to each other. In the figure below we have created a list of numbers that are linked to each other. Each object contains both the number as well as a reference to the next number in the list. Using this structure, we can search through each item in the list by starting sequentially from the beginning and performing a linear search much like we did with arrays. However, instead of explicitly keeping track of the end of the list, we use the convention that the reference in the last item of the list is set to 0, which we call null. If a reference is set to null we interpret this to mean that there is no next item in the list. This “linked list” structure also makes inserting items into the middle of the list easier. All we need to do is find the location in the list where we want to insert the item and then adjust the references to include the new item into the list.

Singly Linked List Overview Singly Linked List Overview

The following figure shows a slightly more complex version of a linked list, called a “doubly linked list”. Instead of just having each item in the list reference the next item, it references the previous item in the list as well. The main advantage of doubly linked lists is that we can easily traverse the list in either the forward or backward direction. Doubly linked lists are useful in applications to implement undo and redo functions, and in web browser histories where we want the ability to go forward and backward in the history.

Doubly Linked List Overview Doubly Linked List Overview

We will investigate each of these approaches in more detail below and will reimplement both our stack and queue operations using linked lists instead of arrays.