Consider the following block of pseudocode:

1. function APPENDER(NUMBER, BASE)
2.     RESULT = ""
3.     loop I from 1 to NUMBER
4.         RESULT = RESULT + BASE
5.         if I MOD 2 = 0
6.             RESULT = RESULT + " "
7.         else
8.             RESULT = RESULT + ", " 
9.     end loop
10.    return RESULT
11. end function

Lets step through the function call with APPENDER(4,'abc') and analyze the memory that the code takes.

Info

Recall that strings are reference variables. As such, string variables hold pointers to values and the value is stored in memory. For the following example, the HEAP refers to what is currently stored in memory and VARIABLE shows the current value of the variable RESULT.

  • Initialization: In line two, we initialize RESULT as an empty string. In the heap, we have the empty string at memory location 0x1. Thus, RESULT is holding the pointer 0x1.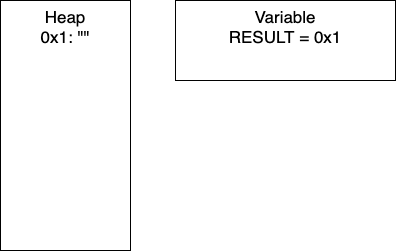 Initialize Initialize

  • I = 1: Now we have entered the loop and on line 4, we add more characters to our string. At this point, we would have entry 0x2 in our heap and our variable RESULT would have the pointer 0x2. Continuing through the code, line 5 determines if I is divisible by 2. In this iteration I = 1, so we take the else branch. We again add characters to our string, resulting in a new entry in 0x3 and our variable RESULT containing the pointer 0x3. In total, we have written 8 characters. We then increment I and move to the next iteration.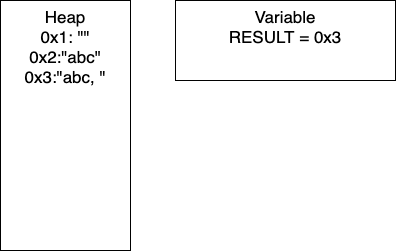 After 1st loop After 1st loop

  • I = 2: We continue the loop and on line 4, we add more characters to our string. At this point, we would have entry 0x4 in our heap and our variable RESULT would have the pointer 0x4. Continuing through the code, line 5 determines if I is divisible by 2. In this iteration I = 2, so we take the if branch. We again add characters to our string, resulting in a new entry in 0x5 and our variable RESULT containing the pointer 0x5. In this iteration, we have written 17 characters. We then increment I and move to the next iteration of the loop.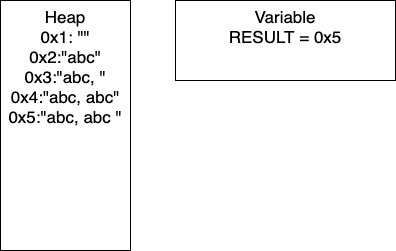 After 2nd loop After 2nd loop

  • I = 3: We continue the loop and on line 4, we add more characters to our string. At this point, we would have entry 0x6 in our heap and our variable RESULT would have the pointer 0x6. Continuing through the code, line 5 determines if I is divisible by 2. In this iteration I = 3, so we take the if branch. We again add characters to our string, resulting in a new entry in 0x7 and our variable RESULT containing the pointer 0x7. In this iteration, we have written 26 characters. We then increment I and thus I = 4 breaking out of the loop. After 3rd loop After 3rd loop

We can do some further analysis of the memory that is required for this particular block.

Iteration Memory Entries Total Character Copies
1 3 8
2 5 8 + 17 = 25
3 7 25 + 26 = 51
4 9 51 + 35 = 86
. . .
n 2n + 1 (9n2 + 7n)/2

You need not worry about creating the equations! Based on this generalization, if the user wanted to do 100K iterations, say for gene sequencing, there would be (2x100,000 - 1) = 200,001 memory entries and (9x100,0002 + 7x100,000)/2 = 45 billion character copies. This behavior is not exclusive to strings; this will occur for any immutable type.

While this example is contrived, it is not too far off the mark. Another caveat to this analysis is that, depending on our programming language, there will be a periodic ‘memory collection’; there wont be 200K memory addresses occupied at one time. Writing to memory in this way can be costly in terms of time, which in industry is money.