An important application for these traversals is the ability to find a path between two nodes. This has many applications in railroad networks as well as electrical wiring. With some modifications to the traversals, we can determine if electricity can flow from a source to a target. We will modify depth first and breadth first traversals in similar ways.
There are three cases that can happen when we search for a path between nodes:
- No Path: will return nothing
- One Path: will return the path
- Multiple Paths: will return A path
With these searches, we are not guaranteed to return the same path if there are multiple paths.
We will call these Depth First Search (DFS) and Breadth First Search (BFS). In both traversals, we have added the following extra lines: 4, 9-16, and 22 through the end.
First, we have the addition of PARENT_MAP which will be a dictionary to keep track of how we get from one node to another. We will use the convention of having the key be the child and the value be the parent. While we use the terms child and parent, this is not exclusive to trees.
The ending portion starting at line 22, will add entries to our dictionary. If we haven’t already found an edge to NODE, then we will add the edge that we are currently on.
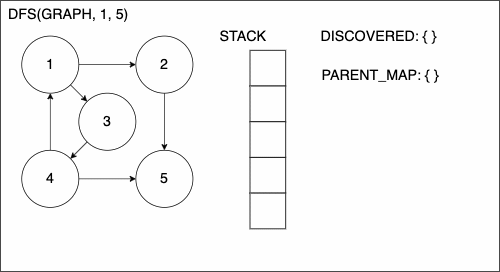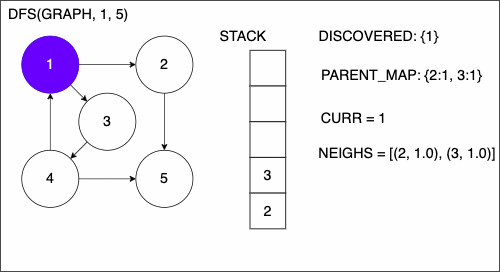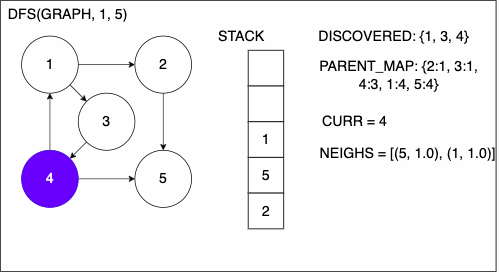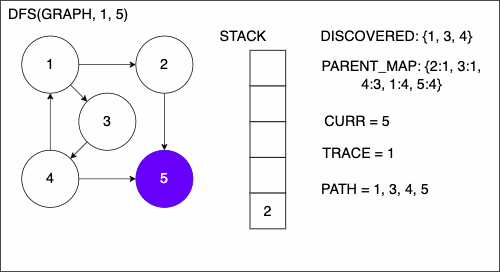
The other addition is the block of code from line 9 to 16. We will enter this if block if the node that we are currently at is the target. This means that we have finally found a path from the source node to the target node. The process in this segment of code will backtrack through the path and build the path.
Depth-First Search
1function DEPTHFIRSTSEARCH(GRAPH,SRC,TAR)
2 STACK = empty array
3 DISCOVERED = empty set
4 PARENT_MAP = empty dictionary
5 append SRC to STACK
6 while STACK is not empty
7 CURR = top of the stack
8 if CURR not in DISCOVERED
9 if CURR is TAR
10 PATH = empty array
11 TRACE = TAR
12 while TRACE is not SRC
13 append TRACE to PATH
14 set TRACE equal to PARENT_MAP[TRACE]
15 reverse the order of PATH
16 return PATH
17 add CURR to DISCOVERED
18 NEIGHS = neighbors of CURR
19 for EDGE in NEIGHS
20 NODE = first entry in EDGE
21 append NODE to STACK
22 if PARENT_MAP does not have key NODE
23 in the PARENT_MAP dictionary set key NODE with value CURR
24 return nothingDepth-First Search Example
Breadth-First Search
1function BREADTHFIRSTSEARCH(GRAPH,SRC,TAR)
2 QUEUE = empty queue
3 DISCOVERED = empty set
4 PARENT_MAP = empty dictionary
5 add SRC to DISCOVERED
6 add SRC to QUEUE
7 while QUEUE is not empty
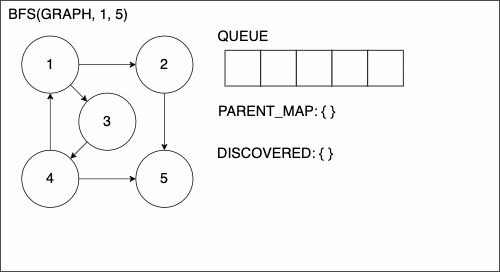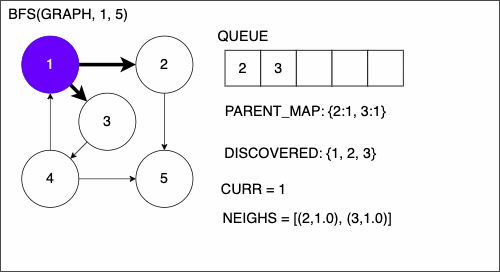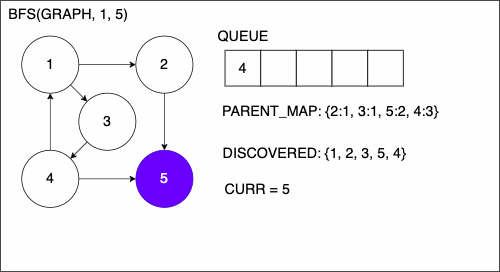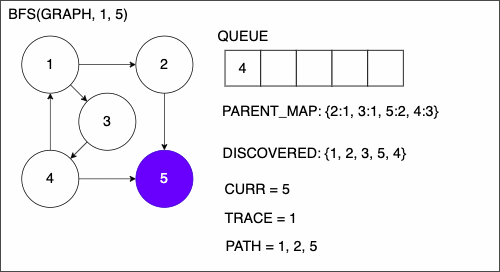
8 CURR = first element in QUEUE
9 if CURR is TAR
10 PATH = empty list
11 TRACE = TAR
12 while TRACE is not SRC
13 append TRACE to PATH
14 set TRACE equal to PARENT_MAP[TRACE]
15 reverse the order of PATH
16 return PATH
17 NEIGHS = neighbors of CURR
18 for EDGE in NEIGHS
19 NODE = first entry in EDGE
20 if NODE is not in DISCOVERED
21 add NODE to DISCOVERED
22 if PARENT_MAP does not have key NODE
23 in the PARENT_MAP dictionary set key NODE with value CURR
24 append NODE to QUEUE
25 return nothing