Summary 1
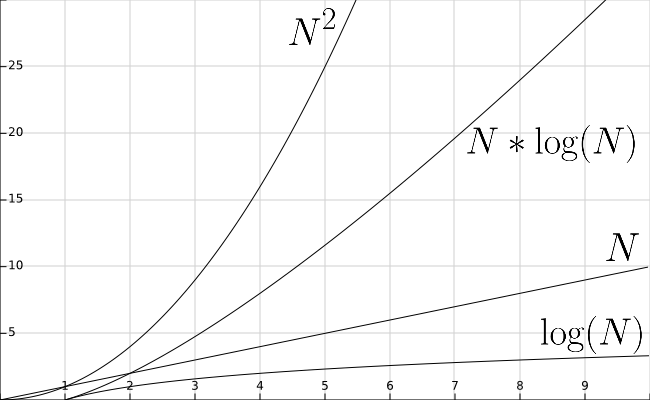
This page will be devoted to summarizing our performance discussions. Below, we have included a graph for a frame of reference for the various functions.
Generic Trees
In the following, $n$ denotes the number of nodes in the tree.
- Insert: 1 if we have the parent but $n$ if we have to find the parent
- Access: 1 if we want to access the root but $n$ otherwise
- Find: $n$
- Delete: $n$ if we have to find the parent
- Memory: $n$
Tries
In the following, $m$ denotes the length of a word and $n$ denotes the number of words in the trie.
- Insert: $m$
- Access: $m$
- Find: $m$
- Delete: $m$
- Memory: $n\times m$
Binary Trees
In the following, $n$ denotes the number of nodes in the tree.
- Insert: $log_2(n)$ when balanced but $n$ otherwise
- Access: $log_2(n)$ when balanced but $n$ otherwise
- Find: $log_2(n)$ when balanced but $n$ otherwise
- Delete: $log_2(n)$ when balanced but $n$ otherwise
- Memory: $n$
Matrix Graph
In the following, $n$ denotes the number of nodes in the graph.
- Insert Node: $n$
- Access Node: 1
- Find Node: $n$
- Delete Node: $n$
- Insert Edge: 1
- Access Edge: 1
- Find Neighbors: $n$
- Delete Edge: 1
- Memory: $n^2$
List Graph
In the following, $n$ denotes the number of nodes in the graph and $e$ denotes the number of edges.
- Insert Node: $n$
- Access Node: 1
- Find Node: $n$
- Delete Node: $n$
- Insert Edge: $n$
- Access Edge: $n$
- Find Neighbors: 1
- Delete Edge: $n$
- Memory: $n+e$
Priority Queue
In the following, $n$ denotes the number of elements in the priority queue.
- Insert: $log_2(n)$
- Access Minimum: 1
- Find: $n$
- Remove Minimum: $log_2(n)$
- Heapify: $n$
- Memory: $n$