Programming by Contract

YouTube Video

In this course, we will learn how to develop several different data structures, and then use those data structures in programs that implement several different types of algorithms. However, one of the most difficult parts of programming is clearly explaining what a program should do and how it should perform.

So far, we’ve used UML class diagrams to discuss the structure of a program. It can give us information about the classes, attributes, and methods that our program will contain, as well as the overall relationships between the classes. We can even learn if attributes and methods are private or public, and more.

However, to describe what each method does, we have simply relied on descriptions in plain language up to this point, with no specific format at all. In this module, we’ll introduce the concept of programming by contract to help us provide more specific information about what each method should do and the expectations we can count on based on the inputs and outputs of the method.

Specifically, we’ll learn about the preconditions that are applied to the parameters of a method to make sure they are valid, the postconditions that the method will guarantee if the preconditions are met, and the invariants that a loop or data structure will maintain.

Finally, we can put all of that information together to discuss how to prove that an algorithm correctly performs the task it was meant to, and how to make sure that it works correctly in all possible cases.

Preconditions

First, let’s discuss preconditions. A precondition is an expectation applied to any parameters and existing variables when a method or function is called. Phrased a different way, the preconditions should all be true before the method is called. If all of the preconditions are met, the function can proceed and is expected to function properly. However, if any one of the preconditions are not met, the function may either reach an exception, prompt the user to correct the issue, or produce invalid output, depending on how it is written.

Example - Area of a Triangle

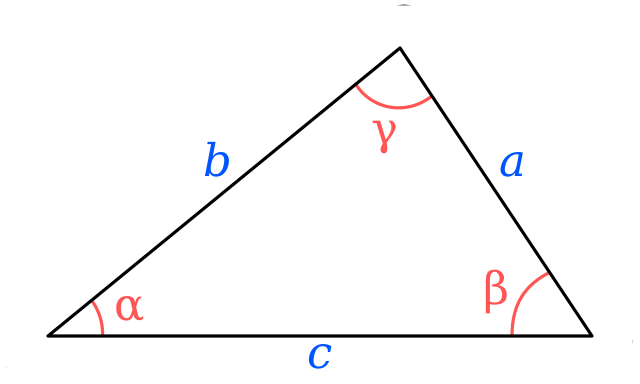
Let’s consider an example method to see how we can define the preconditions applied to that method. In this example, we’re going to write a method triangleArea(side1, side2, side3) that will calculate the area of a triangle, given the lengths of the sides of the triangle.

So, to determine what the preconditions of that method should be, we must think about what we know about a triangle and what sort of data we expect to receive.

For example, we know that the length of each side should be a number. In addition, those lengths should all be positive, so each one must be strictly greater than $0$.

We can also determine if we expect the length to be whole numbers or floating-point numbers. To make this example simpler, let’s just work with whole numbers.

When looking at preconditions, determining the types and expected range of values of each parameter is a major first step. However, sometimes we must also look at the relationship between the parameters to find additional preconditions that we must consider.

^[File:TriangleInequality.svg. (2015, July 10). Wikimedia Commons, the free media repository. Retrieved 23:22, January 21, 2020 from https://commons.wikimedia.org/w/index.php?title=File:TriangleInequality.svg&oldid=165448754.]

For example, the triangle inequality states that the longest side of a triangle must be strictly shorter than the sum of the other two sides. Otherwise, those sides will not create a triangle. So, another precondition must state that the sides satisfy the triangle inequality.

All together, we’ve found the following preconditions for our method triangleArea(side1, side2, side3):

1. side1, side2 and side3 each must each be an integer that is strictly greater than $0$
2. side1, side2 and side3 must satisfy the triangle inequality

Precondition Failures

What if our method is called and provided a set of parameters that do not meet the preconditions described above? As a programmer, there are several actions we can take in our code to deal with the situation.

Exceptions

One of the most common ways to handle precondition failures is to simply throw or raise exceptions from our method as soon as it determines that the preconditions are not met. In this way, we can quickly indicate that the program is unable to perform the requested operation, and leave it up to the code that called that method to either handle the exception or ignore it and allow the program to crash.

This method is best used within the model portions of a program written using the Model-View-Controller or MVC architecture. By doing so, this allows our controller to react to problems quickly, usually by requesting additional input from the user using the view portion of the program.

Prompt User

In simpler programs, it is common for the code to simply handle the precondition failure by asking the user for new input. This is commonly done in programs that are small enough to fit in a single class, instead of being developed using MVC architecture.

Incorrect Output

Of course, we could choose to simply ignore these precondition failures and allow our code to continue running. IN that case, if the preconditions are not met, then the answer we receive may be completely invalid. On the next page, we’ll discuss how failed preconditions affect whether we can trust our method’s output.

Postconditions

Next, we can discuss postconditions. A postcondition is a statement that is guaranteed to be true after a method is executed, provided all of the preconditions were met. If any one of the preconditions were not met, then we can’t count on the postcondition being true either. This is the most important concept surrounding preconditions and postconditions.

Example - Area of a Triangle

On the last page, we discussed the preconditions for a method triangleArea(side1, side2, side3) that will calculate the area of a triangle given the lengths of its sides. Those preconditions are:

1. side1, side2 and side3 each must each be an integer that is strictly greater than $0$
2. side1, side2 and side3 must satisfy the triangle inequality

So, once the method completes, what should our postcondition be? In this case, we want to find a statement that would be always true if all of the preconditions are met.

Since the method will be calculating the area of the triangle, the strongest postcondition we can use is the most obvious one:

1. The method will return the area of a triangle with side lengths side1, side2 and side3

That’s really it!

Of course, there are a few other postconditions that we could consider, especially when we start working with data structures and objects. For example, one of the most powerful postconditions is the statement:

1. The values of the parameters are not modified from their original values

When we call a method that accepts an array or object as a parameter, we know that we can modify the values stored in that array or object because the parameter is handled in a call-by-reference fashion in most languages. So, if we don’t state that this postcondition applies, we can’t guarantee that the method did not change the values in the array or object we provided as a parameter.

Precondition Failures: Incorrect Output

So, what if the preconditions are not met? Then what happens?

As we discussed on the previous page, if the preconditions are not met, then we cannot guarantee that the postcondition will be true once the method executes. In fact, it may be decidedly incorrect, depending on how we implement the method.

^[File:Triangle with notations 2 without points.svg. (2018, December 5). Wikimedia Commons, the free media repository. Retrieved 00:03, January 22, 2020 from https://commons.wikimedia.org/w/index.php?title=File:Triangle_with_notations_2_without_points.svg&oldid=330397605.]

For example, the simplest way to find the area of a triangle given the lengths of all three sides is Heron’s formula , which can be written mathematically as:

$$ A = 1/4 \sqrt{(a + b + c)(-a + b + c)(a - b + c)(a + b - c)} $$

Since this is a mathematical formula, it is always possible to get a result from it, even if all of the preconditions are not met. For example, the inputs could be floating-point values instead of integers, or they may not satisfy the triangle inequality. In that case, the function may still produce a result, but it will not represent the actual area of the triangle described, mainly because the parameters provided describe a triangle that cannot exist in the real world. So, we must always be careful not to assume that a method will always provide the correct output unless we provide parameters that make all of its preconditions true.

Invariants

YouTube Video

Another concept related to preconditions and postconditions is the loop invariant. A loop invariant is a statement should be true after each iteration of a loop, provided the loop’s preconditions are all true before the start of the loop. Yes, that’s right—we can think of a loop as a miniature method within a method, with its own set of preconditions and postconditions.

Example - Maximum

For this example, let’s consider a method maximum(numbers) that gets an array of numbers as input, and returns the maximum value stored in that list. So, we can start by listing the preconditions of the method:

1. numbers is an array containing at least one numerical value, either a floating point or an integer

Thankfully, that one precondition covers all of our bases. Likewise, we can define our postcondition pretty easily as well:

1. The method returns the maximum value stored in the numbers array
2. The numbers array is not modified by the method

There we go! Hopefully it is easy to see how the preconditions and postconditions help us build a better definition of what operations should be performed by the method.

Method Pseudocode

Now that we’ve built our method’s preconditions and postconditions, let’s quickly write the method in pseudocode so we can see what it would look like.

function MAXIMUM(NUMBERS)
    MAX = NUMBERS[0]
    loop I from 1 to length of NUMBERS
        if NUMBERS[I] > MAX
            MAX = NUMBERS[I]
        end if
    end loop
    return MAX
end function

We’ve seen methods like this several times already, since calculating the maximum value from an array of values is a very common task. This time, however, let’s discuss the preconditions, postconditions and invariants of the loop inside of this method.

Preconditions

First, we can establish an important precondition at the beginning of the loop. In this case, the precondition that best describes the value stored in MAX is:

1. MAX contains the maximum value stored in NUMBERS up to and including index $0$.

In this way, we’ve directly tied our precondition to the values that exist in the method already, and we’ve accurately described the value that MAX is currently storing.

Loop Invariant

Next, we can determine what the loop invariant should be. This is a statement that should be true after each iteration of the loop, provided the precondition is true. Usually we want to try and relate it to the precondition somehow, and how it changes after each iteration of the loop. So, let’s consider the following loop invariant:

1. MAX contains the maximum value stored in NUMBERS up to and including index $I$.

Hmm, that’s almost exactly the same as the precondition, isn’t it? That’s what we’re going for here. In this way, we can easily describe what the loop does after each iteration based on how it updates the value in MAX, keeping the loop invariant true. We call that “maintaining the loop invariant.”

Postcondition

Finally, we can define the postcondition of the loop. This is pretty simple, since it is the same as the loop invariant, but this time we can say that I is equal to the end of the loop. So, our postcondition is simply:

1. MAX contains the maximum value stored in NUMBERS up to and including the last index.

That’s all there is to it! By defining a precondition, invariant, and postcondition for our loop, we can very accurately describe exactly what that loop should do. On the next page, we’ll see how we can put all of those together to show that our method works correctly.

Correctness

YouTube Video

If we have defined the correct preconditions, postconditions, and invariants for our code, we can then use those to prove that our code correctly performs its intended operation.

In this course, we won’t ask you to do any of this yourself, but it is important to understand what is going on in the background and how this process works. We can use the concepts of preconditions and postconditions when grading your code using our Autograder—in fact, that’s really how it works!

Proving Correctness

To prove correctness of a method, we can generally follow this process:

1. Establish (or assume) that the method’s preconditions are all true
2. Use the preconditions and the code to demonstrate that any invariants within the code are always true
   1. If the code contains a loop, we can repeat this process for preconditions and postconditions of the loop
3. Use the preconditions and invariants to show that the postcondition is true

Let’s do this for our maximum() method described on the previous page. Here is the pseudocode once again:

function MAXIMUM(NUMBERS)
    MAX = NUMBERS[0]
    loop I from 1 to length of NUMBERS
        if NUMBERS[I] > MAX
            MAX = NUMBERS[I]
        end if
    end loop
    return MAX
end function

Here are the associated conditions we established as well:

Method Precondition: NUMBERS is an array containing at least one numerical value, either a floating point or an integer Loop Precondition: MAX contains the maximum value stored in NUMBERS up to and including index $0$. Loop Invariant: MAX contains the maximum value stored in NUMBERS up to and including index $I$. Loop Postcondition: MAX contains the maximum value stored in NUMBERS up to and including the last index. Method Postconditions: The method returns the maximum value stored in the NUMBERS array, and the NUMBERS array is not modified by the method

Now that we have that information, we can discuss the correctness of the method.

A Simple Proof

To begin, we assume that the method’s preconditions are true. Therefore, we know that NUMBERS is an array containing at least one numerical value. Earlier in this chapter, we learned that we can’t assume that the method works if the preconditions are false, so we can always begin our proof by assuming they are true.

Next, we have to use the code as well as the method’s preconditions to establish that the loop’s preconditions are true. In the code, we see that we set the value of MAX equal to the first element in the NUMBERS array. So, since there is only that value in the NUMBERS array up to and including index $0$, it is easy to say that it is indeed the maximum value. So, we’ve shown that our loop’s precondition is true.

After that, we have to show that the loop invariant is true after each iteration of the loop. A proper proof would involve a technique called proof by induction, which is more advanced than we want to cover in this course. However, a simple way to think about it is to say that the value in MAX contains the largest value in the list that we’ve seen so far. On each loop iteration, we look at one more value. If it is larger than MAX, then it becomes the new MAX value. Otherwise, we know that the maximum value we’ve seen so far hasn’t changed. So, we can show that our loop invariant is always true after each loop iteration.

Finally, once we reach the end of the loop, we’ve looked at every element including the last index, and found the MAX value, so it is easy to see that our loop postcondition is true.

Then, we can quickly use that loop postcondition to understand that the MAX value is really the largest in the NUMBERS array, which means that the first part of our method’s postcondition is also true.

But wait! What about the second part, that insists that we did not modify the contents of the numbers array? Thankfully, we can quickly look at our code and determine that we are not assigning a value into the array, nor do we call any functions on the array, so it is easy to show that our code has not modified it in any way.

There we go! This is a quick example for how we can use preconditions, postconditions, and invariants to help understand our code and whether it works correctly.

On the next page, we’ll learn about unit testing and how we can write our own code to verify that our code works correctly.

Unit Testing

Once we’ve written a program, how can we verify that it works correctly? There are many ways to do this, but one of the most common is unit testing.

Unit Testing

Unit testing a program involves writing code that actually runs the program and verifies that it works correctly. In addition, many unit tests will also check that the program produces appropriate errors when given bad input, or even that it won’t crash when given invalid input.

For example, a simple unit test for the maximum() method would be:

function MAXIMUMTEST()
    ARRAY = new array[5]
    ARRAY[0] = 5
    ARRAY[1] = 25
    ARRAY[2] = 10
    ARRAY[3] = 15
    ARRAY[4] = 0
    RESULT = MAXIMUM(ARRAY)
    if RESULT == 25:
        print "Test Passed"
    end if
end function

This code will simply create an array that we know the maximum value of, and then confirm that our own maximum() method will find the correct result.

Of course, this is a very simplistic unit test, and it would take several more unit tests to fully confirm that the maximum() method works completely correctly.

However, it is important to understand how this test relates to the preconditions and postconditions that were established on previous pages. Here, the unit tests creates a variable ARRAY which is an array of at least one numerical value. Therefore, it has met the preconditions for the maximum() method, so we can assume that if maximum() is written correctly, then the postconditions will be true once it is has executed. This is the key assumption behind unit tests.

Performance of Algorithms

The performance of our algorithms is very important, since the difference between good algorithms and bad algorithms on very large data sets can often be measured in terms of days of execution time. Thus, efficiency will be one of the key issues we will look at when designing algorithms.

For example, one simple problem involves finding the largest sum of contiguous elements in an array. So, if we have the array:

[−2, 1, −3, 4, −1, 2, 1, −5, 4]

we could find that the contiguous sequence of:

[4, −1, 2, 1]

sums to $6$, which is the largest sum of any contiguous subsequences of this array.

A simple solution to this problem might involve finding all possible subsequences of the array and adding them, which could take a very long time. In fact, if the array contains $n$ elements, it might take $n^3$ steps to solve it. However, with a little ingenuity, we can actually solve this problem using many fewer steps, even as few as $n$ steps itself.

When we try to solve a problem, it is often helpful to look at multiple solutions to the problem and compare them before choosing our final design. Just the act of trying to find multiple ways to solve the same problem stimulates creativity and promotes mental elasticity and speed of thought. Selecting a solution from several different choices following rigorous and objective criteria enables us to improve fundamental life skills such as simply knowing how to make decisions! In fact, the very attempt at solving a problem in a variety of ways forces us to look our problems from different perspectives, which is the catalyst of all scientific discoveries.

Throughout this section, we will develop two solutions to the problem of finding the maximum max and minimum min of a list of N numbers (defined as list[N]) as an example. We will develop both solutions and then evaluate their performances in terms of both execution time and memory space.

Max and Min - Linear

YouTube Video

Let’s start by considering one number from the list at a time.

Base Case

When we have received just one number, this number is both the maximum and the minimum. In the initial state, you have max holding the maximum, and min holding the minimum. The invariant is the following:

1. The variable max holds the maximum of all the numbers considered so far
2. The variable min holds the minimum of all the numbers considered so far

The algorithm is depicted by the following flowchart and pseudocode:

print "Enter a Number:"
input X
MAX = X
MIN = X

The Next Number

Then, our program will enter a loop to read 10 more numbers from the user. So, we’ll need to perform the following process during each iteration of the loop:

1. compare the value in max with this new number and update the max value if the new number is greater. In this way, the invariant is preserved.
2. compare the value in min with this new number and update the min value if the new number is smaller. In this way, the invariant is preserved.

This part of the program is depicted by the following flowchart and pseudocode:

loop I from 1 to 10
    print "Enter a Number:"
    input X
    if X > MAX
        MAX = X
    end if
    if X < MIN
        MIN = X
    end if
end loop

After you’ve considered the second number, you end up in the same situation at the beginning: you have a maximum and a minimum value of the numbers input by the user so far. You have found an invariant if you verify that the preconditions before executing an iteration of the loops are the same as the conditions at the end of the loop, known as postconditions:

• Loop preconditions:
  1. The variable max holds the maximum value among all the numbers considered so far
  2. The variable min holds the minimum value among all the numbers considered so far
  3. The new input considered is a number
• Loop postconditions:
  1. The variable max holds the maximum value among all the numbers considered so far
  2. The variable min holds the minimum value among all the numbers considered so far
• Loop invariant:
  1. The variable max holds the maximum value among all the numbers considered so far
  2. The variable min holds the minimum value among all the numbers considered so far

You can then generalize the solution for the nth input: when you consider the nth number, compare it with the values in max and min, updating them if necessary. In each step, we can show that the invariant holds.

A full flowchart of this program can be found by clicking the following link:

Min Max Flowchart

It is helpful to have this diagram available in a second browser tab for review on the next few pages.

Max and Min - Pairs

YouTube Video

Another solution consists of comparing the numbers in pairs, instead of one at a time.

Base Case

When we have received just one number, this number is both the maximum and the minimum. In the initial state, you have max holding the maximum, and min holding the minimum. The invariant is the following:

1. The variable max holds the maximum of all the numbers considered so far
2. The variable min holds the minimum of all the numbers considered so far

The algorithm is depicted by the following flowchart and pseudocode:

print "Enter a Number:"
input X
MAX = X
MIN = X

The Next Two Numbers

In this program, instead of just considering one number at a time, we’ll ask the user to input two numbers. Then, we can determine which of those two inputs is larger (we’ll call it lastmax), and compare it to the value in max. Similarly, we can do the same for the smaller value (called lastmin) and min. Would this program be more efficient?

The algorithm is depicted by the following flowchart and pseudocode:

loop I from 1 to 10 step by 2:
    output "Enter a Number:"
    input X
    output "Enter a Number:"
    input Y
    if X > Y
        LASTMAX = X
        LASTMIN = Y
    else
        LASTMAX = Y
        LASTMIN = X
    end if
    if LASTMAX > MAX
        MAX = LASTMAX
    end if
    if LASTMIN < MIN
        MIN = LASTMIN
    end if
end loop

Once again, we can easily show that the same loop preconditions, postconditions, and invariants work for this loop:

• Loop preconditions:
  1. The variable max holds the maximum value among all the numbers considered so far
  2. The variable min holds the minimum value among all the numbers considered so far
  3. The new inputs considered are a number
• Loop postconditions:
  1. The variable max holds the maximum value among all the numbers considered so far
  2. The variable min holds the minimum value among all the numbers considered so far
• Loop invariant:
  1. The variable max holds the maximum value among all the numbers considered so far
  2. The variable min holds the minimum value among all the numbers considered so far

A full flowchart of this program can be found by clicking the following link:

Min Max Flowchart

It is helpful to have this diagram available in a second browser tab for review on the next few pages.

Time Complexity

YouTube Video

It is very useful to compare the two solutions to choose one. In general, you can compare the two solutions by considering:

1. The time required to execute it
2. The amount of memory it requires
3. The number of instructions used, and also the understandability of the code

Time Complexity

To compare programs in terms of the time we can estimate the running time, or time it takes to complete its work. If the program performs operations on a large set of data, you can also check the run time by using the timer available in your programming language. This type of algorithm profiling is called experimental algorithm evaluation.

You can also estimate the time by counting the number of comparisons and assignments performed by the two programs since comparison and assignments are the fundamental operations that allow you to find the smallest and the largest element.

Let’s do this analysis for both the linear and pairs solution to the problem of finding the minimum and maximum values in a list of numbers. For this analysis, we’ll just look at the code inside the loop, and ignore any code before the loop that initializes variables, since both programs have the same code there.

Comparisons

The linear program performs two comparisons, x > max and x < min each time a new number is considered. If the algorithm considers N numbers, the total number of comparisons is $N * 2$ or $2N$ comparisons.

The pairs program makes three comparisons every time it considers two elements: x > y, lastmax > max and lastmin < min If the algorithm considers N numbers, the total number of comparison is $N/2 * 3$ or $3/2 N$ comparisons.

If we assume that our list is holding a large number of values, then we can see a major difference in the time required to complete the program. Put another way, we can observe that the difference in efficiency between the two programs increases as N increases. Assuming N is $1,000$, the linear program makes $2,000$ comparisons, while the pairs program makes $1,500$ comparisons.

Of course, data sizes in real programs can be much larger. For example, Google currently indexes around 50 billion web pages! So, a list that contains $1,000$ numbers looks pretty small by comparison.

Assignments

For the assignments, you can count them. For the linear solution, the following situations could occur:

1. The new number updates the maximum. If the new number is the maximum it will be greater than the minimum, so no update is required for the minimum
2. The new number update the minimum. If the new number is the minimum it will be lower than the maximum so no updated are required for the maximum
3. If the new number is between the minimum and the maximum value no updates are required

So, in the worst-case, the algorithm performs $N$ assignments. For example, consider a situation where the list is already sorted in increasing order. In that case, we’ll have to update the maximum value each time, resulting in $N$ assignments.

In the pairs solution, for every two numbers considered causes the following assignments to be computed:

1. Two assignments for updating the lastmax and lastmin. These two assignments are done in any case.
2. From zero to two assignments to update the min and the max, depending on the results of the comparisons.

Therefore, the number of assignments is $2$ in the best case, $4$ in the worst case, and $3$ in the average case. Hence, with $N$ numbers, the number of assignments is $N/2 * 2$ or $N$ in the best case, $2N$ in the worst case and $3/2N$ in the average case. The number of assignments is greater with the second algorithm. But, could we do better in this last case?

Which is Better?

So, how can we determine which is better? Let’s look at a couple of situations.

For example, if we have a list of 1000 numbers, we can find the following number of steps for each program. First, let’s consider the worst case performance, taking the largest values for each.

1. Linear: $2N$ or $2000$ comparisons + $N$ or $1000$ assignments, so $3000$ total steps
2. Pairs: $3/2 * N$ or $1500$ comparisons + $2N$ or $2000$ assignments, to $3500$ total steps

As we can see, the pairs program requires more steps in total than the linear program. So, it appears that it might be the best choice.

However, not every program will be a worst case. So, let’s look at the best case performance for each one:

1. Linear: $2N$ or $2000$ comparisons + $0$ assignments (ignoring the small number of initial assignments), so $2000$ total steps
2. Pairs: $3/2 * N$ or $1500$ comparisons + $N$ or $1000$ assignments, to $2500$ total steps

Again, we see that the pairs program still requires more steps than the linear program, though both programs run faster in the best case than the worst case.

Finally, we can do the same for the average case performance:

1. Linear: $2N$ or $2000$ comparisons + $N/2$ assignments, so $2500$ total steps
2. Pairs: $3/2 * N$ or $1500$ comparisons + $3/2 * N$ or $1500$ assignments, to $3000$ total steps

There we go! As we can see, in each case the linear program actually performs better than the pairs program, even though we know that the pairs program will only run the loop half as many times as the linear program. The extra comparisons and assignments make the program take more time!

Space Complexity

We can also look at a program based on the amount of space, or memory, that it uses. In this case, we are looking at the number of variables that are needed, and also the size of any lists, arrays, or more advanced data structures used.

The comparison in terms of space leads us to observe that the linear solution uses, in addition to the input value x for each iteration of the loop, also the max and min variables. So, there are just 3 more variables to keep track of.

The pairs solution uses, in addition to the two input values x and y for each iteration of the loop, two variables for the lastmax and lastmin as well as the global max and min variables. So, there are 6 more variables to keep track of in this solution

Therefore, the linear solution is more space-efficient since it requires only three variables.

A Bigger Example

Let’s consider a bigger example program, just to see the impact of space complexity when analyzing a program. Consider a program that will compute the result of multiplying two numbers from $1$ through $10$. So, there are 10 numbers we need to consider as both operands.

One possible solution would be to pre-compute all possible answers in a 10 by 10 array, which would contain 100 elements. A diagram of this is shown below.

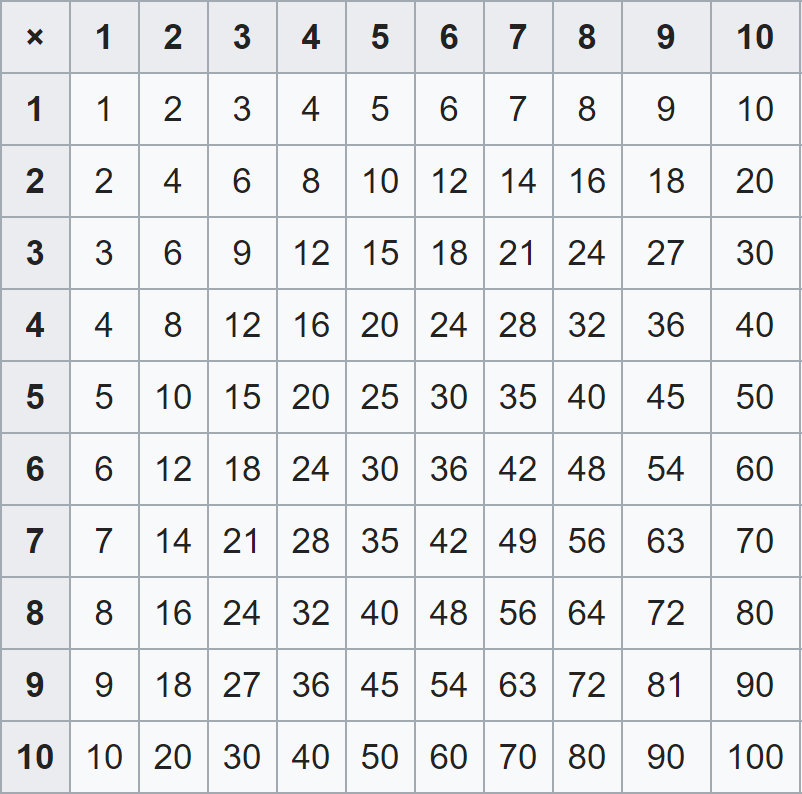
^[Wikipedia contributors. (2020, January 25). Multiplication table. In Wikipedia, The Free Encyclopedia. Retrieved 02:06, January 28, 2020, from https://en.wikipedia.org/w/index.php?title=Multiplication_table&oldid=937470066]

This is a very inefficient program in terms of space complexity, since it requires $N^2$ spaces in memory for $N$ possible operand values.

Of course, we already know that we could write a program that could simply calculate and return the answer based on the input values, so this example is a bit worthless in practice. However, on some small, embedded systems such as a smart watch or nano-machine, we might discover that it is better to use memory than to spend time calculating a result on such a slow processor, so there are times where having higher space complexity helps save time in the long run.

Code Complexity

Lastly, when analyzing a program, we must also consider the complexity of the code used to write the program. Code complexity can refer to many things, but in general we use it to describe how many lines of code are included the program, as well as how easy it is to understand what the program does.

Lines of Code

One of the most common ways to measure the size of a program is the number of lines of code, or LOC, of the program. This can be a very rough estimate of the size of the program, since, in general, a longer program with more lines of code may be more complex than a shorter program with fewer lines.

So, if we can find a solution to a problem that requires many fewer lines of code than another solution, that is one factor to consider. Of course, the solution with fewer lines of code may be more complex in terms of time or space!

Understandability

The other important measure of code complexity deals with how easy it is to understand what the program does. Sometimes we can write a program that only takes a few lines of code, but it is so complex that it is difficult to really understand how it works.

For example, consider this line of pseudocode - can you determine what it does?

return (X > 0) and ((X % 10) + (INT((X % 100) / 10))) < 5

It is pretty difficult to understand. Can we rewrite this program to make it easier to understand? Consider the following code:

if X <= 0
    return FALSE
else
    ONES_PLACE = X % 10
    TENS_PLACE = X % 100
    SUM_LAST_TWO_DIGITS = TENS_PLACE + ONES_PLACE
    if SUM_LAST_TWO_DIGITS < 5
        return TRUE
    else
        return FALSE
    end if
end if

This program is pretty easy to follow. First, it will determine if X is 0 or a negative number, and return FALSE if so. Then, it will find the last two digits of the number, corresponding to the ones and the tens place, and sum them. Finally, if the sum of the last two digits is less than $5$, it will return TRUE. Otherwise, it will return FALSE.

As it turns out, these two programs do the exact same thing! However, from the single line of code in the first program, it is very difficult to decipher exactly what it does. The second program, even though it is much longer, is much easier to understand. In addition, when run on a real computer, both of these programs will take nearly the same amount of time to run.

Complexity Triad

As we’ve seen, we can describe the complexity of a program in terms of three values: the time it takes to run, the space it requires in memory, and the size and understandability of the code. However, how do we know which of those measures is the most important?

Unfortunately, that is a difficult question to answer. In general, we want to reduce each of these levels of complexity, but sometimes there are trade-offs. For example, a program that runs quickly may require lots of extra memory, or it could even require really complex code.

The world of business uses a simple triad to understand these trade-offs, as shown in the diagram below:

^[File:Project-triangle.svg. (2020, January 12). Wikimedia Commons, the free media repository. Retrieved 02:41, January 28, 2020 from https://commons.wikimedia.org/w/index.php?title=File:Project-triangle.svg&oldid=386979544.]

Along with this diagram comes the saying: “Fast. Good. Cheap. Pick any two.” It helps express the difficulty in finding a perfect program that does not contain at least one level of complexity.

Thankfully, most modern computers have a sufficiently fast processor and ample memory that most programs can run easily, even without worrying about reducing the space and time complexity of the program. So, it may seem that the most important measure to focus on is code complexity: we should strive to write readable and understandable code.

However, as we build larger programs and deal with more input data, time and space complexity quickly become more important. So, it is important to consider each measure independently, and do the best we can to build programs that run quickly, use a minimal amount of memory, and aren’t so complex that they are difficult to understand.

Programming by Contract and Performance Summary

In this module, we covered two major topics that will help us understand the data structures and algorithms we’ll learn in this course. First, we learned about the use of preconditions, postconditions, and loop invariants to help describe the exact specifications of how methods and loops should operate in code. We’ll use these as the basis of unit tests in this course to help prove the correctness of data structures and algorithms we are asked to develop throughout the course.

In addition, we were introduced to the concepts of time complexity, space complexity, and code complexity, three ways to measure the performance and usefulness of a computer program. We also learned that it may be difficult to find a perfect program that has very little time, space, and code complexity, so many times we’ll have to consider a trade-off between programs that operate quickly, use less memory, and are easier to understand.

Which these tools, we’re in a much better place to understand the specifics of the data structures and algorithms we’ll encounter in this module. Next, we’ll do a short project to explore how we can build programs based on a set of preconditions, postconditions, and invariants instead of the plain language descriptions we’ve used up to this point.