Singly Linked Lists - Insertion
Given the structure of our linked list, we can easily insert a new node at any location in the list. However, for our purposes we are generally interested in inserting new nodes at the beginning of the list, at some specific location in the list, or in the appropriate order if the list is sorted.
Inserting at the Beginning
Inserting a node at the beginning of a list is straightforward. We just have to be careful about the order we use when swapping pointers. In the prepend code below, line 1 creates the new node to be stored in the list. Next, line 2 assigns the pointer in the new node to point to the pointer held by the head. If there was an item already in the list, head will point to the previous first item in the list. If the list was empty, head will have been null and thus the node.next will become null as well. Line 3 assigns head to point to the new node and line 4 increments our size variable.
function prepend(data)
node = new Node(data) (1)
node.next = head (2)
head = node (3)
size = size + 1 (4)
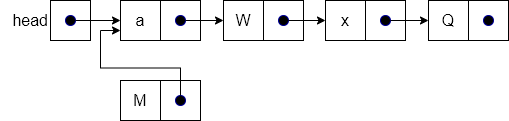
end functionWe show this process in the following example. The figure below shows the initial state as we enter the prepend operation. Our list has three items in it, an “a”, “W”, and “Q” and we want to add the new node “M” in front of item “a”.
The figure below shows the effect of the first step of the operation. This step creates a new node for “M” and changes next to point at the same node as the pointer held by head, which is the address of the first item in the list, “a”.
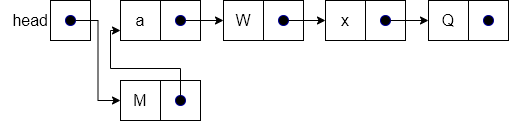
The result of performing line 3 in the operation is shown below. In line 3 we simply change head to point to our new node, instead of node “a”. Notice now that the new node has been fully inserted into the list.
And, if we redraw our diagram a bit, we get a nice neat list!
Since there are no loops in the prepend operation, prepend runs in constant time.
Inserting in the Middle
Inserting a node at a given index in the linked list is a little more difficult than inserting a node at the beginning of the list. First, we have to find the proper location to insert the new node before we can actually insert it. However, since we are given an index number, we simply need to follow the linked list to the appropriate index and then perform the insertion.
We do have a precondition to meet before we proceed, however. We need to make sure that the index provided to the operation is not less than 0 and that it is not greater than the size of the list, which is checked in line 2. If the precondition is not satisfied, we raise an exception in line 3.
function insertAt(data, index) (1)
if index < 0 or index > size (2)
raise exception (3)
elseif index == 0 (4)
prepend(data) (5)
else
curr = head.next (6)
prev = head (7)
node = new Node(data) (8)
for i = 1 to index – 1 (9)
prev = curr (10)
curr = curr.next (11)
end for (12)
prev.next = node (13)
node.next = curr (14)
size = size + 1 (15)
end if
end functionLines 4 and 5 check to see if the index is 0, which means that we want to insert it as the first item in the list. Since this is the same as the prepend operation we’ve already defined, we simply call that operation. While this may not seem like a big deal, it is actually more efficient and helps us to simplify the code in the rest of the operation.
The operation uses curr to keep track of which node in the list we are currently looking at, thus we initialize curr to point at the first node in the list in line 6. To allow us to swap pointers once we find the appropriate place in the list, we keep track of the node previous to curr as well by using the variable pre. This variable is initialized to head in line 7, and line 8 creates the new node we will insert into our list. After line 8, our list, node, and previous pointers would look like the following (assuming the index passed in was 2).
At this point we start our walk through the list using the for loop in lines 9 - 12. Specifically, with an index of 2 we will actually go through the loop exactly one time, from 1 to 1. Each time through the loop, lines 10 and 11 will cause curr and prev to point at the next nodes in the list. At the end of one time through our loop, our example will be as shown below.
Now, the only thing left to do is update the next pointer of node “3” to point at node (line 13), and node.next to point at curr node (line 14), while line 15 increments the size attribute. The updated list is shown below.
The insertAt operation, while being quite flexible and useful, can potentially loop through each node in the list. Therefore, it runs in order $N$ time.
Inserting in Order
When we want to insert an item into an ordered list, we need to find the right place in the list to actually insert the new node. Essentially, we need to search the list to find two adjacent nodes where the first node’s data is less than or equal to data and the second node’s data is greater than data. This process requires a linear search of the list.
function insertOrdered(data)
curr = head (1)
index = 0 (2)
while curr != NULL AND curr.data < data (3)
index = index + 1 (4)
curr = curr.next (5)
end while
insertAt(data, index) (6)
end functionNotice that we do not have a precondition since we will search the list for the appropriate place to insert the new node, even if the list is currently empty. In line 1, we create a curr variable to point to the current node we are checking in the list, while in line 2 we initialize an index variable to keep track of the index of curr in the list.
Next, lines 3 – 5 implement a loop that searches through the list to find a node where the data in that node is greater than or equal to the data we are trying to put into the list. We also check to see if we are at the end of the list. Inside the loop, we increment index and point curr to the next node in the list.
Once we find the appropriate place in the list, we simply call the insertAt operation to perform the actual insertion. Using the insertAt operation provides a nice, easy to understand operation. However, we do suffer a little in efficiency since both operations loop through the list to the location where we want to insert the new data node. However, since the insertAt call is not embedded within the loop, our insertOrdered operation still runs in order $N$ time.
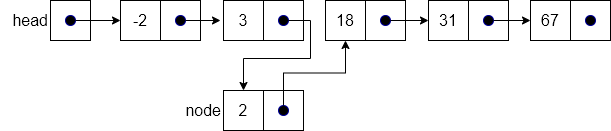
Since the previous example inserts the number 2 into the list (which falls between -1 and 3), the results of running the insertOrdered operation will be the same output as the result of the insertAt operation as shown above.