Memory Example
Consider the following block of pseudocode:
1. function APPENDER(NUMBER, BASE)
2. RESULT = ""
3. loop I from 1 to NUMBER
4. RESULT = RESULT + BASE
5. if I MOD 2 = 0
6. RESULT = RESULT + " "
7. else
8. RESULT = RESULT + ", "
9. end loop
10. return RESULT
11. end functionLets step through the function call with APPENDER(4,'abc') and analyze the memory that the code takes.
Recall that strings are reference variables. As such, string variables hold pointers to values and the value is stored in memory. For the following example, the HEAP refers to what is currently stored in memory and VARIABLE shows the current value of the variable RESULT.
-
Initialization: In line two, we initialize
RESULTas an empty string. In the heap, we have the empty string at memory location0x1. Thus,RESULTis holding the pointer0x1.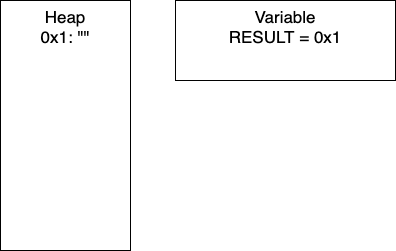

-
I = 1: Now we have entered the loop and on line 4, we add more characters to our string. At this point, we would have entry
0x2in our heap and our variableRESULTwould have the pointer0x2. Continuing through the code, line 5 determines ifIis divisible by 2. In this iterationI = 1, so we take the else branch. We again add characters to our string, resulting in a new entry in0x3and our variableRESULTcontaining the pointer0x3. In total, we have written 8 characters. We then incrementIand move to the next iteration.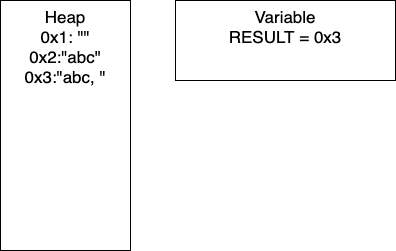

-
I = 2: We continue the loop and on line 4, we add more characters to our string. At this point, we would have entry
0x4in our heap and our variableRESULTwould have the pointer0x4. Continuing through the code, line 5 determines ifIis divisible by 2. In this iterationI = 2, so we take the if branch. We again add characters to our string, resulting in a new entry in0x5and our variableRESULTcontaining the pointer0x5. In this iteration, we have written 17 characters. We then incrementIand move to the next iteration of the loop.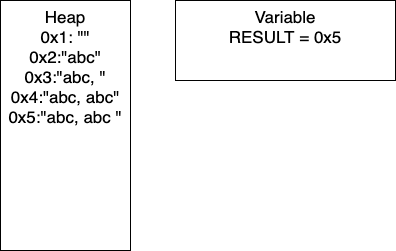

-
I = 3: We continue the loop and on line 4, we add more characters to our string. At this point, we would have entry
0x6in our heap and our variableRESULTwould have the pointer0x6. Continuing through the code, line 5 determines ifIis divisible by 2. In this iterationI = 3, so we take the if branch. We again add characters to our string, resulting in a new entry in0x7and our variableRESULTcontaining the pointer0x7. In this iteration, we have written 26 characters. We then incrementIand thusI = 4breaking out of the loop.

We can do some further analysis of the memory that is required for this particular block.
| Iteration | Memory Entries | Total Character Copies |
|---|---|---|
| 1 | 3 | 8 |
| 2 | 5 | 8 + 17 = 25 |
| 3 | 7 | 25 + 26 = 51 |
| 4 | 9 | 51 + 35 = 86 |
| . | . | . |
| n | 2n + 1 | (9n2 + 7n)/2 |
You need not worry about creating the equations! Based on this generalization, if the user wanted to do 100K iterations, say for gene sequencing, there would be (2x100,000 - 1) = 200,001 memory entries and (9x100,0002 + 7x100,000)/2 = 45 billion character copies. This behavior is not exclusive to strings; this will occur for any immutable type.
While this example is contrived, it is not too far off the mark. Another caveat to this analysis is that, depending on our programming language, there will be a periodic ‘memory collection’; there wont be 200K memory addresses occupied at one time. Writing to memory in this way can be costly in terms of time, which in industry is money.