Terms III
YouTube VideoWhen working with multidimensional data structures, we also need to consider how they would be stored in a linear manner. Remember, pieces of data in computers are linear sequences of binary digits. As a result, we need a standard way of storing trees as a linear structure.
-
Path- a path is a sequence of nodes and edges, which connect a node with its descendant. We can look at some paths in the tree above:- From
QtoO:QRO
From `Q` to `Y`:
`QWY`From `R` to `P`:
`RP` - From
-
Traversalis a general term we use to describe going through a tree. The following traversals are defined recursively.
Preorder Traversal
- Access the root, record its value.
- Run the preorder traversal each of the children
- The
Prerefers to the root, meaning the root goes before the children. - Remember: Root Children
- For the above tree, the preorder traversal could result in:
QWYUERIOPTA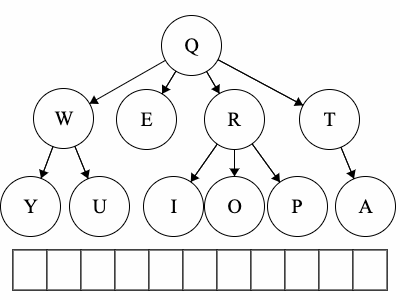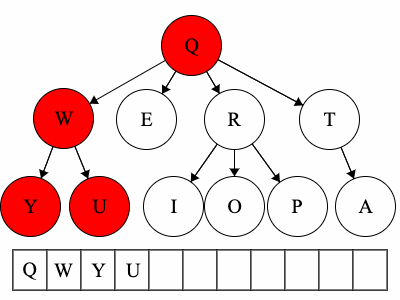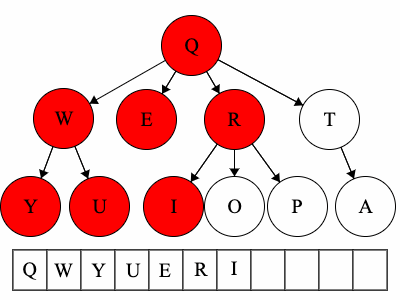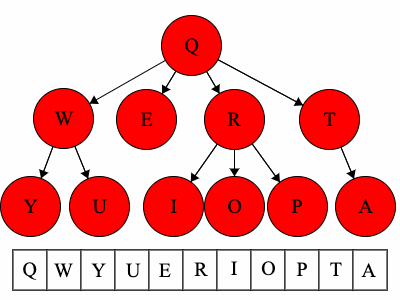

Postorder Traversal
- Run the postorder traversal on each of the children
- Access the root, record its value
- The
Postrefers to the root, meaning the root goes after the children. - Remember: Children Root
- For the above tree, the postorder traversal could result in:
YUWEIOPRATQ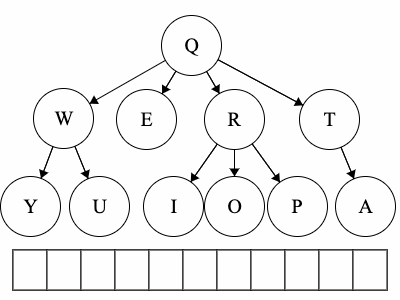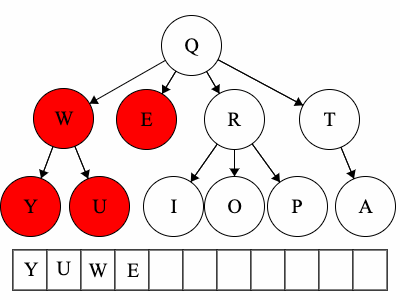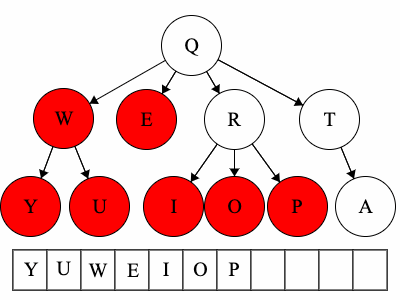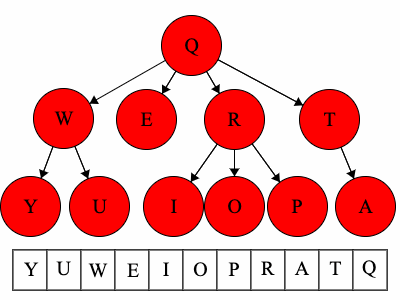

When we talk about traversals for general trees we have used the phrase ’the traversal could result in’. We would like to expand on why ‘could’ is used here. Each of these general trees are the same but their traversals could be different. The key concept in this is that for a general tree, the children are an unordered set of nodes; they do not have a defined or fixed order. The relationships that are fixed are the parent/child relationships.
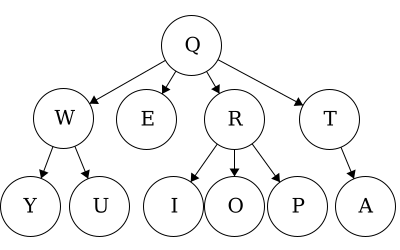

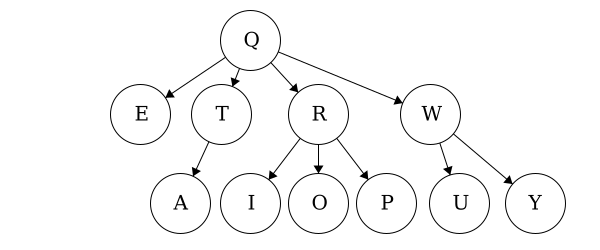

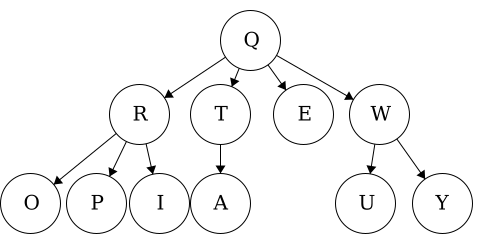

| Tree | Preorder | Postorder |
|---|---|---|
| Tree 1 | QWYUERIOPTA |
YUWEIOPRATQ |
| Tree 2 | QETARIOPWUY |
EATIOPRUYWQ |
| Tree 3 | QROPITAEWUY |
OPIRATEUYWQ |