Recall that in the beginning of our discussions about trees, we looked at a small tree which contained seven strings as motivation for trees. This was a small example of a trie (pronounced ’try’) which is a type of tree that can represent sets of words.

Tries can be used for a variety of tasks ranging from leisurely games to accessibility applications. One example is ‘Boggle’ where players have a set of random letters and try to make as many words as possible. To code this game, we could create a vocabulary with a trie then traverse it to determine if players have played legal words. We can also use tries to provide better typing accessibility. Users could type a few letters of a word and our code could traverse the trie and suggest what letters or words they may be trying to enter.

A trie is a type of tree with some special characteristics. First it must follow the guidelines of being a tree:

• There must be a single root,
• Each child node has a single parent node,
• It must be fully connected (no disjoint parts), and
• There can be no cycles (no loops).

The special characteristics for tries are:

• By starting at the root and traversing parent to children relationships we can build user-defined words, and
• Each node has a boolean property to indicate if it is the end of a word.

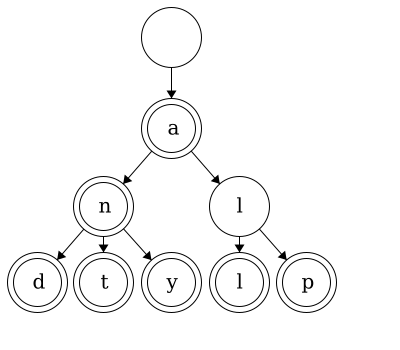
In this course, we will display nodes with two circles as a convention to show which nodes are the end of words. Looking at this small trie as an example, we can determine which words are contained in our trie. We start at the root, which will typically be an empty string, and traverse to a double lined node. "" -> a -> l -> l. Thus, the word ‘all’ is contained in our trie. Words within our tries do not have to end at leaves. For example, we can traverse "" -> a for the word ‘a’. We say this trie ‘contains’ seven words: ‘a’, ‘an’, ‘and’, ‘ant’, ‘any’, ‘all’, and ‘alp’.