Tries

Recall that in the beginning of our discussions about trees, we looked at a small tree which contained seven strings as motivation for trees. This was a small example of a trie (pronounced ’try’) which is a type of tree that can represent sets of words.

Tries can be used for a variety of tasks ranging from leisurely games to accessibility applications. One example is ‘Boggle’ where players have a set of random letters and try to make as many words as possible. To code this game, we could create a vocabulary with a trie then traverse it to determine if players have played legal words. We can also use tries to provide better typing accessibility. Users could type a few letters of a word and our code could traverse the trie and suggest what letters or words they may be trying to enter.

A trie is a type of tree with some special characteristics. First it must follow the guidelines of being a tree:

• There must be a single root,
• Each child node has a single parent node,
• It must be fully connected (no disjoint parts), and
• There can be no cycles (no loops).

The special characteristics for tries are:

• By starting at the root and traversing parent to children relationships we can build user-defined words, and
• Each node has a boolean property to indicate if it is the end of a word.

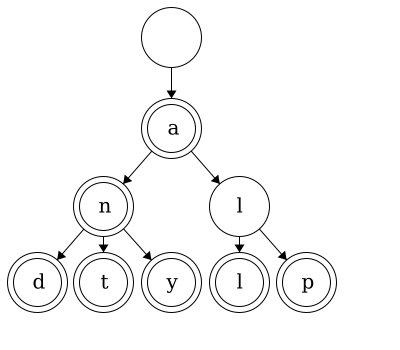
In this course, we will display nodes with two circles as a convention to show which nodes are the end of words. Looking at this small trie as an example, we can determine which words are contained in our trie. We start at the root, which will typically be an empty string, and traverse to a double lined node. "" -> a -> l -> l. Thus, the word ‘all’ is contained in our trie. Words within our tries do not have to end at leaves. For example, we can traverse "" -> a for the word ‘a’. We say this trie ‘contains’ seven words: ‘a’, ‘an’, ‘and’, ‘ant’, ‘any’, ‘all’, and ‘alp’.

Trie Example

Let’s look at another example of a trie. Here we have a larger trie. Think about how many words are captured by the tree; click the tree to see how many!

While the ‘a’, ‘at’, and ‘bee’ are words in the English language, they are not recognized by our trie. Depending on what the user intended, this could be by design. When we build our tries, users will input words that are valid for their vocabulary. Tries are not limited to the English language and can be created for any vocabulary.

MyTrie I

To implement our own trie, we will build off of MyTree that we built recursively. We will add an attribute to our tree to reinforce which nodes are words and which ones are not.

Attributes

We have the existing attributes of MyTree: parent, children, and item. For MyTrie, we introduce the boolean attribute is_word to delineate if our trie is a word.

Adding a Word

To add a word to our trie, we traverse through the trie letter by letter. We can define this recursively.

• Base Case: length of the word is zero and it was already a word in our trie, return false (because we did not add the word) OR length of the word is zero and it is not already a word in our trie, set the boolean for the node at the end of the word to true and return true
• Recursive case: split the string into the first character and the rest. Get the node of the first letter of the string; if it does not exist create it, then run the add word function on the remainder of the string.

function ADDWORD(WORD)
    if WORD length is 0
        if already a word
            return false
        else
            set is_word to true
            return true
    else
        FIRST = first character of WORD
        REMAIN = remainder of WORD
        CHILD = FINDCHILD(FIRST)
        if CHILD is NONE
            NODE = new MyTrie with item equal FIRST
            insert NODE into our existing trie 
            CHILD = NODE
        return CHILD.ADDWORD(REMAIN)
end function

Removing a Word

Similar to adding a word, we traverse our trie letter by letter. Once we get to the end of the word set is_word to false. If the word ends at a leaf, we will remove the leaf (then if the second to last character is a leaf, we remove the leaf and so on). If the word does not end in a leaf, meaning another word uses that node, we will not remove the node.

• Base Case: length of the word is zero and it was not a word in our trie, return false (because we did not remove the word) OR length of the word is zero and it is already a word in our trie, set the boolean for the node at the end of the word to false and return true
• Recursive case: split the string into the first character and the rest. Get the node of the first letter of the string, if that node does not exist, return false (because we did not remove the word). If the node does exist run remove word on the child for the remainder of the word. After that, if the node’s is_word is false and it is a leaf, remove the node.

function REMOVEWORD(WORD)
    if WORD length is 0
        if already not a word
            return false
        else
            set is_word to false
            return true
    else
        FIRST = first character of WORD
        REMAIN = remainder of WORD
        CHILD = FINDCHILD(FIRST)
        if CHILD is NONE
            return false
        else
            RET = CHILD.REMOVEWORD(REMAIN)
            if CHILD is not a word AND CHILD is a leaf
                REMOVECHILD(CHILD)
            return RET
end function

Check if trie contains word

Again, we will traverse the trie letter by letter. Once we get to the last letter, we can return that nodes is_word attribute. There is a chance that somewhere in our word, the letter is not a child of the previous node. If that is the case, then we return false.

function CONTAINSWORD(WORD)
    if WORD length is 0
        return `is_word`
    else
        FIRST = first character of WORD
        REMAIN = remainder of WORD
        CHILD = FINDCHILD(FIRST)
        if CHILD is NONE
            return false
        else
            return CHILD.CONTAINSWORD(REMAIN)
end function

MyTrie II

Getters

Getting word count

For this function, we want to get the total number of words that are contained within our trie. We will fan out through all of the children and count all of the nodes that have their is_word attribute equal to true.

function WORDCOUNT()
    COUNT = 0
    if is_word
        COUNT = 1
    for CHILD in CHILDREN
        COUNT += CHILD.WORDCOUNT()
    return COUNT
end function

Get max word length

Next, we want to get the longest word contained in our trie. To do this, we will recurse each child and find the maximum length of the child.

• Base Case: we are at a leaf and it is a word, return 0
• Recursive Case: declare a maximum of -1 for a tracker and then for each child run the maximum word length function on it. If the value returned from the child is greater than our maximum tracker, set the tracker equal to the value. Once we have iterated all of the children, return the maximum tracker plus one.

function MAXWORD()
    if LEAF and is_word
        return 0
    else
        MAX = -1
        for CHILD in CHILDREN
            COUNT = CHILD.MAXWORD()
            if COUNT greater than MAX
                MAX = COUNT
        return MAX + 1
end function

Get completions

This function will act as an auto-complete utility of sorts. A user will input a string of characters and we will return all of the possible words that are contained in our trie. This will happen in two phases. First, we traverse the trie to get to the end of the input string (lines 1-12). The second portion then gets all of the words that are contained after that point in our trie (lines 14-21).

function COMPLETIONS(WORD)
1.    if WORD length greater than 0
2.        FIRST = first character of WORD
3.        REMAIN = remainder of WORD
4.        CHILD = FINDCHILD(FIRST)
5.        if CHILD is none
6.            return []
7.        else
8.            COMPLETES = CHILD.COMPLETIONS(REMAIN)
9.            OUTPUT = []
10.            for COM in COMPLETES
11.                append CHILD.item + COM to OUTPUT
12.            return OUTPUT
13.    else
14.        OUTPUT = []
15.        if is_word
16.            append ITEM to OUTPUT
17.        for CHILD in CHILDREN
18.            COMPLETES = CHILD.COMPLETIONS("")
19.            for COM in COMPLETES
20.                append CHILD.item + COM to OUTPUT
21.        reutrn OUTPUT
end function