In the first module we discussed two types of traversals: preorder and postorder. Within that discussion, we noted that for general trees, the preorder and postorder traversal may not be unique. This was due to the fact that children nodes are an unordered set.
Info
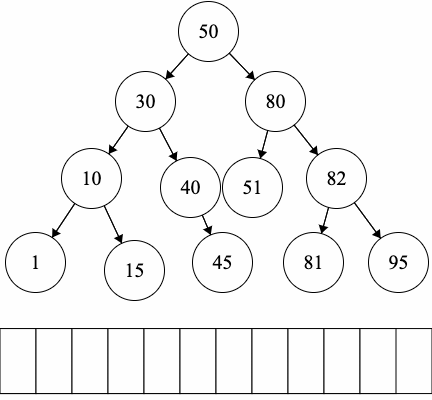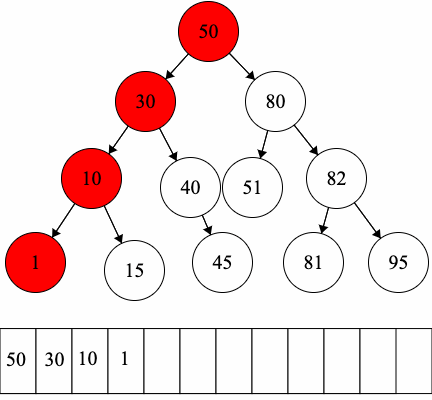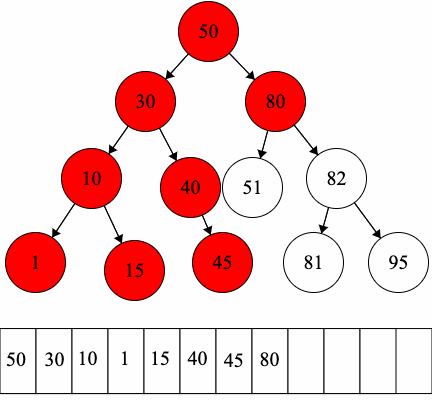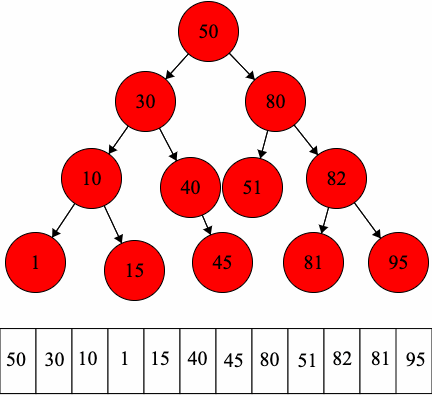
We are now working with binary trees which have a defined child order. As a result, the preorder and postorder traversals will be unique! These means that for a binary tree when we do a preorder traversal there is exactly one string that is possible. The same applies for postorder traversals as well.
Recall that these were defined as such:
- Preorder Traversal (Remember: Root Children):
- Access the root
- Run the preorder traversal on the children
- Postorder Traversal (Remember: Children Root):
- Run the postorder traversal on the children
- Access the root.
Now for binary trees, we can modify their definitions to be more explicit:
- Preorder Traversal (Remember: Root Left Right):
- Access the root
- Run the preorder traversal on the left child
- Run the preorder traversal on the right child
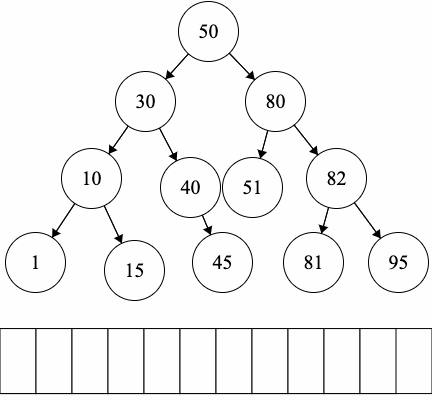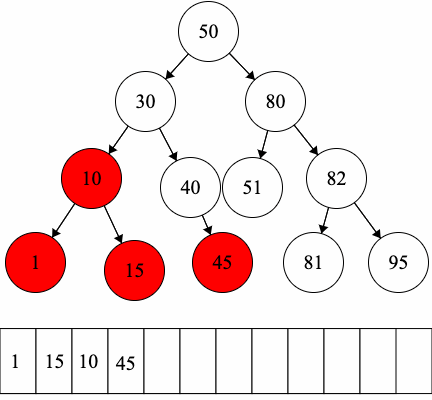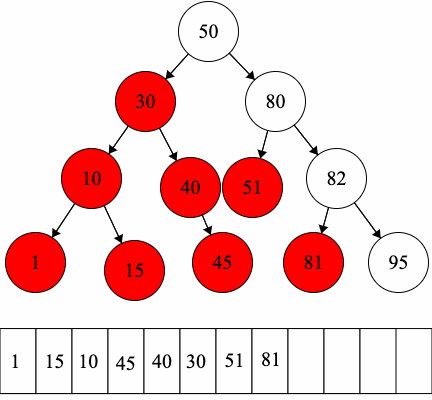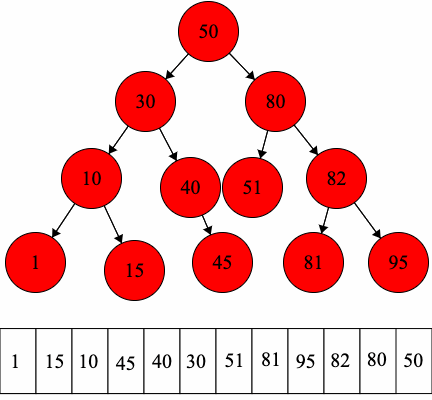
- Postorder Traversal (Remember: Left Right Root):
- Run the postorder traversal on the left child
- Run the postorder traversal on the right child
- Access the root.
Let’s practice traversals on the following binary tree.