Binary Trees
Welcome!
This page is the main page for Binary Trees
This page is the main page for Binary Trees
A binary tree is a type of tree with some special conditions. First, it must follow the guidelines of being a tree:
The special conditions that we impose on binary trees are the following:
To reinforce these concepts, we will look at examples of binary trees and examples that are not binary trees.

 This is a valid binary tree. We have a single node, the root, with no children. As with general trees, binary trees are built recursively. Thus, each node and its child(ren) are trees themselves.
This is a valid binary tree. We have a single node, the root, with no children. As with general trees, binary trees are built recursively. Thus, each node and its child(ren) are trees themselves.
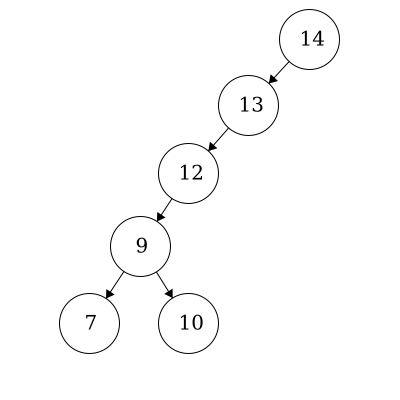
 This is also a valid binary tree. All of the left children are less than their parent. The node with item ‘10’ is also in the correct position as it is less than 12, 13, and 14 but greater than 9.
This is also a valid binary tree. All of the left children are less than their parent. The node with item ‘10’ is also in the correct position as it is less than 12, 13, and 14 but greater than 9.
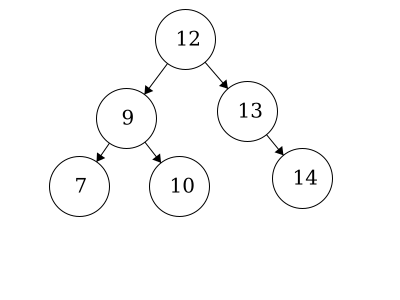
 We have the same nodes but our root is now 12 whereas before it was 14. This is also a valid binary tree.
We have the same nodes but our root is now 12 whereas before it was 14. This is also a valid binary tree.
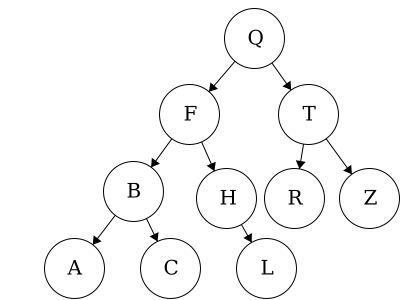
 Here we have an example of a binary tree with alphabetical items. As long as we have items which have a predefined order, we can organize them using a binary tree.
Here we have an example of a binary tree with alphabetical items. As long as we have items which have a predefined order, we can organize them using a binary tree.
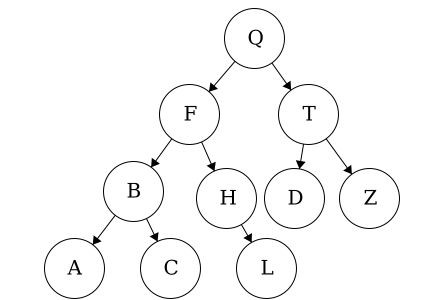
 We may be inclined to say that this is a binary tree: each node has 0, 1, or 2 children and amongst children and parent nodes, the left child is smaller than the parent and the right child is greater than the parent. However, in binary trees, all of the nodes in the left tree must be smaller than the root and all of the nodes in the right tree must be larger than the root. In this tree,
We may be inclined to say that this is a binary tree: each node has 0, 1, or 2 children and amongst children and parent nodes, the left child is smaller than the parent and the right child is greater than the parent. However, in binary trees, all of the nodes in the left tree must be smaller than the root and all of the nodes in the right tree must be larger than the root. In this tree, D is out of place. Node D is less than node T but it is also less than node Q. Thus, node D must be on the right of node Q.
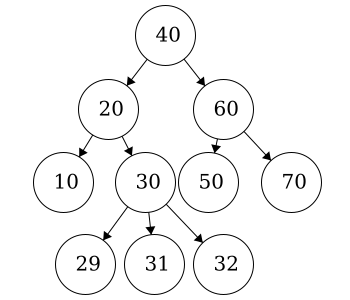
 In this case, we do not have a binary tree. This does fit all of the criteria for being a tree but not the criteria for a binary tree. Nodes in binary trees can have at most 2 children. Node
In this case, we do not have a binary tree. This does fit all of the criteria for being a tree but not the criteria for a binary tree. Nodes in binary trees can have at most 2 children. Node 30 has three children.
In the first module we discussed two types of traversals: preorder and postorder. Within that discussion, we noted that for general trees, the preorder and postorder traversal may not be unique. This was due to the fact that children nodes are an unordered set.
We are now working with binary trees which have a defined child order. As a result, the preorder and postorder traversals will be unique! These means that for a binary tree when we do a preorder traversal there is exactly one string that is possible. The same applies for postorder traversals as well.
Recall that these were defined as such:
Now for binary trees, we can modify their definitions to be more explicit:
Let’s practice traversals on the following binary tree.
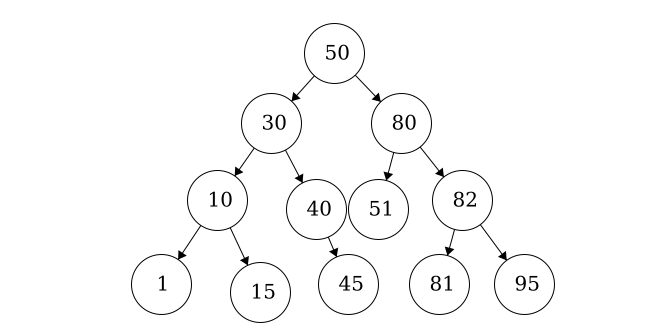

Since we have fixed order on the children, we can introduce another type of traversal: in-order traversal.
In-order Traversal:
Our implementation of binary trees will inherit from our MyTree implementation as binary trees are types of trees. Thus, MyBinaryTree will have the functionality of MyTree in addition to the following.
The binary tree has two attributes
MyBinaryTree, the item should be less than the item of the parent.MyBinaryTree, the item should be greater than the item of the parent.Get Size
MyTree size function. If the tree is empty then we return zero. If the tree is not empty then call the MyTree size function.Is Empty
To Sorted List
function TOSORTEDLIST()
LIST = []
if there`s LEFTCHILD
LIST = LIST + LEFTCHILD.TOSORTEDLIST
LIST = LIST + ITEM
if there`s RIGHTCHILD
LIST = LIST + RIGHTCHILD.TOSORTEDLIST
return LISTWhen inserting children to a binary tree, we must take some special considerations. All of the node items in the left tree must be less than the parent node item and all of the node items in the right tree must be greater than the parent node item.
The general procedure for adding a child is the following:
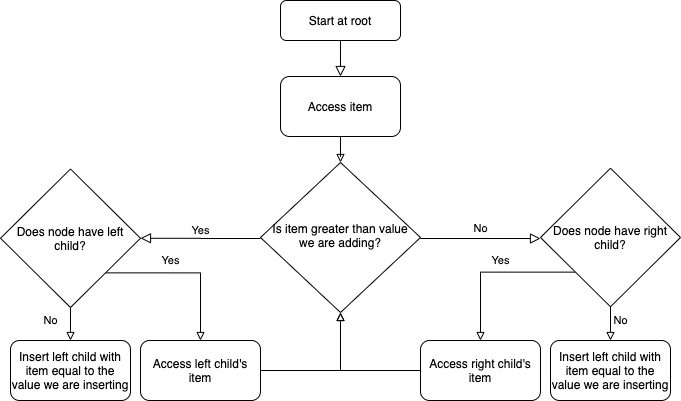

Suppose that we have the following tree and we want to add a node with item ‘85’. Click the binary tree to see the resulting tree.
function INSERT(VALUE)
if node is empty:
set nodes item to value
else:
if node.ITEM is VALUE
return false
else if node.ITEM > VALUE
LC = node`s left child
if LC is NONE
CHILD = new BINARYTREE with root.ITEM equal VALUE
add CHILD to nodes children
set node.LEFTCHILD equal to CHILD
return true
else
return LC.INSERT(VALUE)
else
RC = node`s right child
if RC is NONE
CHILD = new BINARYTREE with root.ITEM equal VALUE
add CHILD to nodes children
set node.RIGHTCHILD equal to CHILD
return true
else
return RC.INSERT(VALUE)
end functionRemoving children is not as straightforward as inserting them. The general procedure for removing a child is to replace that nodes value with its smallest right descendant. First we will traverse the binary tree until we find the node with the value we are trying to remove (lines 18-32 below). Then we have three separate cases, discussed in detail below.
Removing a leaf is the most straightforward. We remove the value from the node and then sever the connection between parent and child. (lines 5-7 below)
Suppose we have this binary tree and we want to remove value 5. What do you think the resulting binary tree will look like? Click the binary tree to see the result.
When we remove a value from a node that does not have a right child, we cannot replace the value with the smallest right child. In this instance we will instead replace the value with the smallest left child then prune the tree to clean it up. Once we replace the value, we must switch the node’s left child to be the right child in order to maintain proper binary tree structure. (lines 8-13 below)
Suppose we have this binary tree and we want to remove value 4. What do you think the resulting binary tree will look like? Click the binary tree to see the result.
When we remove a value from a node that has a right child, we can replace the value with the nodes smallest right child. (Lines 14-17 Below)
Suppose we have this binary tree and we want to remove value 10. What do you think the resulting binary tree will look like? Click the binary tree to see the result.
1. function REMOVE(VALUE)
2. if node is empty:
3. error
4. if node.ITEM is VALUE
5. if node is a leaf
6. set node.ITEM to none
7. return TRUE
8. else if node has no right child
9. node.ITEM = LEFTCHILD.REMOVESMALLEST()
10. prune left-side
11. store left child in right child
12. set left child to none
13. return TRUE
14. else
15. node.ITEM = RIGHTCHILD.REMOVESMALLEST()
16. prune right-side
17. return TRUE
18. else
19. if node.ITEM > VALUE
20. if node has LEFTCHILD
21. SUCCESS = LEFTCHILD.REMOVE(VALUE)
22. prune left-side
23. return SUCCESS
24. else
25. return FALSE
26. else
27. if node has RIGHTCHILD
28. SUCCESS = RIGHTCHILD.REMOVE(VALUE)
29. prune right-side
30. return SUCCESS
31. else
32. return FALSE
33. end functionWe use the pruning functions to severe the tie between parent and child nodes.
function PRUNERIGHT()
if RIGHTCHILD has no value
REMOVECHILD(RIGHTCHILD)
set this nodes RIGHTCHILD former RIGHTCHILDs RIGHTCHILD
if RIGHTCHLID is not none
ADDCHILD(RIGHTCHILD)
end functionfunction PRUNELEFT()
if LEFTCHILD has no value
REMOVECHILD(LEFTCHILD)
set this nodes LEFTCHILD former LEFTCHILDs RIGHTCHILD
if LEFTCHILD is not none
ADDCHILD(LEFTCHILD)
end functionWe use the remove smallest function to retrieve the smallest value in the binary tree which will replace our value.
function REMOVESMALLEST()
if node has left child
REPLACEMENT = LEFTCHILD.REMOVESMALLEST
prune left-side
return REPLACEMENT
else
REPLACEMENT = node.ITEM
if node has right child
node.ITEM = RIGHTCHILD.REMOVESMALLEST()
prune right-side
else
node.ITEM = NONE
return REPLACEMENT
end function
 While this is a valid binary tree, it is not balanced. Let’s look at the following tree.
While this is a valid binary tree, it is not balanced. Let’s look at the following tree.

 We have the same nodes but our root is now 12 whereas before it was 14. This is a valid binary tree. We call this a
We have the same nodes but our root is now 12 whereas before it was 14. This is a valid binary tree. We call this a balanced binary tree. A balanced binary tree looks visually even amongst the left and right trees in terms of number of nodes.
Note: Balancing is not necessary for a valid binary tree. It is, however, important in terms of time efficiency to have a balanced tree. For example, the number of actions when inserting an element is about the same as the number of levels in the tree. If we tried to add the value 11 into the unbalanced tree, we would traverse 5 nodes. If we tried to add the value 11 in to the balanced tree, we would traverse just 3 nodes.
We believe that balancing binary trees is out of the scope of this course. If you are interested in how we might balance a tree, feel free to check out these videos by Dr. Joshua Weese.
YouTube Video YouTube Video