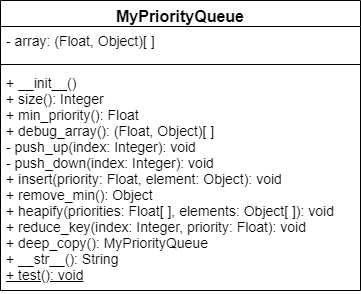
Attributes

The priority queue will have a single attribute which will be the array to represent the priority queue as a heap. Elements of this array will be ordered pairs where the first entry is the priority and the second entry is the node item.

Size

Similar to graphs, heaps will have a size which will be the number of elements currently in our heap.

Push

The PUSHDOWN and PUSHUP functions will help us to maintain the heap structure. In their own ways, described below, they will correct the ordering of nodes. Primarily making it such that the parent is always smaller then its children. Both of these will be recursive functions.

• PUSHUP: This function takes an index as input and then determines if the element at that index has a lower priority than its parent. This will ‘raise’ the element up through heap and move it closer to the front of the array.
  • Base Case: There are two base cases for PUSHUP. The first is if the element has greater priority than its parent, then we do nothing as the structure is correct. The second is if the index of the parent node is 0, then we do nothing as we have reached the root of the heap.
  • Recursive Case: When we are not at the root and the child has lower priority than the parent, then we will swap the parent element and the child element in the priority queue’s array. Then we will call the PUSHUP function with the parent index as input.
• PUSHDOWN: Similar to PUSHUP this function will take an index as input but will now determine if the node has higher priority than one of its children. This will ’trickle’ the element down through the heap and move it closer to the end of the array.
  • Base Case: There are two cases for PUSHDOWN. The first is if the the parent has lower priority than both of its children, then we do nothing as the structure is correct. The second is if the index of both children are out of the range of our array, then we do nothing as we have reached a leaf.
  • Recursive Case: When we are not at a leaf and at least one child has lower priority than the parent, then we will recurse. We will break this down into further cases for clarity.
    • Parent has a Right Child: If the priority of the left child is less than the priority of the right child, then we check the priority of the left child compared to the parent. If the left child has lower priority than the parent, then we swap the parent and the left child in the array and recurse on the left child. If the priority of the left child is not less than the priority of the right child, then we check the priority of the right child compared to the parent. If the right child has lower priority than the parent, then we swap the parent and the right child in the array and recurse on the right child.
    • Parent only has a Left Child: If the priority of the left child is less than the parent’s priority, then swap the left child and the parent in the array and then recurse on the left child.

Remove Min

This will remove the lowest priority element from our priority queue. If our priority queue only has one element, then we will just remove the element. However, if there is more than the single element, we will need to do some maintenance to make sure the lowest priority element is the root again. To do this, we will take the last element of the priority queue and make it the root. Then we will use the PUSHDOWN function to reorder the nodes.

Heapify

The HEAPIFY function will allow us to translate our data into a heap. It will take as input a list of priorities and a list of items. Suppose in the figure below, we are calling Prim’s function from node 1. Thus, we want to start our heap with the outgoing edges of node 1. We will input the list of priorities, which in this case are the edge weights, and the list of the items. For this application, we have made the items ordered pairs where the first entry is the source node and the second is the target.

Since we are working primarily with min-priority queues, we will define HEAPIFY in those terms. Though, we could have an equivalent function for a max-priority queue.

For input, the function takes RANKS which is the array representation of our priority values and ITEMS which is the array representation of the items.

function HEAPIFY(RANKS, ITEMS)
    if RANKS and ITEMS are the same size
        SIZE = length of ITEMS
        loop INDEX starting at 1 to SIZE
            I_RANK = value at INDEX in RANKS
            I_ITEM = item at INDEX of ITEMS 
            append (I_RANK, I_ITEM) to priority queues array
        QSIZE = length of our PQ - 1
        LASTPARENT = floor(QSIZE/2) + 1
        loop NODE starting at LASTPARENT down to 1
            PUSHDOWN(NODE)
    else
        error

Insert

The INSERT function is similar to HEAPIFY but now we are just wanting to insert a single element. As such, INSERT will take the priority of the element and the element as input. We will append the ordered pair of (priority, element) to our priority queue array and then call the PUSHUP function on the last element of the array.

Heap Decrease Key

The DECREASEKEY function allows us to update the priority of an element. It takes as input the array index for heap entry to update as well as the priority we will be giving the element. We first check if that the new priority is in fact less than the original. Then we update the priority and then push the element up.

DECREASEKEY(IDX, PRIORITY)
    ELEMENT = entry in array at IDX
    if PRIORITY > ELEMENT[0]
        error
    ELEMENT[0] = PRIORITY 
    PUSHUP(IDX)