Dijkstras

A good application of priority queues is finding the shortest path in a graph. A common algorithm for this is Dijkstra’s algorithm.

Edsger Dijkstra was a Dutch computer scientist who researched many fields. He is credited for his work in physics, programming, software engineering, and as a systems scientist. His motivation for this algorithm in particular was to be able to find the shortest path between two cities.

Info

“What is the shortest way to travel from Rotterdam to Groningen, in general: from given city to given city? It is the algorithm for the shortest path, which I designed in about twenty minutes. One morning I was shopping in Amsterdam with my young fiancée, and tired, we sat down on the café terrace to drink a cup of coffee and I was just thinking about whether I could do this, and I then designed the algorithm for the shortest path.” - Edsger Dijkstra, Communications of the ACM 53 (8), 2001.

His original algorithm was defined for a path between two specific cities. Since its publication, modifications have been made to the algorithm to find the shortest path to every node given a source node.

DIJKSTRAS(GRAPH, SRC)
    SIZE = size of GRAPH
    DISTS = array with length equal to SIZE
    PREVIOUS = array with length equal to SIZE
    set all of the entries in PREVIOUS to none
    set all of the entries in DISTS to infinity 

    DISTS[SRC] = 0 
    PQ = min-priority queue

    loop IDX starting at 0 up to SIZE
        insert (DISTS[IDX],IDX) into PQ

    while PQ is not empty
        MIN = REMOVE-MIN from PQ
        for NODE in neighbors of MIN
            WEIGHT = graph weight between MIN and NODE
            CALC = DISTS[MIN] + WEIGHT
            if CALC < DISTS[NODE]
                DISTS[NODE] = CALC
                PREVIOUS[NODE] = MIN
                PQIDX = index of NODE in PQ
                PQ decrease-key (PQIDX, CALC)
    return DISTS and PREVIOUS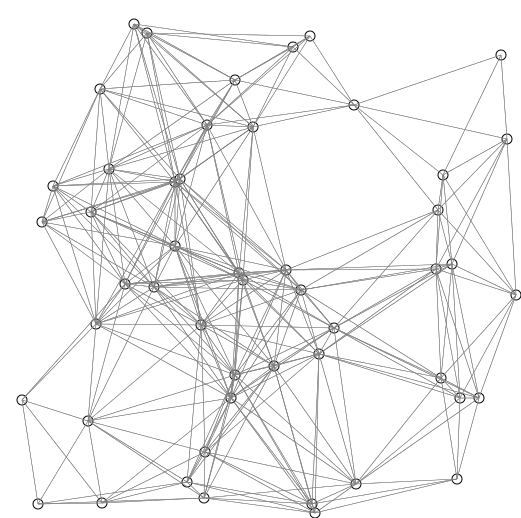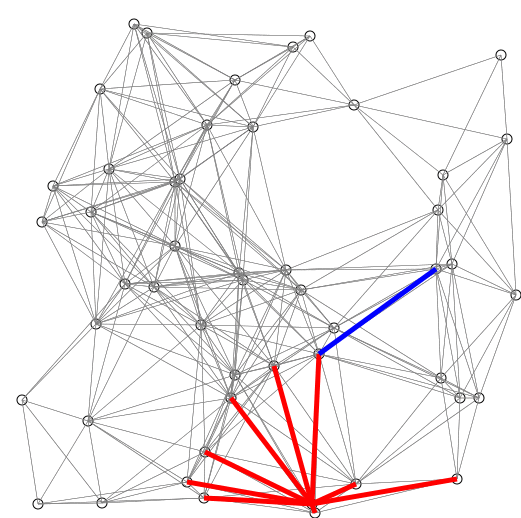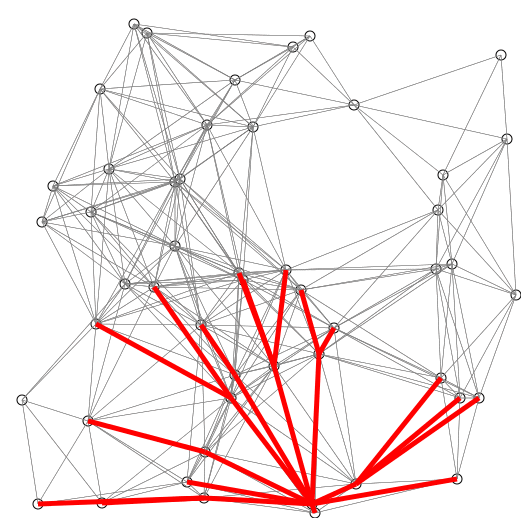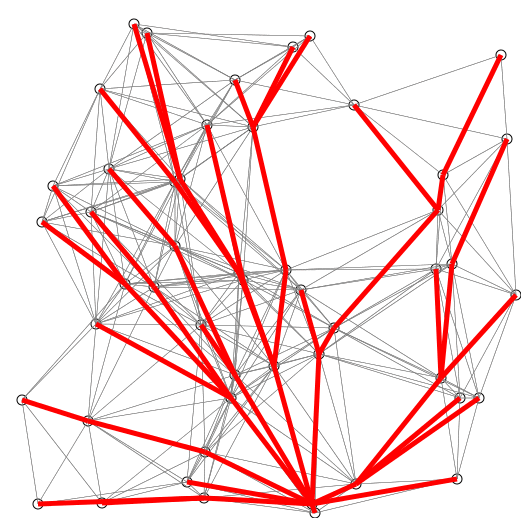

^[Shiyu Ji, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons, https://upload.wikimedia.org/wikipedia/commons/e/e4/DijkstraDemo.gif]

Aside from just finding routes for us to travel, Dijkstra’s algorithm can accommodate for any application that can have an abstraction to finding the shortest path. For example, the following animation shows how a robot could utilize Dijkstra’s algorithm to find the shortest path with an obstacle in the way. In this example, each node could represent one square foot of floor space and the edges would represent those spaces that are adjacent. In this scenario, we would most likely not have an associated edge weight. If the robot were traversing on a rugged terrain, then we could have the weights represent the difficultly of passing through the terrain from one space to the other. ^[Subh83, CC BY 3.0 https://creativecommons.org/licenses/by/3.0, via Wikimedia Commons, https://commons.wikimedia.org/wiki/File:Dijkstras_progress_animation.gif]

Another practical abstraction is in network routing. In this simplified abstraction, nodes would be routers or switches and the edges would be the physical links between them. The edge weights in this case would be the cost of sending a packet from one router to the next. Dijkstra’s algorithm is actively used in protocols such as Intermediate System to Intermediate System (IS-IS) and Open Shortest Path First (OSPF).