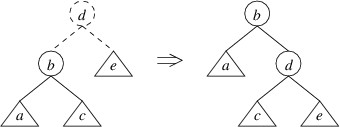
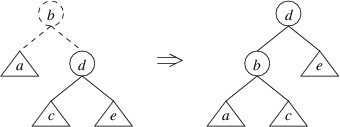
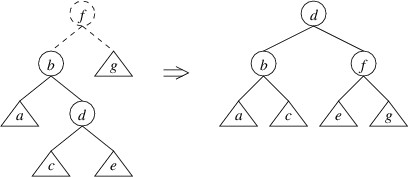
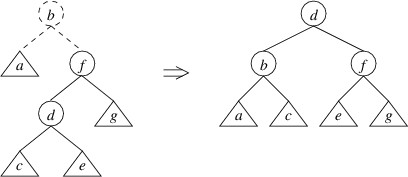
Subsections of C# Syntax
Reference Types and Value Types
Reference Types and Value Types
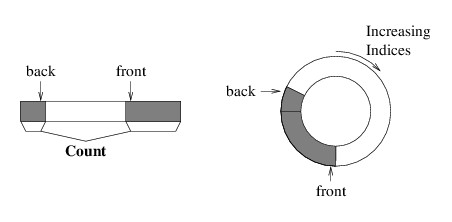
Data types in C# come in two distinct flavors: value types and reference types. In order to understand the distinction, it helps to consider how space is allocated in C#. Whenever a method is called, the space needed to execute that method is allocated from a data structure known as the call stack. The space for a method includes its local variables, including its parameters (except for out or ref parameters). The organization of the call stack is shown in the following figure:


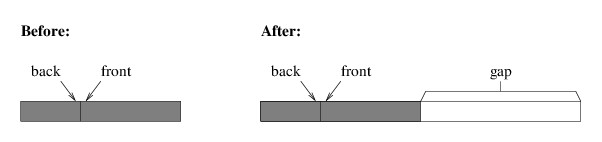
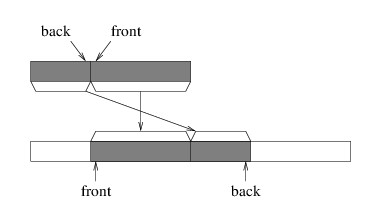
When the currently-running method makes a method call, space for that method is taken from the beginning of the unused stack space. When the currently-running method returns, its space is returned to the unused space. Thus, the call stack works like the array-based implementation of a stack, and this storage allocation is quite efficient.
What is stored in the space allocated for a variable depends on whether the variable is for a value type or a reference type. For a value type, the value of the variable is stored directly in the space allocated for it. There are two kinds of value types: structures and enumerations. Examples of structures include numeric types such as int, double, and char. An example of an enumeration is DialogResult (see "MessageBoxes" and “File Dialogs”).
Because value types are stored directly in variables, whenever a value is assigned to a variable of a value type, the entire value must be written to the variable. For performance reasons, value types therefore should be fairly small.
For reference types, the values are not stored directly into the space allocated for the variable. Instead, the variable stores a reference, which is like an address where the value of the variable can actually be found. When a reference type is constructed with a new expression, space for that instance is allocated from a large data structure called the heap (which is unrelated to a heap used to implement a priority queue). Essentially, the heap is a large pool of available memory from which space of different sizes may be allocated at any time. We will not go into detail about how the heap is implemented, but suffice it to say that it is more complicated and less efficient than the stack. When space for a reference type is allocated from the heap, a reference to that space is stored in the variable. Larger data types are more efficiently implemented as reference types because an assignment to a variable of a reference type only needs to write a reference, not the entire data value.
There are three kinds of reference types: classes, interfaces, records, and delegates. Records and delegates are beyond the scope of this course.
Variables of a reference type do not need to refer to any data value. In this case, they store a value of null (variables of a value type cannot store null). Any attempt to access a method, property, or other member of a null or to apply an index to it will result in a NullReferenceException.
The fields of classes or structures are stored in a similar way, depending on whether the field is a value type or a reference type. If it is a value type, the value is stored directly in the field, regardless of whether that field belongs to an object allocated from the stack or the heap. If it is a reference type, it stores either null or a reference to an object allocated from the heap.
The difference between value types and reference types can be illustrated with the following code example:
private int[] DoSomething(int i, int j)
{
Point a = new(i, j);
Point b = a;
a.X = i + j;
int[] c = new int[10];
int[] d = c;
c[0] = b.X;
return d;
}
Suppose this method is called as follows:
int[] values = DoSomething(1, 2);
The method contains six local variables: i, j, a, b, c, and d. int is a structure, and hence a value type. Point is a structure (and hence a value type) containing public int properties X and Y, each of which can be read or modified. int[ ], however, is a reference type. Space for all six of these variables is allocated from the stack, and the space for the two Points includes space to store two int fields for each. The values 1 and 2 passed for i and j, respectively, are stored directly in these variables.
The constructor in the first line of the method above sets the X property of a to 1 and the Y property of a to 2. The next statement simply copies the value of a - i.e., the point (1, 2) - to b. Thus, when the X property of a is then changed to 3, b is unchanged - it still contains the point (1, 2).
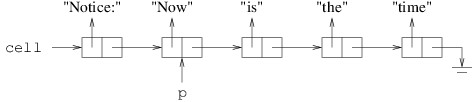
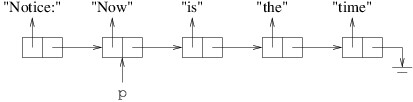
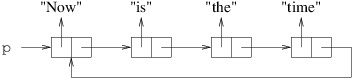
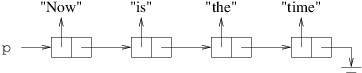
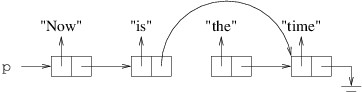
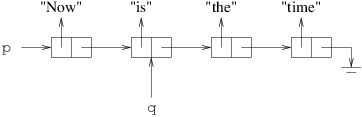
On the other hand, consider what happens when something similar is done with array variables. When c is constructed, it is assigned a new array allocated from the heap and containing 10 locations. These 10 locations are automatically initialized to 0. However, because an array is a reference type, the variable c contains a reference to the actual array object, not the array itself. Thus, when c is copied to d, the array itself is not copied - the reference to the array is copied. Consequently, d and c now refer to the same array object, not two different arrays that look the same. Hence, after we assign c[0] a value of 1, d[0] will also contain a value of 1 because c and d refer to the same array object. (If we want c and d to refer to different array objects, we need to construct a new array for each variable and make sure each location of each array contains the value we want.) The array returned therefore resides on the heap, and contains 1 at index 0, and 0 at each of its other nine locations. The six local variables are returned to unused stack space; however, because the array was allocated from the heap, the calling code may continue to use it.
It is sometimes convenient to be able to store a null in a variable of a value type. For example, we may want to indicate that an int variable contains no meaningful value. In some cases, we can reserve a specific int value for this purpose, but in other cases, there may be no int value that does not have some other meaning within the context. In such cases, we can use the ? operator to define a nullable version of a value type; e.g.,
We can do this with any value type. Nullable value types such as int? are the only value types that can store null.
Beginning with C# version 8.0, similar annotations using the ? operator are allowed for reference types. In contrast to its use with value types, this operator has no effect on the code execution when it is used with a reference type. Instead, such annotations are used to help programmers to avoid NullReferenceExceptions. For example, the type string is used for variables that should never be null, but string? is used for variables that might be null. Assigning null to a string variable will not throw an exception (though it might lead to a NullReferenceException later); however, starting with .NET 6, the compiler will generate a warning whenever it cannot determine that a value assigned to a non-nullable variable is not null. One way to avoid this warning is to use the nullable version of the type; e.g.,
The compiler uses a technique called static analysis to try to determine whether a value assigned to a variable of a non-nullable reference type is non-null. This technique is limited, resulting in many cases in which the value assigned cannot be null, but the compiler gives a warning anyway. (This technique is especially limited in its ability to analyze arrays.) In such cases, the null-forgiving operator ! can be used to remove the warning. Whenever you use this operator, the CIS 300 style requirements specify that you must include a comment explaining why the value assigned cannot be null (see “Comments”).
For example, a StreamReader’s ReadLine method returns null when there are no more lines left in the stream, but otherwise returns a non-null string (see “Advanced Text File I/O”). We can use the StreamReader’s EndOfStream property to determine whether all lines have been read; for example, if input is a StreamReader:
while (!input.EndOfStream)
{
string line = input.ReadLine();
// Process the line
}
However, because ReadLine has a return type of string? and the type of line is string, the compiler generates a warning - even though ReadLine will never return null in this context. We can eliminate the warning as follows:
while (!input.EndOfStream)
{
// Because input is not at the end of the stream, ReadLine won't return null.
string line = input.ReadLine()!;
// Process the line
}
Because classes are reference types, it is possible for the definition of a class C to contain one or more fields of type C or, more typically, type C?; for example:
public class C
{
private C? _nextC;
. . .
}
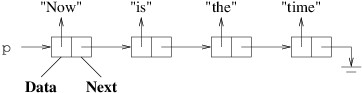
Such circularity would be impossible for a value type because there would not be room for anything else if we tried to include a value of type C? within a value of type C. However, because C is a class, and hence a reference type, _nextC simply contains either null or a reference to some object of type C. When the runtime system constructs an instance of type C, it just needs to make it large enough to hold a reference, along with any other fields defined within C. Such recursive definitions are a powerful way to link together many instances of a type. See “Linked Lists” and “Trees” for more information.
Because all types in C# are subtypes of object, which is a reference type, every value type is a subtype of at least one reference type (however, value types cannot themselves have subtypes). It is therefore possible to assign an instance of a value type to a variable of a reference type; for example:
When this is done, a boxed version of the value type is constructed,
and the value copied to it. The boxed version of the value type is
just like the original value type, except that it is allocated from
the heap and accessed by reference, not by value. A reference to this boxed version is then assigned to the variable of the reference type. Note that multiple variables of the reference type may refer to the same boxed instance of the value type.
Note also that boxing may also occur when passing parameters. For example, suppose we have a method:
private object F(object x)
{
}
If we call F with a parameter of 3, then 3 will need to be copied to a boxed int, and a reference to this boxed int will be assigned to x within F.
Enumerations
Enumerations
An enumeration is a value type containing a set of named constants. An example of an enumeration is DialogResult (see "MessageBoxes" and “File Dialogs”). The DialogResult type contains the following members:
- DialogResult.Abort
- DialogResult.Cancel
- DialogResult.Ignore
- DialogResult.No
- DialogResult.None
- DialogResult.OK
- DialogResult.Retry
- DialogResult.Yes
Each of the above members has a different constant value. In many cases, we are not interested in the specific value of a given member. Instead, we are often only interested in whether two expressions of this type have the same value. For example, the following code fragment is given in the "MessageBoxes" section:
DialogResult result = MessageBox.Show("The file is not saved. Really quit?", "Confirm Quit", MessageBoxButtons.YesNo);
if (result == DialogResult.Yes)
{
Application.Exit();
}
In the if-statement above, we are only interested in whether the user closed the MessageBox with the “Yes” button; i.e., we want to know whether the Show method returned the same value as DialogResult.Yes. For this purpose, we don’t need to know anything about the value of DialogResult.Yes or any of the other DialogResult members.
However, there are times when it is useful to know that the values in an enumeration are always integers. Using a cast, we can assign a member of an enumeration to an int variable or otherwise use it as we would an int; for example, after the code fragment above, we can write:
As a more involved example, we can loop through the values of an enumeration:
for (DialogResult r = 0; (int)r < 8; r++)
{
MessageBox.Show(r.ToString());
}
The above loop will display 8 MessageBoxes in sequence, each displaying the name of a member of the enumeration (i.e., “None”, “OK”, etc.).
Variables of an enumeration type may be assigned any value of the enumeration’s underlying type (usually int, as we will discuss below). For example, if we had used the condition (int)r < 10 in the above for statement, the loop would continue two more iterations, showing 8 and 9 in the last two MessageBoxes.
An enumeration is defined using an enum statement, which is similar to a class statement except that in the simplest case, the body of an enum is simply a listing of the members of the enumeration. For example, the DialogResult enumeration is defined as follows:
public enum DialogResult
{
None, OK, Cancel, Abort, Retry, Ignore, Yes, No
}
This definition defines DialogResult.None as having the value 0, DialogResult.OK as having the value 1, etc.
As mentioned above, each enumeration has underlying type. By default, this type is int, but an enum statement may specify another underlying type, as follows:
public enum Beatles : byte
{
John, Paul, George, Ringo
}
The above construct defines the underlying type for the enumeration Beatles to be byte; thus, a variable of type Beatles may be assigned any byte value. The following integer types may be used as underlying types for enumerations:
- byte (0 through 255)
- sbyte (-128 through 127)
- short (-32,768 through 32,767)
- ushort (0 through 65,535)
- int (-2,147,483,648 through 2,147,483,647)
- uint (0 through 4,294,967,295)
- long (-9,223,372,036,854,775,808 through 9,223,372,036,854,775,807)
- ulong (0 through 18,446,744,073,709,551,615)
It is also possible to define members of an enumeration so that they are not simply the values 0, 1, etc. For example, we might alter the Beatles enumeration as follows:
public enum Beatles : byte
{
John = 1, Paul, George = 5, Ringo
}
This defines the following values for the members:
- Beatles.John: 1
- Beatles.Paul: 2
- Beatles.George: 5
- Beatles.Ringo: 6
Thus, if a value is explicitly assigned to a member, that member takes
on that value; otherwise, that member takes on the next value greater
than the previous member listed, or 0 if that member is the first
listed. Note that using this technique, it is possible to define two
members with the same value, although this is usually undesirable. If
assigning values in this way would lead to a value outside the range of
the underlying type, a syntax error results (for example, if George
were assigned 255 in the above definition, thus causing Ringo to have a value outside the range of a byte).
One reason we might want to define explicit values for members of an
enumeration is if we want to use the members as flags. For example, one
of the
MessageBox.Show
methods takes as one of its parameters a
MessageBoxOptions,
which is an enumeration containing the following members:
- MessageBoxOptions.DefaultDesktopOnly
- MessageBoxOptions.RightAlign
- MessageBoxOptions.RtlReading
- MessageBoxOptions.ServiceNotification
The meaning of each of these members is unimportant for the purposes of
this discussion. The point is that the values of these members are
chosen in such a way that more than one of them can be combined into a
single value. The way this is done is to define each member as a
different power of 2. The binary representation of a power of 2 contains
exactly one bit with a value of 1. Thus, these values can be combined
using a logical OR operator, and the original values can be retrieved
using a logical AND operator.
For example, suppose the MessageBoxOptions enumeration is defined as
follows:
public enum MessageBoxOptions
{
DefaultDesktopOnly = 1,
RightAlign = 2,
RtlReading = 4,
ServiceNotification = 8
}
Note
The definition in .NET 6 uses different powers of 2, but
the priciple is the same.
Now suppose we want to create a
MessageBox that will be displayed on the default desktop with
right-aligned text. We can combine these options using the expression
MessageBoxOptions.DefaultDesktopOnly | MessageBoxOptions.RightAlign
This expression combines corresponding bits of the two operands using a
logical OR. Recall that the logical OR of two bits is 1 if at least one
of the two bits is 1. If both operands are 0, the result is 0. In this
example, the operands have a 1 in different bit locations. When we
combine them using logical OR, both of these bit positions will contain
a 1:
0000 0000 0000 0000 0000 0000 0000 0001
0000 0000 0000 0000 0000 0000 0000 0010
---------------------------------------
0000 0000 0000 0000 0000 0000 0000 0011
We can therefore specify both of these options to the Show method as
folows:
MessageBox.Show("Hello\nworld!", "Hello", MessageBoxButtons.OK,
MessageBoxIcon.Information, MessageBoxDefaultButton.Button1,
MessageBoxOptions.DefaultDesktopOnly |
MessageBoxOptions.RightAlign);
The \n in the above example specifies the end of a line; hence,
“Hello” and “world!” will be displayed on separate lines, aligned on
the right:

The Show method determines which bits are 1 in the
MessageBoxOptions parameter using a logical AND. Recall that a
logical AND of two bits is 1 only if both bits are 1. In all othercases,
the result is 0. Suppose, then, that options is a
MessageBoxOptions variable with an unknown value. Because each named
member of the MessageBoxOptions enumeration (e.g.,
MessageBoxOptions.RightAlign) has exactly one bit with a value of 1,
an expression like
options & MessageBoxOptions.RightAlign
can have only two possible values:
- If the bit position containing the 1 in
MessageBoxOptions.RightAlign also contains a 1 in
options,
then the expression’s value is MessageBoxOptions.RightAlign. - Otherwise, the expression’s value is 0.
Thus, the Show method can use code like:
if ((options & MessageBoxOptions.RightAlign) == MessageBoxOptions.RightAlign)
{
// Code to right-align the text
}
else
{
// Code to left-align the text
}
Defining enumerations to be used as flags in this way can be made easier
by writing the powers of 2 in hexadecimal, or base 16. Each hex digit
contains one of 16 possible values: the ten digits 0-9 or the six
letters a-f (in either lower or upper case). A hex digit is exactly four
bits; hence, the hex values containing one occurrence of either 1, 2, 4,
or 8, with all other digits 0, are exactly the powers of 2. To write a
number in hex in a C# program, start with 0x, then give the hex
digits. For example, we can define the following enumeration to
represent the positions a baseball player is capable of playing:
public enum Positions
{
Pitcher = 0x1,
Catcher = 0x2,
FirstBase = 0x4,
SecondBase = 0x8,
ThirdBase = 0x10,
Shortstop = 0x20,
LeftField = 0x40,
CenterField = 0x80,
RightField = 0x100
}
We can then encode that a player is capable of playing 1st base, left
field, center field, or right field with the expression:
Positions.FirstBase | Positions.LeftField | Positions.CenterField | Positions.RightField
This expression would give a value having four bit positions containing
1:
0000 0000 0000 0000 0000 0001 1100 0100
For more information on enumerations, see the section,
Enumeration Types in the
C# Reference.
Structures
Structures
A structure is similar to a class, except that it is a value type, whereas a class is a reference type. A structure definition looks a lot like a class definition; for example, the following defines a structure for storing information associated with a name:
/// <summary>
/// Stores a frequency and a rank.
/// </summary>
public readonly struct FrequencyAndRank
{
/// <summary>
/// Gets the Frequency.
/// </summary>
public float Frequency { get; }
/// <summary>
/// Gets the Rank.
/// </summary>
public int Rank { get; }
/// <summary>
/// Initializes a FrequencyAndRank with the given values.
/// </summary>
/// <param name="freq">The frequency.</param>
/// <param name="rank">The rank.</param>
public FrequencyAndRank(float freq, int rank)
{
Frequency = freq;
Rank = rank;
}
/// <summary>
/// Obtains a string representation of the frequency and rank.
/// </summary>
/// <returns>The string representation.</returns>
public override string ToString()
{
return Frequency + ", " + Rank;
}
}
Note that the above definition looks just like a class definition, except that the keyword struct is used instead of the keyword class, and the readonly modifier is used. The readonly modifier cannot be used with a class definition, but is often used with a structure definition to indicate that the structure is immutable. The compiler then verifies that the structure definition does not allow any fields to be changed; for example, it verifies that no property has a set accessor.
A structure can be defined anywhere a class can be defined. However, one important restriction on a structure definition is that no field can be of the same type as the structure itself. For example, the following definition is not allowed:
public struct S
{
private S _nextS;
}
The reason for this restriction is that because a structure is a value type, each instance would need to contain enough space for another instance of the same type, and this instance would need enough space for another instance, and so on forever. This type of circular definition is prohibited even if it is indirect; for example, the following is also illegal:
public struct S
{
public T NextT { get; }
}
public struct T
{
public S? NextS { get; }
}
Because the NextT property uses the default implementation, each instance of S contains a hidden field of type T. Because T is a value type, each instance of S needs enough space to store an instance of T. Likewise, because the NextS property uses the default implementation, each instance of T contains a hidden field of type S?. Because S is a value type, each instance of T - and hence each instance of S - needs enough space to store an instance of S?, which in turn needs enough space to store an instance of S. Again, this results in circularity that is impossible to satisfy.
Any structure must have a constructor that takes no parameters. If one is not explicitly provided, a default constructor containing no statements is included. If one is explicitly provided, it must be public. Thus, an instance of a structure can always be constructed using a no-parameter constructor. If no code for such a constructor is provided, each field that does not contain an initializer is set to its default value.
If a variable of a structure type is assigned its default value, each of its fields is set to its default value, regardless of any initializers in the structure definition. For example, if FrequencyAndRank is defined as above, then the following statement will set both x.Frequency and x.Rank to 0:
FrequencyAndRank x = default;
Warning
Because the default value of a type can always be assigned to a variable of that type, care should be taken when including fields of reference types within a structure definition. Because the default instance of this structure will contain null values for all fields of reference types, these fields should be defined to be nullable. The compiler provides no warnings about this.
For more information on structures, see the section, “Structure types” in the C# Language Reference.
The decimal Type
The decimal Type
A
decimal
is a structure representing
a floating-point decimal number. The main difference between a
decimal and a float or a double is that a decimal can
store any value that can be written using no more than 28 decimal
digits, a decimal point, and optionally a ‘-’, without rounding. For
example, the value 0.1 cannot be stored exactly in either a float or
a double because its binary representation is infinite
(0.000110011…); however, it can be stored exactly in a decimal.
Various types, such as int, double, or string, may be
converted to a decimal using a Convert.ToDecimal method; for
example, if i is an int, we can convert it to a decimal with:
decimal d = Convert.ToDecimal(i);
A decimal is represented internally with the following three components:
- A 96-bit value v storing the digits
(0 ≤ v ≤ 79,228,162,514,264,337,593,543,950,335).
- A sign bit s, where 1 denotes a negative value.
- A scale factor d to indicate where the decimal point is
(0 ≤ d ≤ 28).
The value represented is then (-1)sv/10d.
For example, 123.456 can be represented by setting v to 123,456,
s to 0, and d to 3.
Read-Only and Constant Fields
Read-Only and Constant Fields
Field declarations may contain one of the the keywords readonly or const to indicate that these fields will always contain the same values. Such declarations are useful for defining a value that is to be used throughout a class or structure definition, or throughout an entire program. For example, we might define:
public class ConstantsExample
{
public readonly int VerticalPadding = 12;
private const string _humanPlayer = "X";
. . .
}
Subsequently throughout the above class, the identifier _humanPlayer will refer to the string, “X”. Because VerticalPadding is public, the VerticalPadding field of any instance of this ConstantsExample will contain the value 12 throughout the program. Such definitions are useful for various reasons, but perhaps the most important is that they make the program more maintainable. For example, VerticalPadding may represent some distance within a graphical layout. At some point in the lifetime of the software, it may be decided that this distance should be changed to 10 in order to give a more compact layout. Because we are using a readonly field rather than a literal 12 everywhere this distance is needed, we can make this change by simply changing the 12 in the above definition to 10.
When defining a const field, an initializer is required. The value assigned by the initializer must be a value that can be computed at compile time. For this reason, a constant field of a reference type can only be a string or null. The assigned value may be an expression, and this expression may contain other const fields, provided these definitions don’t mutually depend on each other. Thus, for example, we could add the following to the above definition:
private const string _paddedHumanPlayer = " " + _humanPlayer + " ";
const fields may not be declared as static, as they are already implicitly static.
A readonly field differs from a const field mainly in that it is initialized at runtime, whereas a const field is initialized at compile time. This difference has several ramifications. First, a readonly field may be initialized in a constructor as an alternative to using an initializer. Second, a readonly field may be either static or non-static. These differences imply that in different instances of the same class or structure, a readonly field may have different values.
One final difference between a readonly field and a const field is that a readonly field may be of any type and contain any value. Care must be taken, however, when defining a readonly reference type. For example, suppose we define the following:
private readonly string[] _names = { "Peter", "Paul", "Mary" };
Defining _names to be readonly guarantees that this field will always refer to the same array after its containing instance is constructed. However, it does not guarantee that the three array locations will always contain the same values. For this reason, the use of readonly for public fields of mutable reference types is discouraged.
readonly is preferred over const for a public field whose value may change later in the software lifecycle. If the value of a public const field is changed by a code revision, any code using that field will need to be recompiled to incorporate that change.
Properties
Properties
A property is used syntactically like a field of a class or structure,
but provides greater flexibility in implementation. For example, the
string class contains a public property called
Length. This
property is accessed in code much as if it were a public int
field; i.e., if s is a string variable, we can access its
Length property with the expression s.Length,
which evaluates to an int. If Length were a public int field, we would access it in just the same way. However, it turns out that we cannot assign a value to this property, as we can to a public field; i.e., the statement,
is not allowed. The reason for this limitation is that properties can be defined to restrict whether they can be read from or written to. The Length property is defined so that it can be read from, but not written to. This flexibility is one of the two main differences between a field and a property. The other main difference has to do with maintainability and is therefore easier to understand once we see how to define a property.
Suppose we wish to provide full read/write access to a double value. Rather than defining a public double field, we can define a simple double property as follows:
public double X { get; set; }
This property then functions just like a public field - the get keyword allows code to read from the property, and the set keyword allows code to write to the property. A property definition requires at least one of these keywords, but one of them may be omitted to define a read-only property (if set is omitted) or a write-only property (if get is omitted). For example, the following defines X to be a read-only property:
Although this property is read-only, the constructor for the class or structure containing this definition is allowed to initialize it. Sometimes, however we want certain methods of the containing class or structure to be able to modify the property’s value without allowing user code to do so. To accomplish this, We can define X in this way:
public double X { get; private set; }
The above examples are the simplest ways to define properties. They all rely on the default implementation of the property. Unlike a field, the name of the property is not actually a variable; instead, there is a hidden variable that is automatically defined. The only way this hidden variable can be accessed is through the property.
Warning
Don’t define a private property using the default implementation. Use a private field instead.
The distinction between a property and its hidden variable may seem artificial at first. However, the real flexibility of a property is revealed by the fact that we can define our own implementation, rather than relying on the default implementation. For example, suppose a certain data structure stores a StringBuilder called _word, and we want to provide read-only access to its length. We can facilitate this by defining the following property:
public int WordLength
{
get => _word.Length;
}
In fact, we can abbreviate this definition as follows:
public int WordLength => _word.Length;
In this case, the get keyword is implied. In either case, the code to the right of the “=>” must be an expression whose type is the same as the property’s type. Note that when we provide such an expression, there is no longer a hidden variable, as we have provided explicit code indicating how the value of the property is to be computed.
We can also provide an explicit implementation for the set accessor. Suppose, for example, that we want to allow the user read/write access to the length of _word. In order to be able to provide write access, we must be able to acquire the value that the user wishes to assign to the length. C# provides a keyword value for this purpose - its type is the same as the type of the property, and it stores the value that user code assigns to the property. Hence, we can define the property as follows:
public int WordLength
{
get => _word.Length;
set => _word.Length = value;
}
It is this flexibility in defining the implementation of a property that makes public properties more maintainable than public fields. Returning to the example at the beginning of this section, suppose we had simply defined X as a public double field. As we pointed out above, such a field could be used by user code in the same way as the first definition of the property X. However, a field is part of the implementation of a class or structure. By making it public, we have exposed part of the implementation to user code. This means that if we later change this part of the implementation, we will potentially break user code that relies on it. If, instead, we were to use a property, we can then change the implementation by modifying the get and/or set accessors. As long as we don’t remove either accessor (or make it private), such a change is invisible to user code. Due to this maintainability, good programmers will never use public fields (unless they are constants); instead, they will use public properties.
In some cases, we need more than a single to expression to define a get or set accessor. For example, suppose a data structure stores an int[ ] _elements, and we wish to provide read-only access to this array. In order to ensure read-only access, we don’t want to give user code a reference to the array, as the code would then be able to modify its contents. We therefore wish to make a copy of the array, and return that array to the user code (though a better solution might be to define an indexer). We can accomplish this as follows:
public int[ ] Elements
{
get
{
int[] temp = new int[_elements.Length];
_elements.CopyTo(temp, 0);
return temp;
}
}
Thus, arbitrary code may be included within the get accessor, provided it returns a value of the appropriate type; however, it is good programming practice to avoid changing the fields of a class or structure within the get accessor of one of its properties. In a similar way, arbitrary code may be used to implement a set accessor. As we can see from this most general way of defining properties, they are really more like methods than fields.
Given how similar accessors are to methods, we might also wonder why we don’t just use methods instead of properties. In fact, we can do just that - properties don’t give any functional advantage over methods, and in fact, some object-oriented languages don’t have properties. The advantage is stylistic. Methods are meant to perform actions, whereas properties are meant to represent entities. Thus, we could define methods GetX and SetX to provide access to the private field _x; however, it is stylistically cleaner to define a property called X.
Indexers
Indexers
Recall that the System.Collections.Generic.Dictionary<TKey, TValue> class (see “The Dictionary<TKey, TValue> Class”) allows keys to be used as indices for the purpose of adding new keys and values, changing the value associated with a key, and retrieving the value associated with a key in the table. In this section, we will discuss how to implement this functionality.
An indexer in C# is defined using the following syntax:
public TValue this[TKey k]
{
get
{
// Code to retrieve the value with key k
}
set
{
// Code to associate the given value with key k
}
}
Note the resemblance of the above code to the definition of a property. The biggest differences are:
- In place of a property name, an indexer uses the keyword
this. - The keyword
this is followed by a nonempty parameter list enclosed in square brackets.
Thus, an indexer is like a property with parameters. The parameters are the indices themselves; i.e., if d is a Dictionary<TKey, TValue> and key is a TKey, d[key] invokes the indexer with parameter key. In general, either the get accessor or the set accessor may be omitted, but at least one of them must be included. As in a property definition, the set accessor can use the keyword value for the value being assigned - in this case, the value to be associated with the given key. The value keyword and the return type of the get accessor will both be of type TValue, the type given prior to the keyword this in the above code.
We want to implement the indexer to behave in the same way as the indexer for System.Collections.Generic.Dictionary<TKey, TValue>. Thus, the get accessor is similar to the TryGetValue method, as outlined in “A Simple Hash Table Implementation”, with a few important differences. First, the get accessor has no out parameter. Instead, it returns the value that TryGetValue assigns to its out parameter when the key is found. When the key is not found, because it can’t return a bool to indicate this, it instead throws a KeyNotFoundException.
Likewise, the set accessor is similar to the Add method, as outlined in “A Simple Hash Table Implementation”. However, whereas the Add method has a TValue parameter through which to pass the value to be associated with the given key, the set accessor gets this value from the value keyword. Furthermore, we don’t want the set accessor to throw an exception if the key is found. Instead, we want it to replace the Data of the cell containing this key with a new KeyValuePair containing the key with the new value.
The Keywords static and this
The Keywords static and this
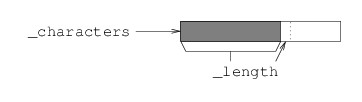
Object-oriented programming languages such as C# are centered on the concept of an object. Class and structure definitions give instructions for constructing individual objects of various types, normally by using the new keyword. When an object is constructed, it has its own fields in which values may be stored. Specifically, if type T has an int field called _length, then each object of type T will have have such a field, and each of these fields may store a different int. Thus, for example, if x and y are instances of type T, then x._length may contain 7, while y._length may contain 12.
Likewise, we can think of each object as having its own methods and properties, as when any of these methods or properties use the fields of the containing class or structure, they will access the fields belonging to a specific object. For example, if type T contains an Add method that changes the value stored in the _length filed, then a call x.Add will potentially change the value stored in x._length.
However, there are times when we want to define a field, method, or property, but we don’t want it associated with any specific object. For example, suppose we want to define a unique long value for each instance of some class C. We can define a private long field _id within this class and give it a value within its constructor. But how do we get this value in a way that ensures that it is unique? One way is to define a private static long field _nextId, as in the following code:
public class C
{
private static long _nextId = 0;
private long _id;
public C()
{
_id = _nextId;
_nextId++;
}
// Other members could also be defined.
}
By defining _nextId to be static, we are specifying that each instance of C will not contain a _nextId field, but instead, there is a single _nextId field belonging to the entire class. As a result, code belonging to any instance of C can access this one field. Thus, each time an instance of C is constructed, this one field is incremented. This field therefore acts as a counter that keeps track of how many instances of C have been constructed. On the other hand, because _id is not static, each instance of C contains an _id field. Thus, when the assignment,
is done, the value in the single _nextId field is copied to the value of the _id field belonging to the instance being constructed. Because the single _nextId field is incremented every time a new instance of C is constructed, each instance receives a different value for _id.
We can also define static methods or properties. For example, the MessageBox.Show(string text) method is static. Because it is static, we don’t need a MessageBox object in order to call this method - we simply call something like:
MessageBox.Show("Hello world!");
static methods can also be useful for avoiding NullReferenceExceptions. For example, there are times when we want to determine whether a variable x contains null, but x is of an unknown type (perhaps its type is defined by some type parameter T). In such a case, we cannot use == to make the comparison because == is not defined for all types. Furthermore, the following will never work:
Such code will compile, but if x is null, then calling its Equals method will throw a NullReferenceException. In all other cases, the if-condition will evaluate to false. Fortunately, a static Equals method is available to handle this situation:
Because this method is defined within the object class, which is a supertype of every other type in C#, we can refer to this method without specifying the containing class, just as if we had defined it in the class or structure we are writing. Because this method does not belong to individual objects, we don’t need any specific object available in order to call it. It therefore avoids a NullReferenceException.
Because a static method or property does not belong to any instance of its type, it cannot access any non-static members directly, as they all belong to specific instances of the type. If however, the code has access to a specific instance of the type (for example, this instance might be passed as a parameter), the code may reference non-static members of that instance. For example, suppose we were to add to the class C above a method such as:
public static int DoSomething(C x)
{
}
Code inside this method would be able to access _nextID, but not _id. Furthermore, it would be able to access any static methods or properties contained in the class definition, as well as all constructors, but no non-static methods or properties. However, it may access x._id, as well as any other members of x.
Code within a constructor or a non-static method or property can also access the object that contains it by using the keyword this. Thus, in the constructor code above, we could have written the line
as
In fact, the way we originally wrote the code is simply an abbreviation of the above line. Another way of thinking of the restrictions on code within a static method or property is that this code cannot use this, either explicitly or implicitly.
out and ref Parameters
out and ref Parameters
Normally, when a method is called, the call-by-value mechanism is used. Suppose, for example, we have a method:
private void DoSomething(int k)
{
}
We can call this method with a statement like:
provided n is an initialized variable consistent with the int type. For example, suppose n is an int variable containing a value of 28. The call-by-value mechanism works by copying the value of n (i.e., 28) to k. Whatever the DoSomething method may do to k has no effect on n — they are different variables. The same can be said if we had instead passed a variable k — the k in the calling code is still a different variable from the k in the DoSomething method. Finally, if we call DoSomething with an expression like 9 + n, the mechanism is the same.
If a parameter is of a reference type, the same mechanism is used, but it is worth considering that case separately to see exactly what happens. Suppose, for example, that we have the following method:
private void DoSomethingElse(int[] a)
{
a[0] = 1;
a = new int[10];
a[1] = 2;
}
Further suppose that we call this method with
int[] b = new int[5];
DoSomethingElse(b);
The initialization of b above assigns to b a reference to an array containing five 0s. The call to DoSomethingElse copies the value of b to a. Note, however, that the value of b is a reference; hence, after this value is copied, a and b refer to the same five-element array. Therefore, when a[0] is assigned 1, b[0] also becomes 1. When a is assigned a new array, however, this does not affect b, as b is a different variable — b still refers to the same five-element array. Furthermore, when a[1] is assigned a value of 2, because a and b now refer to different arrays, the contents of b are unchanged. Thus, when DoSomethingElse completes, b will refer to a five-element array whose element at location 0 is 1, and whose other elements are 0.
While the call-by-value mechanism is used by default, another mechanism, known as the call-by-reference mechanism, can be specified. When call-by-reference is used, the parameter passed in the calling code must be a variable, not a property or expression. Instead of copying the value of this variable into the corresponding parameter within the method, this mechanism causes the variable within the method to be an alias for the variable being passed. In other words, the two variables are simply different names for the same underlying variable (consequently, the types of the two variables must be identical). Thus, whatever changes are made to the parameter within the method are reflected in the variable passed to the method in the calling code as well.
One case in which this mechanism is useful is when we would like to have a method return more than one value. Suppose, for example, that we would like to find both the maximum and minimum values in a given int[ ]. A return statement can return only one value. Although there are ways of packaging more than one value together in one object, a cleaner way is to use two parameters that use the call-by-reference mechanism. The method can then change the values of these variables to the maximum and minimum values, and these values would be available to the calling code.
Specifically, we can define the method using out parameters:
private void MinimumAndMaximum(int[] array, out int min, out int max)
{
min = array[0];
max = array[0];
for (int i = 1; i < array.Length; i++)
{
if (array[i] < min)
{
min = array[i];
}
if (array[i] > max)
{
max = array[i];
}
}
}
The out keyword in the first line above specifies the call-by-reference mechanism for min and max. We could then call this code as follows, assuming a is an int[ ] containing at least one element:
int minimum;
int maximum;
MinimumAndMaximum(a, out minimum, out maximum);
When this code completes, minimum will contain the minimum element in a and maximum will contain the maximum element in a.
Warning
When using out parameters, it is important that the keyword
out is placed prior to the variable name in both the method call
and the method definition. If you omit this keyword in one of these
places, then the parameter lists won’t match, and you’ll get a syntax
error to this effect.
Tip
As a shorthand, you can declare an out parameter in the parameter
list of the method call. Thus, the above example could be shortened
to the following single line of code:
MinimumAndMaximum(a, out int minimum, out int maximum);
Note that out parameters do not need to be initialized prior to the method call in which they are used. However, they need to be assigned a value within the method to which they are passed. Another way of using the call-by-reference mechanism places a slightly different requirement on where the variables need to be initialized. This other way is to use ref parameters. The only difference between ref parameters and out parameters is that ref parameters must be initialized prior to being passed to the method. Thus, we would typically use an out parameter when we expect the method to assign it its first value, but we would use a ref parameter when we expect the method to change a value that the variable already has (the method may, in fact, use this value prior to changing it).
For example, suppose we want to define a method to swap the contents of two int variables. We use ref parameters to accomplish this:
private void Swap(ref int i, ref int j)
{
int temp = i;
i = j;
j = temp;
}
We could then call this method as follows:
int m = 10;
int n = 12;
Swap(ref m, ref n);
After this code is executed, m will contain 12 and n will contain 10.
The foreach Statement
The foreach Statement
C# provides a foreach statement that is often useful for iterating through the elements of certain data structures. A foreach can be used when all of the following conditions hold:
- The data structure is a subtype of either IEnumerable or IEnumerable<T> for some type T.
- You do not need to know the locations in the data structure of the individual elements.
- You do not need to modify the data structure with this loop.
Warning
Many of the data structures provided to you in CIS 300, as well as
many that you are to write yourself for this class, are not subtypes
of either of the types mentioned in 1 above. Consequently, we cannot
use a foreach loop to iterate through any of these data
structures. However, most of the data structures provided in the .NET
Framework, as well as all arrays, are subtypes of one of these types.
For example, the string class is a subtype of both IEnumerable
and IEnumerable<Char>. To see that this is the case, look in
the documentation for the string
class. In
the “Implements” section, we see all of the
interfaces implemented by string.
Because string implements both of these interfaces, it is a
subtype of each. We can therefore iterate through the elements (i.e., the characters) of a string using a foreach statement, provided we don’t need to know the location of each character in the string (because a string is immutable, we can’t change its contents).
Suppose, for example, that we want to find out how many times the letter ‘i’ occurs in a string s. Because we don’t need to know the locations of these occurrences, we can iterate through the characters with a foreach loop, as follows:
int count = 0;
foreach (char c in s)
{
if (c == 'i')
{
count++;
}
}
The foreach statement requires three pieces of information:
- The type of the elements in the data structure (char in the above example).
- The name of a new variable (
c in the above example). The type of this variable will be the type of the elements in the data structure (i.e., char in the above example). It will take on the values of the elements as the loop iterates. - Following the keyword in, the data structure being traversed (
s in the above example).
The loop then iterates once for each element in the data structure (unless a statement like return or break causes it to terminate prematurely). On each iteration, the variable defined in the foreach statement stores one of the elements in the data structure. Thus, in the above example, c takes the value of a different character in s on each iteration. Note, however, that we have no access to the location containing c on any particular iteration - this is why we don’t use a foreach loop when we need to know the locations of the elements. Because c takes on the value of each character in s, we are able to count how many of them equal ‘i’.
Occasionally, it may not be obvious what type to use for the
foreach loop variable. In such cases, if the data structure is a
subtype of IEnumerable<T>, then the type should be whatever type
is used for T. Otherwise, it is safe to use object. Note,
however, that if the data structure is not a subtype of
IEnumerable<T>, but you know that the elements are some specific
subtype of object, you can use that type for the loop variable -
the type will not be checked until the code is executed. For example,
ListBox
is a class that implements a GUI control displaying a list of
elements. The elements in the ListBox are accessed via its
Items
property, which gets a data structure of type
ListBox.ObjectCollection. Any
object can be added to this data structure, but we often just add strings. ListBox.ObjectCollection is a subtype of IEnumerable; however, it is permissible to set up a foreach loop as follows:
foreach (string s in uxList.Items)
{
}
where uxList is a ListBox variable. As long as all of the elements in uxList.Items are strings, no exception will be thrown.
While the foreach statement provides a clean way to iterate through a data structure, it is important to keep in mind its limitations. First, it can’t even be used on data structures that aren’t subtypes of IEnumerable or IEnumerable<T>. Second, there are many cases, especially when iterating through arrays, where the processing we need to do on the elements depends on the locations of the elements. For example, consider the problem of determining whether two arrays contain the same elements in the same order. For each element of one array, we need to know if the element at the same location in the other array is the same. Because the locations are important, a foreach loop isn’t appropriate - we should use a for loop instead. Finally, a foreach should never be used to modify a data structure, as this causes unpredictable results.
Even when a foreach would work, it is not always the best choice. For example, in order to determine whether a data structure contains a given element, we could iterate through the structure with a foreach loop and compare each element to the given element. While this would work, most data structures provide methods for determining whether they contain a given element. These methods are often far more efficient than using a foreach loop.
Enumerators
Enumerators
As we saw in the previous section, in order for a data structure to support a foreach loop, it must be a subtype of either IEnumerable or IEnumerable<T>, where T is the type of the elements in the data structure. Thus, because Dictionary<TKey, TValue> is a subtype of IEnumerable<KeyValuePair<TKey, TValue>>, we can use a foreach loop to iterate through the key-value pairs that it stores. Likewise, because its Keys and Values properties get objects that are subtypes of IEnumerable<TKey> and IEnumerable<TValue>, respectively, foreach loops may be used to iterate through these objects as well, in order to process all the keys or all the values stored in the dictionary. IEnumerable and IEnumerable<T> are interfaces; hence, we must define any subtypes so that they implement these interfaces. In this section, we will show how to implement the IEnumerable<T> interface to support a foreach loop.
The IEnumerable<T> interface requires two methods:
- public IEnumerator<T> GetEnumerator()
- IEnumerator IEnumerable.GetEnumerator()
The latter method is required only because IEnumerable<T> is a subtype of IEnumerable, and that interface requires a GetEnumerator method that returns a non-generic IEnumerator. Both of these methods should return the same object; hence, because IEnumerator<T> is also a subtype of IEnumerator, this method can simply call the first method:
IEnumerator IEnumerable.GetEnumerator()
{
return GetEnumerator();
}
The public GetEnumerator method returns an IEnumerator<T>. In order to get instances of this interface, we could define a class that implements it; however, C# provides a simpler way to define a subtype of this interface, or, when needed, the IEnumerable<T> interface.
Defining such an enumerator is as simple as writing code to iterate through the elements of the data structure. As each element is reached, it is enumerated via a yield return statement. For example, suppose a dictionary implementation uses a List<KeyValuePair<TKey, TValue>> called _elements to store its key-value pairs. We can then define its GetEnumerator method as follows:
public IEnumerator<KeyValuePair<TKey, TValue>> GetEnumerator()
{
foreach (KeyValuePair<TKey, TValue> p in _elements)
{
yield return p;
}
}
Suppose user code contains a Dictionary<string, int> called d and a foreach loop structured as follows:
foreach (KeyValuePair<string, int> x in d)
{
}
Then the GetEnumerator method is executed until the yield return is reached. The state of this method is then saved, and the value p is used as the value for x in the first iteration of the foreach in the user code. When this loop reaches its second iteration, the GetEnumerator method resumes its execution until it reaches the yield return a second time, and again, the current value of p is used as the value of x in the second iteration of the loop in user code. This continues until the GetEnumerator method finishes; at this point, the loop in user code terminates.
Before continuing, we should mention that there is a simpler way of implementing the public GetEnumerator method in the above example. Because List<T> implements IEnumerable<T>, we can simply use its enumerator:
public IEnumerator> GetEnumerator()
{
return _elements.GetEnumerator();
}
However, the first solution illustrates a more general technique that can be used when we don’t have the desired enumerator already available. For instance, continuing the above example, suppose we wish to define a Keys property to get an IEnumerable<TKey> that iterates through the keys in the dictionary. Because the dictionary now supports a foreach loop, we can define this code to iterate through the key-value pairs in the dictionary, rather than the key-value pairs stored in the List<KeyVauePair<TKey, TValue>>:
public IEnumerable<TKey> Keys
{
get
{
foreach (KeyValuePair<TKey, TValue> p in this)
{
yield return p.Key;
}
}
}
The above code is more maintainable than iterating through the List<KeyValuePair<TKey, TValue>> as it doesn’t depend on the specific implementation of the dictionary.
While this technique usually works best with iterative code, it can also be used with recursion, although the translation usually ends up being less direct and less efficient. Suppose, for example, our dictionary were implemented as in “Binary Search Trees”, where a binary search tree is used. The idea is to adapt the inorder traversal algorithm. However, we can’t use this directly to implement a recursive version of the GetEnumerator method because this method does not take any parameters; hence, we can’t apply it to arbitrary subtrees. Instead, we need a separate recursive method that takes a BinaryTreeNode<KeyValuePair<TKey, TValue>> as its parameter and returns the enumerator we need. Another problem, though, is that the recursive calls will no longer do the processing that needs to be done on the children - they will simply return enumerators. We therefore need to iterate through each of these enumerators to include their elements in the enumerator we are returning:
private static IEnumerable<KeyValuePair<TKey, TValue>>
GetEnumerable(BinaryTreeNode<KeyValuePair<TKey, TValue>>? t)
{
if (t != null)
{
foreach (KeyValuePair<TKey, TValue> p in GetEnumerable(t.LeftChild))
{
yield return p;
}
yield return t.Data;
foreach (KeyValuePair<TKey, TValue> p in GetEnumerable(t.RightChild))
{
yield return p;
}
}
}
Note that we’ve made the return type of this method IEnumerable<KeyValuePair<TKey, TValue>> because we need to use a foreach loop on the result of the recursive calls. Then because any instance of this type must have a GetEnumerator method, we can implement the GetEnumerator method for the dictionary as follows:
public IEnumerator<KeyValuePair<TKey, TValue>> GetEnumerator()
{
return GetEnumerable(_elements).GetEnumerator();
}
In transforming the inorder traversal into the above code, we have introduced some extra loops. These loops lead to less efficient code. Specifically, if the binary search tree is an AVL tree or other balanced binary tree, the time to iterate through this enumerator is in $ O(n \lg n) $, where $ n $ is the number of nodes in the tree. The inorder traversal, by contrast, runs in $ O(n) $ time. In order to achieve this running time with an enumerator, we need to translate the inorder traversal to iterative code using a stack. However, this code isn’t easy to understand:
public IEnumerator<KeyValuePair<TKey, TValue>> GetEnumerator()
{
Stack<BinaryTreeNode<KeyValuePair<TKey, TValue>>> s = new();
BinaryTreeNode<KeyValuePair<TKey, TValue>>? t = _elements;
while (t != null || s.Count > 0)
{
while (t != null)
{
s.Push(t);
t = t.LeftChild;
}
t = s.Pop();
yield return t.Data;
t = t.RightChild;
}
}
The switch Statement
The switch Statement
The switch statement provides an alternative to the if statement for certain contexts. It is used when different cases must be handled based on the value of an expression that can have only a few possible results.
For example, suppose we want to display a MessageBox containing “Abort”, “Retry”, and “Ignore” buttons. The user can respond in only three ways, and we need different code in each case. Assuming message and caption are strings, we can use the following code:
switch (MessageBox.Show(message, caption, MessageBoxButtons.AbortRetryIgnore))
{
case DialogResult.Abort:
// Code for the "Abort" button
break;
case DialogResult.Retry:
// Code for the "Retry" button
break;
case DialogResult.Ignore:
// Code for the "Ignore" button
break;
}
The expression to determine the case (in this example, the call to MessageBox.Show) is placed within the parentheses following the keyword switch. Because the value returned by this method is of the enumeration type DialogResult, it will be one of a small set of values; in fact, given the buttons placed on the MessageBox, this value must be one of three possibilities. These three possible results are listed in three case labels. Each of these case labels must begin with the keyword case, followed by a constant expression (i.e., one that can be fully evaluated by the compiler, as explained in the section, “Constant Fields”), followed by a colon (:). When the expression in the switch statement is evaluated, control jumps to the code following the case label containing the resulting value. For example, if the result of the call to MessageBox.Show is DialogResult.Retry, control jumps to the code following the second case label. If there is no case label containing the value of the expression, control jumps to the code following the switch statement. The code following each case label must be terminated by a statement like break or return, which causes control to jump elsewhere. (This arcane syntax is a holdover from C, except that C allows control to continue into the next case.) A break statement within a switch statement causes control to jump to the code following the switch statement.
The last case in a switch statement may optionally have the case label:
This case label is analogous to an else on an if statement in that if the value of the switch expression is not found, control will jump to the code following the default case label. While this case is not required in a switch statement, there are many instances when it is useful to include one, even if you can explicitly enumerate all of the cases you expect. For example, if each case ends by returning a value, but no default case is included, the compiler will detect that not all paths return a value, as any case that is not enumerated will cause control to jump past the entire switch statement. There are various ways of avoid this problem:
- Make the last case you are handling the default case.
- Add a default case that explicitly throws an exception to handle any cases that you don’t expect.
- Add either a return or a throw following the switch statement (the first two options are preferable to this one).
It is legal to have more than one case label on the same code block. For example, if i is an int variable, we can use the following code:
switch (i)
{
case 1:
// Code for i = 1
break;
case 2:
case 3:
case 5:
case 7:
// Code for i = 2, 3, 5, or 7
break;
case 4:
case 6:
case 8:
// Code for i = 4, 6, or 8
break;
default:
// Code for all other values of i
break;
}
If the value of the switch expression matches any one of the case labels on a block, control jumps to that block. The same case label may not appear more than once.
The Remainder Operator
The Remainder Operator
The remainder operator % computes the remainder that results when one number is divided by another. Specifically, suppose m and n are of some numeric type, where n ≠ 0. We can then define a quotient q and a remainder r as the unique values such that:
- qn + r = m;
- q is an integer;
- |qn| ≤ |m|; and
- |r| < |n|.
Then m % n gives r, and we can compute q by:
Another way to think about m % n is through the following algorithm to compute it:
- Compute |m| / |n|, and remove any fractional part.
- If m and n have the same sign, let q be the above result; otherwise, let q be the negative of the above result.
- m % n is m - qn.
Examples:
- 7 % 3 = 1
- -9 % 5 = -4
- 8 % -3 = 2
- -10 % -4 = -2
- 6.4 % 1.3 = 1.2
Subsections of Visual Studio
Installing Visual Studio
Installing Visual Studio
Visual Studio is available on the machines we use for CIS 300 labs, as well as on machines in other lab classrooms. This edition of Visual Studio is also freely available for installation on your own PC for your personal and classroom use. This section provides instructions for obtaining this software from Microsoft and installing it on your PC. The labs currently use Visual Studio 2022, though I encourage you to install the latest version available on your own machine (currently Visual Studio 2026).
Tip
Visual Studio can also be accessed via a remote desktop server. However, this server can only be accessed either from on-campus or through the campus VPN. See https://www.k-state.edu/it/cybersecurity/vpn// for details on the campus VPN. For more details on the remote desktop server, see the CS Department Support Wiki (this page can be accessed only from on-campus or through the campus VPN).
The enterprise edition of Visual Studio is also available through the Azure Dev Tools for Teaching program. See the CS Department Support Wiki (this page can be accessed only from on-campus or through the campus VPN) for details. A direct link to the Azure Dev Tools for Teaching portal is https://azureforeducation.microsoft.com/devtools.
While Microsoft also produces a version of Visual Studio for Mac, we recommend the Windows version. If you don’t have a Microsoft operating system, you can obtain one for free from the Azure Portal — see the CS Department Support Wiki (accessible only from on-campus or through the campus VPN) for details.
You will need to install the operating system either on a separate bootable partition or using an emulator such as VMware Fusion. VMware Fusion is also available for free through the VMware Academic Program — see the CS Department Support Wiki for details. To download Visual Studio, go to Microsoft’s Visual Studio Site, and click the “Download Visual Studio” button. This should normally begin downloading an installation file; if not, click the “click here to retry” link near the top of the page. When the download has completed, run the file you downloaded. This will start the installation process.
As the installation is beginning, you will be shown a window asking for the components to be installed. Click the “Workloads” tab in this window, and select “.NET desktop development” (under “Desktop & Mobile”). You can select other workloads or components if you wish, but this workload will install all you need for CIS 300.
The first time you run Visual Studio, you will be asked to sign in to your Microsoft account. You can either do this or skip it by clicking, “Not now, maybe later.” You will then be shown a window resembling the following:

Next to “Development Settings:”, select “Visual C#”. You can select whichever color scheme you prefer. At this point, Visual Studio should be fully installed and ready to use.
Git Repositories
Git Repositories
In CIS 300, start code for each assignment will be distributed via a Git repository. Git is a source control system integrated into Visual Studio 2022. Source control systems are powerful mechanisms for teams of programmers and other collaborators to manage multiple copies of various source files and other documents that all collaborators may be modifying. While CIS 300 does not involve teamwork, source control provides a convenient mechanism for distribution of code and submission of assignment solutions. In addition, as we will discuss later, source control provides mechanisms for accessing your code on multiple machines and for “checkpointing” your code.
At the heart of Git is the concept of a Git repository. A Git
repository is essentially a folder on your local machine. As you make
changes within this folder, Git tracks these changes. From time to
time, you will commit these changes. If you see that you have gone
down a wrong path, you can revert to an earlier commit. Git
repositories may be hosted on a server such as GitHub. Various users
may have copies of a Git repository on their own local machines. Git
provides tools for synchronizing local repositories with the
repository hosted on the server in a consistent way.
Note
The above description is a bit of an oversimplification, as the folder
comprising a local copy of a repository typically contains some files
and/or folders that are not part of the repository. One example of
such “extra” files might be
executables that are generated whenever source code within the
repository is compiled. However, when Visual Studio is managing a Git
repository, it does a good job of including within the repository any
files the user
places within the folder comprising the repository.
For each lab and homework assignment in CIS 300, you will be provided a URL that will create your own private Git repository on GitHub. The only people who will have access to your GitHub repositories are you, the CIS 300 instructors, and the CIS 300 lab assistants. These repositories will initially contain start code and perhaps data files for the respective assignments. You will copy the repository to your local machine by cloning it. When you are finished with the assignment, you will push the repository back to GitHub and submit its URL for grading. In what follows, we will explain how to create and clone a GitHub repository. Later in this chapter, we will explain how to commit changes, push a repository, and use some of the other features of Git.
Before you can access GitHub, you will need a GitHub account. If you don’t already have one, you can sign up for one at github.com. At some point after you have completed the sign-up process, GitHub will send you an email asking you to verify the email address you provided during the sign-up process. After you have done this, you will be able to set up GitHub repositories.
For each assignment in CIS 300, you will be given an invitation URL, such as:
Over the next few sections, we will be working through a simple example based on the above invitation link. If you wish to work through this example, click on the above link. You may be asked to sign in to GitHub, but once you are signed in, you will be shown a page asking you to accept the assignment. Clicking the “Accept this assignment” button will create a GitHub repository for you. You will be given a link that will take you to that repository. From that page you will be able to view all of the files in the repository.
In order to be able to use this repository, you will need to clone it
to your local machine. To do this, first open Visual Studio 2022, and
click on the “Clone a Repository” button on the right. In your web
browser, navigate to the GitHub repository that you wish to clone, and
click on the “Code” button. This will display a URL - click on the
button to its right to copy this URL to your clipboard. Then go back
to Visual Studio and paste this URL into the text
box labeled, “Repository location”. In the text box below that, fill
in a new folder you want to use for this repository on your machine,
then click the “Clone” button (if you are asked to sign in to GitHub, click the link to sign in through your web browser). This will copy the Git repository from
GitHub into the folder you selected, and open the solution it contains.
The following sections give an overview of how to use Visual Studio to edit and debug an application, as well as how to use Git within Visual Studio to maintain the local Git repository and synchronize it with the GitHub repository.
Visual Studio Solutions
Visual Studio Solutions
All code developed within Visual Studio 2022 must belong to one or more solutions. When you are using Visual Studio to develop a program, you will be working with a single solution. A solution will contain one or more projects. Each of these projects may belong to more than one solution. Each project typically contains several files, including source code files. Each file will typically belong to only one project. The following figure illustrates some of the possible relationships between solutions, projects, and files.
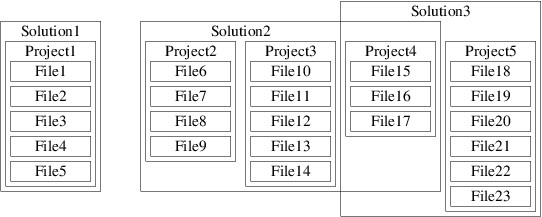

Note that in the above figure, Project4 is contained in both Solution2 and Solution3. In this section, we will focus on solutions that contain exactly one project, which in turn belongs to no other solutions (e.g., Solution1 in the above figure).
Whenever you open a solution in Studio 2022, the Solution Explorer
(which you can always find on the “View” menu) will give you a view of
the structure of your solution; for example, opening the solution in
the repository given in the previous section may result in the
following being shown in the Solution Explorer:

If you see the above, you will need to change to the Solution view, which you can get by double clicking the line that ends in “.sln”. This will give you the following view:

Warning
You ordinarily will not want to use Folder view, as this will cause files to be edited without any syntax or consistency checking. As a result, you can end up with a solution that is unusable. If your Solution Explorer ever looks like this:

(note the indication “Folder View” at the top and the absence of any boldface line), then it is in Folder view. To return to Solution view, click the icon indicated by the arrow in the above figure. This will return the Solution Explorer to the initial view shown above, where you can double-click the solution to select Solution view.
If you click on the small triangle to the left of
“Ksu.Cis300.HelloWorld”, you will get a more-detailed view:

Near the top, just under the search box, is the name of the solution with an indication of how many projects it contains. Listed under the name of the solution is each project, together with the various components of the project. One of the projects is always shown in bold face. The bold face indicates that this project is the startup project; i.e., it is the project that the debugger will attempt to execute whenever it is invoked (for more details, see the section, “The Debugger”).
The project components having a suffix of “.cs” are C# source code files. When a Windows Forms App is created, its project will contain the following three source code files:
Form1.cs: This file contains code that you will write in order to implement the main GUI for the application. It will be discussed in more detail in “The Code Window”.
Form1.Designer.cs: You will need to click the triangle to the
left of “Form1.cs” in the Solution Explorer in order to reveal this
file name. This contains automatically-generated code that completes
the definition of the main GUI. You will build this code indirectly
by laying out the graphical components of the GUI in the design window (see the section, “The Design Window” for more details). Ordinarily, you will not need to look at the contents of this file.
Program.cs: This file will contain something like the following:
namespace Ksu.Cis300.HelloWorld
{
internal static class Program
{
/// <summary>
/// The main entry point for the application.
/// </summary>
[STAThread]
static void Main()
{
// To customize application configuration such as set high DPI settings or default font,
// see https://aka.ms/applicationconfiguration.
ApplicationConfiguration.Initialize();
Application.Run(new Form1());
}
}
}
The Main method is where the application code begins. The last line of this method constructs a new instance of the class that implements the GUI. The call to Application.Run displays the GUI and starts a loop that processes events such as mouse clicks and keystrokes. Ordinarily, there is no need to look at this code.
One of the first things you will need to do when starting a new Windows Forms App is to change the name of Form1.cs, as this name (without the “.cs” suffix) is also the name of the class implementing the GUI. Therefore, it will need to be changed in order to conform to the naming convention for classes. To do this, right-click on its name in the Solution Explorer, and select “Rename” from the resulting popup menu. You will then be able to edit the name in the Solution Explorer - change it to “UserInterface.cs”. When you have entered the new name, the following window will be displayed:

You should click the “Yes” button in order to make the renaming consistent - particularly to rename the class as well.
The Design Window
The Design Window
The Design Window in Visual Studio is a window used to build graphical components. To open the Design Window for a graphical component, double-click on the component’s file name in the Solution Explorer. If you are working through the example from the previous two sections, double-click “UserInterface.cs” to open its Design Window. It will initially contain a blank form:

You can resize the form by dragging the handles on the right and
bottom edges. You can also change the title of the form (“Form1” in the picture above) as follows:
Click on the form.
If the Properties window isn’t showing on the right, select “Properties Window” from the “View” menu.
Look at the row of buttons near the top of the properties window,
and make sure the second and third buttons are highlighted:

If either of these buttons isn’t highlighted, click it to
highlight it. The first two buttons on this row toggle whether the
information is arranged by category (the first button) or
alphabetically (the second button). The next two buttons toggle
whether the control’s properties (the third button) or events (the
fourth button — we’ll discuss these below) are shown.
Find “Text” in the left column of the Properties window - it will
probably be highlighted. Click on the space to its right, and edit
the text to give your desired title. If you are working through
the example, give it a title of “Hello”.
For example, after resizing and changing the title, we might have a form that looks like this:

To add various graphical controls to the form, we use the Toolbox, which is normally available via a tab on the left edge (if not, you can always access it via the “View” menu). For example, let’s add a box that will contain text generated by the program. We open the Toolbox and click on the TextBox control, which can be found in the “Common Controls” section. We can then click on the design window (outside of the form) to bring it to the front, and drag an area on the form that we would like the TextBox to fill. After doing so, there will be a handle on the right and left edges to allow horizontal resizing (don’t worry about vertical resizing yet). You can also drag the TextBox to adjust its location. If you do this, as the edges of the TextBox approach the edges of the frame, struts will appear, helping you to leave an appropriate margin.
After adding a control, we usually need to customize it to some degree. To do this, click on it, then open the Properties window again. This window will now display the properties of the TextBox. The first property we will always want to change is the name of the variable that the program will use to refer to this control. This property is called “(Name)”, and will be near the top. You will need to change this name so that it follows the naming convention for controls on forms.
There are various properties that can be changed to customize the
appearance and behavior of a control. For example, we can change the
font of a TextBox by changing its Font property. This in turn
will affect the height of the TextBox. We can prevent the user
from editing it by setting its ReadOnly property to True. If
we want to allow multiple lines, we can set its Multiline property
to True. This in turn will add handles to the top and bottom edges
so that we can adjust its height. All of the properties of a GUI
control are documented in that control’s API documentation within the
.NET API browser.
Thus, continuing the above example, if we modify the TextBox’s variable name to uxDisplay, its Font property to Microsoft Sans Serif, 12pt and its ReadOnly property to True, we would have the following form:

Using a similar process, we can now add a Button to the form and name it uxGo. To change the text in the Button, we will need to change its Text property. This might give us the following:

Now that we have a Button on our form, it would be appropriate to provide some functionality for that Button. Clicking on a Button signals an event to which our program may respond. In order to cause our program to respond to such an event, we need to provide an event handler for it. Because a click is the default event for a Button, we can create an event handler for this event by simply double-clicking on the Button. Doing so will open a code window containing the contents of the source code file defining the current form. Furthermore, if the name of the Button is uxGo, the following method will have been added:
private void uxGo_Click(object sender, EventArgs e)
{
}
This method will be called whenever the Button is clicked (code causing this behavior will have been automatically added to the file containing the automatically-generated code for the form). Thus, to provide the appropriate functionality for the Button we just need to add code providing this functionality to this method. We will discuss this in more detail in the next section.
Before we leave the design window entirely, however, we need to talk about a more general way of accessing the event handlers associated with controls. Going back to the Properties window for a control, clicking the fourth button in the row of buttons near the top (the one that looks like a lightning bolt) will cause all of the possible events for that control to be displayed, and any event handler that has been created for that event. For example, if we have created the event handler described above, then the list of events for the Button looks like this:

This list is useful for two reasons. The more obvious reason is that we sometimes might want to handle an event that is not the default event for a control. For example, we might want a Button to react in some way (perhaps by changing color, for example) whenever the mouse enters or leaves it. In order to implement this functionality, we would need event handlers for the MouseEnter and MouseLeave events. We can add these event handlers by double-clicking these events in this list.
The less obvious use for this list is to remove an event handler. Often we find that we have added an event handler that we don’t need, perhaps by double-clicking in the wrong place. When this happens, shouldn’t just delete the code, because there is other automatically-generated code that refers to it. Deleting the code for an event handler would therefore lead to a syntax error. Instead, the proper way to remove an event handler is to go to the list of events, right-click on the name of the event, and select “Reset” from the resulting popup menu. This safely deletes the code and all automatically-generated references to it. (Sometimes it doesn’t delete the code, but if not, it is now safe to delete it.)
The Code Window
The Code Window
In the previous section, we designed the following GUI:

We also indicated briefly how functionality could be added to the button by double-clicking it in the design window to create an event handler. Creating this event handler also opens the code window to display it. The code window for this file can also be displayed by pressing F7 in the design window or by right-clicking the source code file name in the Solution Explorer and selecting “View Code”. Once a code window has been opened, it can be brought to the front by clicking the tab containing its file name near the top of the Visual Studio window. This window should look something like this:

Here is a ZIP archive containing the entire Visual Studio
solution. After downloading and expanding it, you may need to navigate through a folder or two, but you should be able to find a file, Ksu.Cis300.HelloWorld.sln (the “.sln” suffix may not be visible, but it should show as type “Microsoft Visual Studio Solution”). If you double-click on this file, Visual Studio 2022 should open the solution (if you have an older version of Visual Studio on your machine, you may need to right-click the file and select “Open with -> Microsoft Visual Studio 2022”).
Note in the class statement the keyword, partial. This indicates that not all of this class definition is in this file. The remainder of the definition is in the file, UserInterface.Design.cs. Recall that this file contains code for laying out the GUI and making the uxGo_Click method an event handler for the “Go” button. One of the method definitions that it contains is the InitializeComponent method, which does the layout of the GUI and sets up the event handlers. Recall also that the Main method in Program.cs constructs an instance of this class, then displays it and begins processing events for it. Because the constructor (see the code window above) calls the InitializeComponent method, everything will be set up to run the application - all that is needed is code for the event handler. This code will then be executed every time the “Go” button is clicked.
Before we add code to the event handler, let’s first take care of a couple of other issues. Note that in the code window shown above, lines 3 and 10 contain code underlined in green. These underlines indicate compiler warnings. While code containing warnings will execute, one of the requirements of CIS 300 is that all code submitted for grading be free of warnings (see Programming Style Requirements).
We can see each warning by hovering the mouse over the underlined code. For example, hovering over “UserInterface” in line 3 displays the following:

This warning refers to the CIS 300 style requirement that each class, structure, enumeration, field, property, and method be preceded by an appropriate comment (see Comments). To remove this warning, insert a new line prior to line 3, and type /// on this new line. This will cause an XML comment to be inserted:
/// <summary>
///
/// </summary>
public partial class UserInterface : Form
This is not quite enough to remove the warning. To accomplish this, text must be entered between <summary> and </summary>. Any non-blank text will remove the warning, but in order for the comment to be useful, the text should summarize the purpose of the class; for example,
/// <summary>
/// A GUI for a Hello World program.
/// </summary>
public partial class UserInterface : Form
Line 10 actually contains four warnings. Three of them can be removed by adding an appropriate comment, including descriptions of the two parameters (all event handlers in CIS 300 will have similar parameter lists, though the type of the second parameter will vary depending on the type of event that is being handled):
/// <summary>
/// Handles a Click event on the "Go" button.
/// </summary>
/// <param name="sender">The object signaling the event.</param>
/// <param name="e">Information about the event.</param>
private void uxGo_Click(object sender, EventArgs e)
These, comments, however, do not take care of the last warning, which states that uxGo_Click is not in Pascal case. This refers to the naming convention for methods. To fix this warning, we need to rename this event handler by removing ux and _.
Warning
Care must be taken when renaming an identifier, as all occurrences of the identifier need to be changed. In this case, some occurrences of this name are in the automatically-generated code in UserInterface.Designer.cs. Because the Design window relies on this code, failing to change these occurrences will cause the Design window to fail to open due to syntax errors in this file.
The safe way to change any identifier name within Visual Studio is to use its Rename feature. First, right-click on the name to be changed, and select “Rename…” from the resulting popup menu. This will open a dialog within which the name can be changed. Once the name is changed, press Enter to cause the identifier to be renamed globally.
All warnings should now be gone. However, the CIS 300 style requirements specify two other comments that need to be added (see Comments). First, an XML comment needs to be added to the constructor. Second, a comment containing the file name and the author’s name needs to be inserted at the top of the file, after inserting these comments, your code should resemble the following (with “Rod Howell” replaced by your name):
/* UserInterface.cs
* Author: Rod Howell
*/
namespace Ksu.Cis300.HelloWorld
{
/// <summary>
/// A GUI for a Hello World program.
/// </summary>
public partial class UserInterface : Form
{
/// <summary>
/// Constructs the GUI.
/// </summary>
public UserInterface()
{
InitializeComponent();
}
/// <summary>
/// Handles a Click event on the "Go" button.
/// </summary>
/// <param name="sender">The object signaling the event.</param>
/// <param name="e">Information about the event.</param>
private void GoClick(object sender, EventArgs e)
{
}
}
}
Now we can finally turn our attention to providing functionality to the “Go” button; i.e., we will add code to the GoClick event handler. In order for this code to provide meaningful functionality, it will need to interact with the controls on the GUI. It needs to use their variable names to do this. The name of the TextBox in this code is uxDisplay (recall that you can find this variable name by opening the design window, clicking on the control, and finding its “(Name)” property in its Properties window). Suppose we want to respond to the event by placing the text, “Hello world!”, in this TextBox. We therefore need to change its Text property to contain this string; i.e.:
private void GoClick(object sender, EventArgs e)
{
uxDisplay.Text = "Hello world!";
}
Notice that when you type a quote mark, a matching quote is automatically added following the text cursor. As long as you don’t reposition the text cursor, you can just type the closing quote as you normally would after typing the text string — Visual Studio won’t insert another quote mark, but will move the text cursor past the one it inserted automatically. The same behavior occurs when you type open parentheses, brackets, or braces.
The code window has several features that help with code writing. One of these features is auto-completion. Often while you are typing code, an auto-complete list appears, often with an entry highlighted. When an entry is highlighted (either automatically or by your selecting it manually), pressing “Enter” or typing a code element that can’t be part of the name (such as “.” or “+”) will insert the completion into your code. Once you get used to this feature, it can greatly speed up your code entry. Furthermore, it can be a helpful reminder of what you might need to type next. If you don’t want a name to auto-complete (perhaps because it is a name you haven’t defined yet), you can press “Esc”, and the auto-complete list will disappear.
Warning
If you are not using a lab machine, you might notice that as you type text, Visual Studio often provides auto-completions for the entire line. In some cases, the auto-completion is what you need, but in other cases, it is not. This feature can speed up the code-writing process for experienced programmers who use an auto-completion when they see that it matches what they were going to type. For inexperienced programmers, however, it can actually slow both the coding process and the learning process by making bad suggestions. If you find yourself using the auto-complete suggestions as hints, it would make sense to disable them, as these “hints” are often misleading. To disable this feature:
- From the “Tools” menu, select “Options…”.
- From the list on the left, select “IntelliCode”.
- In the large box in the upper-right, uncheck “Show whole line completions”.
- Save any changes, and restart Visual Studio.
This feature has been disabled on the lab machines.
Another feature of the code window is parameter information that shows as a popup box when you are typing a parameter list in a method call; for example:

This popup box gives the return type of the method, followed by the name of the method, followed by the parameter list, with the type of each parameter shown and the current parameter in bold face. When there are more than one method with the same name, this is indicated in the upper-left corner of the popup box (“1 of 21” in the figure above — the method shown is the first of 21 methods having that name). You can use either the arrows in the popup box or the up and down arrows on the keyboard to scroll through these different methods.
A related feature allows certain information to be obtained by hovering the mouse over different code elements. For example, hovering the mouse over an identifier will display the declaration and documentation for that identifier in a popup box. Also, hovering the mouse over a syntax error (indicated by a red underline, as shown under “Show” in the above figure) will display an explanation of the error, in addition to any information on the code element.
The Debugger
The Debugger
In previous sections, we discussed how a Windows Forms Application can be built using Visual Studio. Having built an application, we need to be able to run and test it. To do this, we use the Visual Studio Debugger. When an application is loaded into Visual Studio, we can invoke the debugger by clicking the “Start Debugging” button near the top:

When the debugger starts, it attempts to do the following things:
- Save any unsaved files.
- Compile the source code into executable code.
- Run the compiled code as an application.
If everything works correctly, the application is complete. Rarely, however, does everything work correctly the first time. Through the remainder of this section, we will discuss some of the ways the debugger can be used to find and fix errors.
One of the problems that can occur is that the compiler can fail to produce executable code because the source code contains syntax errors. When this happens, the following dialog is displayed:

Usually the best thing to do at this point is to click the “No” button. This will stop the debugger and display the error list. This error list can be displayed at any time by clicking the error list button at the bottom of the Visual Studio window:

Double-clicking on a syntax error within the error list will highlight the error in the code window. Normally, fixing the error will cause the corresponding entry in the error list to disappear; however, there are times when the entry won’t disappear until the debugger is started again (i.e., by clicking the “Start Debugging” button).
Once the syntax errors are removed, the debugger will be able to generate executable code and run it. However, more problems can occur at this point. One common problem is that an exception is thrown. For example, the GitHub repository created by this invitation link (see “Git Repositories”) contains a Visual Studio solution for a program to convert decimal numbers to base-16. Don’t worry about understanding the code, although the numerous comments may help you to do that. Instead, note that an exception is thrown when we try to convert 256:

This message gives us quite a bit of information already. First, it tells us which line threw the exception - the line highlighted in green. The arrow in the left margin tells us the same thing, but more generally, when the debugger is running, it indicates the line that is currently being executed or that is ready to be executed. The popup window indicates what kind of exception was thrown: an ArgumentOutOfRangeException. It also provides the additional information that a length was less than zero when it should not have been.
Having this information, we can now use the debugger to investigate further the cause of the exception. First, in order to see the code more clearly, we might want to close the popup window (we can always get it back by clicking the red circle containing the white ‘X’). We can now examine the values of any of the variables at the time the exception was thrown by hovering the mouse over them. For example, if we hover over lowOrder, a popup appears indicating that it has a value of “0”. If we move the mouse to hover over its Length property, we can see that it has a value of 1. Hovering over power shows that it has a value of 2. Thus, we can see that the exception was thrown because we gave the Substring method a length of 1 - 2 = -1. This can be confirmed by hovering the mouse over the “-” in the expression - the popup indicates that the value of the expression is, in fact, -1.
Actually fixing the error requires a little more understanding of the code. In this case, however, the comment immediately above the line in question helps us out. It tells us that the low-order part of the hex string we are building may need to be padded with 0s - this padding is what we are constructing. Furthermore, it tells us that the number of hex digits we need is the value of power. In order to get this many digits, we need to subtract the number of hex digits we already have in lowOrder from power; i.e., we need to reverse the order of the subtraction.
To stop the debugger, notice the buttons that are available at the top of the Visual Studio window while the debugger is running:

As you might guess, the “Stop” button stops the debugger. In what follows, we will discuss each of the other buttons indicated in the above figure, as well as other features of the debugger.
When debugging code, it is often useful to be able to pause execution at a particular place in order to be able to examine the values of variables as we did above. To accomplish this, we can set a breakpoint by clicking in the left margin of the code window at the line where we would like execution to pause. This places a large red dot in the margin where we clicked and colors the line red:

Whenever execution reaches a breakpoint, execution stops prior to executing that line. At this point, we can examine the values of variables as we described above. When we are ready to continue execution of the program, we click the “Continue” button. A breakpoint can be deleted by clicking on the red dot, or all breakpoints may be deleted by selecting “Delete All Breakpoints” from the “Debug” menu. A breakpoint may be disabled, but not deleted, by hovering over the large red dot and selecting “Disable” from the resulting popup. All breakpoints may be disabled by selecting “Disable All Breakpoints” from the “Debug” menu.
Sometimes we only want the execution to pause at a breakpoint when a certain condition is met. Such a situation might occur if we have a bug that only surfaces after the code containing it has already executed many times. Rather than letting the program stop and clicking “Continue” until we reach the point we are interested in, we can instead specify a condition on the breakpoint. To do this, right-click on the breakpoint in the left margin, and select “Conditions…” from the resulting popup menu. This causes a large box to be inserted into to the code below this line:
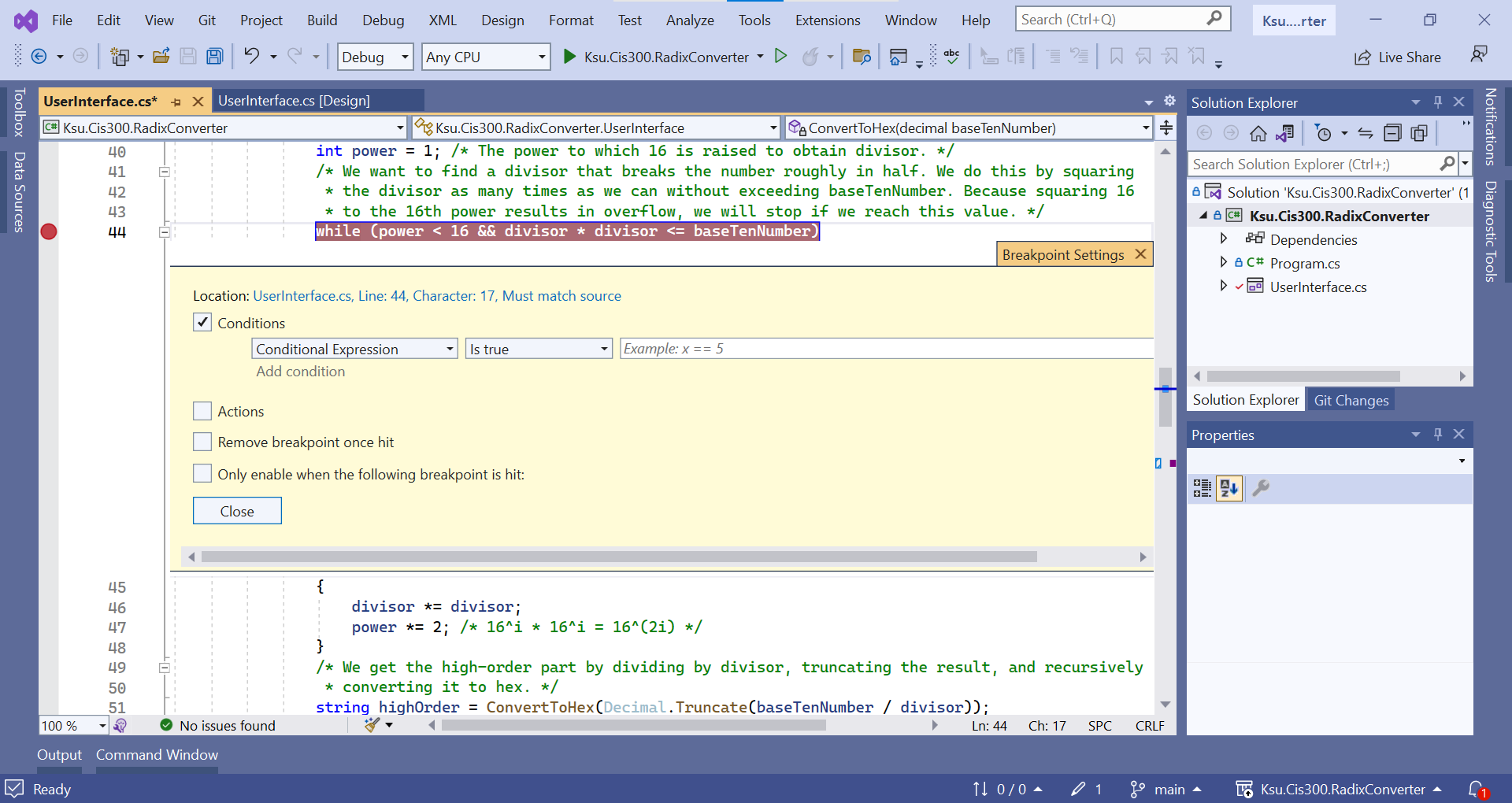

In this box, we can type an expression using variables visible at that program location. We can also choose whether we want execution to pause when that expression is true or whenever that expression has changed.
For example, we could add to the above breakpoint the condition:
Then when we run the debugger, execution will only pause at this breakpoint when power reaches a value of 8. Note that this line is executed at the top of each iteration of the loop; hence, the breakpoint condition is checked on each iteration.
While hovering the mouse over variable names is a useful way to
discover their current values, there are other mechanisms for doing
this as well. For example, while the debugger is paused, you can go to
the “Debug” menu and select “Windows -> Locals”. This will open a window displaying all of the local variables for the current method, property, or constructor, together with their current values. If the debugger is paused within a constructor or a non-static method or property, this window also contains this, which refers to the object that contains the constructor, method, or property. From this, you can access the non-static fields of this object.
Another mechanism for examining values of variables is through the “Immediate” window, which can also be accessed from the “Debug” menu via its “Windows” sub-menu. Within the Immediate window, you may type an expression involving the variables that are currently visible, press “Enter”, and it will display the value of that expression. This can be particularly useful when you have a large data structure, and you need to know a particular element in that structure. For example, suppose array is a large int[ ], and suppose i is an int. Using the “Locals” window, it might be rather tedious to find the value of array[i]. Using the Immediate window, however, you can just type in
and it will display its value.
When debugging, it is often useful to be able to step through the
execution of a piece of code so that you can see exactly what it is
doing. Three buttons are available for this purpose: “Step Into”,
“Step Over”, and “Step Out”. Suppose we were to run the code in the
GitHub repository provided above with the (unconditional) breakpoint shown in the above picture, and suppose we were to enter the value, 12345. Execution will then pause at this breakpoint with divisor equal to 16 and power equal to 1. Clicking either the “Step Into” button or the “Step Over” button will cause the debugger to evaluate the loop condition and, because its value is true, advance to the “{” on the next line. We may continue to walk through the execution a step at a time using either of these buttons - as long as we are in this loop, they will have the same effect. If the Locals window is open, whenever a variable changes value, this value will be shown in red.
After one iteration, the loop will terminate, and execution will reach the line where highOrder is defined. At this point, the functionality of the “Step Into” and “Step Over” buttons becomes different because this line contains a method call. The “Step Over” button will cause execution to run normally through the method call, and pause again as soon as the method call returns (however, because this is a recursive call, if the breakpoint is still set, execution will pause when it reaches the breakpoint within the recursive call). Thus, we can see the net effect of this method call without having to walk through it a step at a time. On the other hand, we might want to step through it in order to see what it is doing. We can do this using the “Step Into” button. If at some point we want to finish executing the method we are in, but pause after it returns, we can click the “Step Out” button.
When stepping through code, a “Watch” window is often a convenient way
to keep track of the value of one or more specific variables and/or
expressions. You can open a Watch window from the “Debug” menu under
“Windows -> Watch” — the four choices here are four different Watch windows that you may use (perhaps for debugging different parts of your program). A Watch window combines some of the advantages of the Locals window and the Immediate window. If you type in a value or expression, it will appear in the “Name” column, and if it can be evaluated in the current context, its value will be displayed in the “Value” column. Furthermore the value will be updated as the debugger executes code. You may list several values or expressions in the same Watch window, and their values will all be tracked. To delete an entry from a Watch window, right-click on it and select “Delete Watch”.
Submitting Assignments
Submitting Assignments
To submit a lab or homework assignment in CIS 300, you will need to do the following steps:
Commit your changes to your local Git repository. You will do this through the “Git Changes” tab in Visual Studio (if you don’t see this tab, click the icon that looks like a pencil at the bottom of the
Visual Studio window). In the “Git Changes” tab, in the box that says “Enter a message <Required>”, type in a message to be
associated with the changes you are committing.
Warning
Do not check the “Amend” box. This causes the previous commit to be changed, rather than creating a new commit. If this commit is already on GitHub, you will be unable to push your amended commit.
Push your committed changes to GitHub. Do this by clicking the
up-arrow icon at the top of the “Git Changes” tab. Note that only committed changes will be pushed. A message at the top of the “Git Changes” tab will indicate whether the push was successful.
Submit the URL of the commit you want graded using the submission
form provided in the assignment instructions. This requires the
following steps:
- Reload the GitHub repository for this assignment in your web
browser, and click on the link showing the number of commits
(this is in the top right corner of the list of files and
folders in the repository). This
will show a list of commits, beginning with the latest. To the
right of each commit is a button labeled “<>”. This button
links to a web page displaying the entire contents of that
commit. (It’s a good idea to check to see that all of your
source code files are present, in case something went wrong.)
The URL of this page will end in a 40-digit hexadecimal number
giving a digital fingerprint of the commit. Copy this entire URL to
the submission form at the bottom of the assignment.
- To complete your submission, click the “Submit Assignment”
button in the assignment submission form. The time at which
this button was clicked will be the official submission time
for your assignment.
Warning
It is important to do all three of these steps in this order. In
particular, if you make any changes between your last commit and the
push, these changes won’t be included in the submission. It is also important to include the correct URL.
Tip
You can double-check that all changes have been pushed by looking at
the numbers next to the up-down-arrows and pencil icons at the bottom of the
Visual Studio window. If all changes have been pushed, all numbers
should be 0.
Occasionally, problems can occur with the interface between Visual
Studio and GitHub. These problems can prevent your code from being
pushed to GitHub. While the problems can often be fixed, it is often
easier to bypass Visual Studio altogether, and use GitHub’s file
upload mechanism.
Warning
This is not the preferred assignment submission procedure because it
is less automated (and hence more error-prone), and it creates a
commit on GitHub that is not in your local git repository. However, it
can be used if the above procedure doesn’t work for you.
To use this alternative submission procedure, do the following steps:
If Visual Studio is running, exit this application, making sure all files are saved.
In your web browser, navigate to the repository for the assignment you are submitting. You should see a list of files and folders, including a file whose name ends with “.sln”.
In your Windows file browser, navigate to your project folder for this assignment. You should see the same list of files and folders as is shown in your web browser. (Depending on the settings for your local machine, you may not see file name suffixes such as “.sln” and “.gitignore”, and if you’ve added any projects that were not in the original repository, their folders may be shown in the file browser but not in the web browser.)
In your web browser, click the “Add file” button in the row of
buttons above the list of files and folders, and select
“Upload files” from the drop-down menu.
In your file browser, type Control-“A” to select all files and folders, and drag them to the web browser where it says, “Drag files here …”. The web browser should indicate a number of files being uploaded.
Near the bottom of the web browser window, in the text box below “Commit changes”, type a commit message, then click the “Commit changes” at the bottom. It may take a little while to process, but eventually you should see the repository again.
Make sure all of your “.cs” files are present in the GitHub repository, and that they contain the code you want. (If you have removed or renamed any files, the original files may still be in the repository; however, they shouldn’t be in the solution, and therefore shouldn’t interfere with the program’s execution.)
Submit the URL of this commit by following Step 3 of the assignment submission process given above.
Unit Testing
Unit Testing
Some of the lab assignments in CIS 300 use a technique called unit testing for testing the correctness of your code. Unit testing is an automated technique for testing individual public methods and properties using a pre-defined set of test cases. We will be using an open-source unit-testing framework called NUnit.
An NUnit test suite is a separate project contained within the same solution as the project it is to test. The GitHub repositories for lab assignments that utilize unit testing will initially contain these projects, whose names will typically end with “.Tests”. You should not modify these test projects.
A test project will contain one or more classes having the attribute, [TestFixture]. These classes will contain the specific tests, each of which is a method with the attribute, [Test]. The name of the method will briefly describe the test, and a more detailed explanation will be provided in comments.
To run the tests, first go to the
“Test” menu and select “Test Explorer”. This will open the Test
Explorer, which should resemble the following:

Note
Depending on whether the test project has been successfully compiled, the tests in the large panel may or may not be shown.
Then click the “Run All Tests in View” button in the upper-left corner of the Test Explorer. The Test Explorer should then show the results of all the tests:

Note
To see all of the output, you will need to open all of the elements either by
clicking on the small triangles to the left of each element or by clicking the icon containing the ‘+’ symbol.
The above output shows that there were two tests in the test suite. The names of the tests are simply the names of the methods comprising the tests. The output further shows that one of the tests, LengthIsCorrect, failed, whereas the other test, FirstElementIs2, passed.
The goal, of course, is to get all the tests to pass. When a test
fails, you will first want to refer to the comments on the test method
in order to understand what it is testing. Then by clicking on the
failed test in the Test Explorer, you can see exactly what failed in
the test - this will appear in the panel on the right. In some cases,
an unexpected result will have been produced. In such cases, the
message will show what result was expected, and what it actually
was. In other cases, an exception will have been thrown. In such
cases, the exception will be displayed. A stack trace will also be
displayed, so that you can tell what line of code threw the
exception. Finally, you can run the debugger on the test itself by
right-clicking on the test and selecting “Debug”. This will allow you
to debug your code using the techniques describe in the section, “The
Debugger”.
Tip
You can dock the Team Explorer into the main Visual Studio window by
clicking on the small triangle in the far upper-right corner of the
window and selecting either “Dock” or “Dock as Tabbed Document”.
One potential error deserves special mention. Sometimes code will
throw an exception that cannot be caught by a try-catch block. By
far the most common of these exceptions is the
StackOverflowException. When this exception is thrown during unit
testing, the test explorer will simply show some or all of the tests
in gray letters. This indicates that these tests were not
completed. To see why the tests were not completed, you can open the
“Output” window from the “View” menu and change the drop-down menu at the top to
“Tests”. This will indicate what error stopped the tests; for example,
the following indicates that a StackOverflowException has
occurred:

Unfortunately, when this error occurs, it’s more difficult to determine which test caused the exception. You can run the debugger on each test individually to see if it throws a StackOverflowException. In many cases, however, it is easier to examine each recursive call to make sure the call is made on a smaller problem instance.
When you believe you have fixed any errors in your code, you will
usually want to run all the tests again, as fixing one error can
sometimes introduce another. However, there are times, such as when
some of the tests are slow, when you don’t want to run all the
tests. In such cases, you can select an appropriate alternative from
the “Run” drop-down at the top of the Test Explorer (i.e., from the
drop-down button with the single green triangle on it). A useful option from this menu is “Run Failed Tests”. Alternatively, you can select one or more tests from the Test Explorer (use Ctrl-Click to select multiple tests), then right-click and select “Run”.
Whenever you run fewer than all the tests, the tests that were not run
are dimmed in the Test Explorer to indicate that these results are not
up to date. Be sure you always finish by running all the tests to make sure they all pass on the same version of your code.
Each CIS 300 lab assignment that uses unit testing is set up to use GitHub’s auto-grading feature, so that whenever the assignment is pushed, the server will run the unit tests. The overall result of the tests is indicated by an icon on the line below the “<> Code” button on the repository’s web page (you may need to refresh the page to show the latest commit). A brown dot indicates that the tests have not yet completed (this usually take a couple of minutes). A green check mark indicates that all tests have passed. A red X indicates that at least one test has failed, or that the tests couldn’t be run.
Unit testing will not be done by the GitHub server on any homework assignments in CIS 300. Instead, the auto-grading feature is used for a different purpose - to record push times. Thus, each push will result in an indication that all tests have passed, even if the code doesn’t compile.
You may receive emails indicating the results of auto-grading. You can control this behavior as follows:
- On any GitHub page, click on the icon in the upper-right corner and select “Settings”.
- On the navigation pane on the left, click “Notifications”.
- Scroll down to the “System” section, and select your desired notification behavior under “Actions”.
Using Multiple Machines
Using Multiple Machines
Source control provides one way to access your code from multiple machines. Before you decide to do this, however, you should consider whether this is the best approach. For example, if you have a CS Account, you have a network file system (the U: drive on CS Windows systems) that you can use whenever you have internet access. From off campus, you need to tunnel into campus using a Virtual Private Network, or VPN (see the KSU Information Technology Services page on Virtual Private Networking for instructions). Once on campus, you can mount this file system as a network drive by following the instructions on the CS support page, “DiskUsage”.
As an alternative to the U: drive or some cloud service, you can use your GitHub repositories to store a master copy of each assignment, and clone local copies as needed on the different machines you use. Once you have code in a GitHub repository, you can clone that repository to a local machine as described in “Git Repositories”. When you are finished working on that machine, commit all changes and push them to GitHub. If at some later point you need to resume working on a machine whose Git repository is out of date, you can update it by clicking the down-arrow icon in the Visual Studio “Git Changes” tab.
If you are careful about pushing all changes to GitHub and updating each local copy whenever you begin working on it, everything should go smoothly. Problems can occur, however, if you have made changes to a local version that is out of date, then either try to update it by pulling the GitHub copy, or try to push these changes to GitHub. In such cases, the following message will be shown:

At this point, you should click the “Pull then Push” button in the above message. This usually won’t fix the problem, as indicated by an error message at the top of the “Git Changes” tab. In order to resolve the conflicts in the two versions, look in the “Unmerged Changes” section of the “Git Changes” tab. This will list the files that are different in the two versions. To resolve the conflicts in a file, right-click on it, and select “Merge…”. Visual Studio will then show the two versions of the file side by side with the conflicts highlighted. If you want the version you are currently trying to push, simply click the “Take Current” button at the top. Otherwise, you can select individual portions from the two versions - the result will be shown below the two versions. When you are satisfied with the result, click the “Accept Merge” button. Once you have merged all conflicting files, you will then need to commit and push again.
Checkpointing
Checkpointing
Sometimes when writing code, we see that we have gone down a wrong path and would like to undo some major changes we have made. Source control can help us with this if we checkpoint by committing our changes from time to time, using commit messages that clearly describe the changes made in that commit. (Note that it is not necessary to push these commits to GitHub until you are ready to submit the assignment.) Git’s revert feature allows us to undo any of these commits.
Before you access Git’s revert feature, you should undo any uncommitted changes. To do this, go to the “Git Changes” tab, right-click on the first line under “Changes”, and select “Undo Changes”. You will be asked to confirm this action. This will undo any changes to that folder. If you have more folders containing changes, repeat this process for each changed folder.
To access Git’s revert feature, select “View Branch History” from the “Git” menu. This will reveal a list of all the commits for this local Git repository, with the most recent commit listed at the top. To undo all of the changes in any commit, right-click on that commit, and select “Revert” from the popup menu. The result is automatically committed.
Warning
You should always revert commits starting with the most recent and working backwards (i.e., from the top of the list toward the bottom). Otherwise, you will probably encounter conflicts that need to be resolved, as described in the previous section. You may even reach a state in which no commits can be reverted.