Stacks and Queues :: Data Structures in C#

Stacks and Queues

Often in solving problems, we need to access data items in a particular order. Consider, for example, the action of an “Undo” operation in a text editor, spreadsheet, or similar application. If we want to be able to undo a sequence of these operations, we need to record each operation as it is done. When we want to undo an operation, we need to retrieve the operation to undo from the recorded sequence of operations. However, we don’t want to undo just any operation in this sequence - we need to undo the most recent one that hasn’t yet been undone. We therefore need to access the operations in last-in-first-out, or LIFO, order. Other applications might need to access data items in first-in-first-out, or FIFO, order. In this chapter, we will examine data structures that support these kinds of access.

Introduction to Stacks

A stack provides last-in-first-out (LIFO) access to data items. We usually think of a stack as arranging data items vertically, like a stack of trays in a cafeteria. Access is normally provided only at the top of the stack; hence, if we want to add an item, we push it onto the top, and if we want to remove an item, we pop it from the top. Because we only access the top of the stack, the item that we pop is always the remaining item that we had pushed the most recently.

.NET provides two kinds of stacks. One is the Stack class found in the System.Collections namespace. Because this namespace isn’t typically included in the list of namespaces searched by the compiler, but the namespace containing the other Stack definition (discussed a bit later below) is included, we need to refer to it in code as System.Collections.Stack. This class provides a stack of object?s. Because every type in C# is a subtype of object, we can push any data items we want onto a Stack. Because object? is a nullable type, we can even push null. The most commonly-used public members of this class are:

A constructor that takes no parameters and constructs an empty stack.
A Count property, which gets the number of elements on the Stack as an int.
A Push method, which takes a single parameter of type object?, and pushes it onto the top of the Stack.
A Peek method, which takes no parameters and returns the element at the top of the Stack (as an object?) without changing the Stack’s contents. If the Stack is empty, this method throws an InvalidOperationException.
A Pop method, which takes no parameters, and removes and returns the element at the top of the Stack (as an object?). If the Stack is empty, this method throws an InvalidOperationException.

As we mentioned above, because the Push method takes an object? as its parameter, we can push any data elements we want, including null, onto a Stack. What this means, however, is that the compiler can’t determine the type of these elements when we retrieve them; i.e., both the Peek and Pop methods return object?s. Thus, for example, the following code will not compile:

System.Collections.Stack s = new();
s.Push(7);
int n = s.Pop() + 1;

The problem is that the Pop method returns an object?, and we can’t add an int to an object?. Although it’s pretty easy to see from this code that Pop will return 7, in many cases it’s impossible to know at compile time the exact type of the element returned (for example, the Stack may be a parameter to a public method, and that method may be called by code that has not yet been written). Consequently, the compiler simply uses the return type of Pop - it doesn’t even try to figure out the type any more precisely.

If you want to use the value returned by Pop or Peek as something other than an object?, you need to tell the compiler what its type actually is. You do this with a cast:

int n = (int)s.Pop() + 1;

This tells the compiler to assume that the value returned by Pop is an int. The type is still checked, but now it is checked at run time, rather than at compile time. If the runtime environment detects that the value is not, in fact, an int, it will throw an InvalidCastException.

While the above line of code will now compile, it generates a warning because Pop might return null, which cannot be cast to int. In order to avoid this warning, once we have determined that the call won’t return a null value, we need to use the ! operator:

// The element on the top of the stack is the int 7
int n = (int)s.Pop()! + 1;

Note that we include a comment explaining why Pop won’t return null here.

Often when we need a stack, the data items that we wish to store are all of the same type. In such a case, it is rather awkward to include a cast whenever we retrieve an item from the stack. In order to avoid this casting, .NET provides a generic stack, Stack<T>, found in the System.Collections.Generic namespace. The T within angle brackets is a type parameter - we may replace it with any type we want. This type tells what type of elements may be placed in this stack. For example, if we want a stack that will only contain ints, we can write:

Stack<int> s = new();

This class has members similar to those listed above for the non-generic Stack class, except that the Push method takes a parameter of type T (i.e., whatever type we placed within the angle brackets in the type declaration and constructor call), and the Peek and Pop methods each return a value of type T. As a result, the following is now legal code:

Stack<int> s = new();
s.Push(7);
int n = s.Pop() + 1;

We will show how you can define your own generic types in “Implementing a Stack”. First, however, we want to work through two example applications of stacks. We will do that in the next two sections.

Implementing Undo and Redo for a TextBox

A TextBox has a rather crude Undo/Redo feature. By right-clicking on a TextBox, a popup menu containing an Undo entry is presented. This Undo will undo only one action, which may include several edits. An immediate subsequent Undo will undo the Undo - in essence, a Redo. The same behavior can be achieved using Ctrl+Z. A more powerful Undo/Redo feature would allow an arbitrary sequence of edits to be undone, with the option of redoing any of these Undo operations. This section outlines various ways of implementing such a feature.

We first observe that when we perform an Undo, we want to undo the most recent edit that has not been undone; i.e., we need LIFO access to the edits. Likewise, when we perform a Redo, we want to redo the most recent Undo that has not been redone. Again, we need LIFO access to the Undo operations. We will therefore use two stacks, one to keep the edit history, and one to keep the Undo history (i.e., the history of Undo operations that can be redone).

Before we can define these stacks, we need to determine what we will be storing in them; i.e., we need to determine how we will represent an edit. We will consider several ways of doing this, but the simplest way is to store the entire contents of the TextBox after each edit. Proceeding in this way, we really aren’t representing edits at all, but we certainly would have the information we need to undo the edits. Likewise, the Undo history would store the entire contents of the TextBox prior to each Undo. Because the contents of the TextBox form a string, we need two private fields, each referring to a stack of strings:

/// <summary>
/// The history of the contents of the TextBox.
/// </summary>
private Stack<string> _editingHistory = new();

/// <summary>
/// The history of TextBox contents that have been undone and can be redone.
/// </summary>
private Stack<string> _undoHistory = new();

Before we can proceed to implementing the Undo and Redo operations, we need to do a bit more initialization. Note that by the way we have defined _editingHistory, this stack needs to contain the initial contents of the TextBox. Therefore, assuming the TextBox field is named uxEditBuffer, we need to add the following line to the end of the constructor of our user interface:

_editingHistory.Push(uxEditBuffer.Text);

In order to support Undo and Redo, we need to be able to record the content of uxEditBuffer each time it is modified. We can do this via an event handler for the TextChanged event on the TextBox. Because this event is the default event for a TextBox, we can add such an event handler by double-clicking on the TextBox within the Visual Studio® Design window. This event handler will then be called every time the contents of the TextBox are changed.

We need to deal with one important issue before we can write the code for this event handler. Whenever we perform an Undo or Redo operation, we will change the contents of the TextBox. This will cause the TextChanged event handler to be called. However, we don’t want to treat an Undo or a Redo in the same way as an edit by the user. For example, if the user does an Undo, we don’t want that Undo to be considered an edit, or a subsequent Undo would just undo the Undo; i.e., it would perform a Redo rather than an Undo.

Fortunately, there is an easy way to distinguish between an edit made by the user and a change made by the program code. A TextBox has a Modified property, which is set to true when the user modifies the TextBox contents, and is set to false when the program modifies the contents. Thus, we only want to record the TextBox contents when this property is true. Assuming the TextBox is named uxEditBuffer, we can then set up the event handler as follows:

/// <summary>
/// Handles a TextChanged event on the edit buffer.
/// </summary>
/// <param name="sender">The object signaling the event.</param>
/// <param name="e">Information about the event.</param>
private void EditBufferTextChanged(object sender, EventArgs e)
{
    if (uxEditBuffer.Modified)
    {
        RecordEdit();
    }
}

Now let’s consider how to write the RecordEdit method. Suppose there are two GUI controls (e.g., menu items or buttons) called uxUndo and uxRedo, which invoke the Undo and Redo operations, respectively. These controls should be enabled only when there are operations to undo or redo. Thus, initially these controls will be disabled. Whenever the user modifies the contents of the TextBox, we need to do the following:

Push the resulting text onto _editingHistory.
Enable uxUndo, as there is now an edit that can be undone.
Clear the contents of _undoHistory, as the last change to the TextBox contents was not an Undo. (A Stack<T> has a Clear method for this purpose.)
Disable uxRedo.

We therefore have the following method:

/// <summary>
/// Records an edit made by the user.
/// </summary>
private void RecordEdit()
{
    _editingHistory.Push(uxEditBuffer.Text);
    uxUndo.Enabled = true;
    _undoHistory.Clear();
    uxRedo.Enabled = false;
}

Now that we have a mechanism for recording the user’s edits, we can implement the Undo operation. The contents of the TextBox following the last edit (i.e, the current contents of the TextBox) should always be at the top of _editingHistory. An Undo should change the current contents to the previous contents - i.e., to the next string on _editingHistory. However, we don’t want to lose the top string, as this is the string that would need to be restored by a subsequent Redo. Instead, we need to push this string onto _undoHistory. We then need to enable uxRedo. In order to determine whether uxUndo should be enabled, we need to know how many elements remain in _editingHistory. We know there is at least one string on this stack - the string that we placed in the TextBox. There is an edit to undo if there is at least one more element on this stack - i.e., if its Count is greater than 1. We therefore have the following event handler for a Click event on uxUndo:

/// <summary>
/// Handles a Click event on Undo.
/// </summary>
/// <param name="sender">The object signaling the event.</param>
/// <param name="e">Information about the event.</param>
private void UndoClick(object sender, EventArgs e)
{
    _undoHistory.Push(_editingHistory.Pop());
    uxRedo.Enabled = true;
    uxEditBuffer.Text = _editingHistory.Peek();
    uxUndo.Enabled = _editingHistory.Count > 1;
}

The implementation of Redo is similar, but now we need to transfer a string between the stacks in the opposite direction - we move the top string from _undoHistory to _editingHistory. Then uxRedo should be enabled if any more strings remain in _undoHistory. The string we removed from _undoHistory should be placed in the TextBox. Finally, uxUndo should be enabled. We therefore have the following event handler for a Click event on uxRedo:

/// <summary>
/// Handles a Click event on Redo.
/// </summary>
/// <param name="sender">The object signaling the event.</param>
/// <param name="e">Information about the event.</param>
private void RedoClick(object sender, EventArgs e)
{
    _editingHistory.Push(_undoHistory.Pop());
    uxRedo.Enabled = _undoHistory.Count > 0;
    uxEditBuffer.Text = _editingHistory.Peek();
    uxUndo.Enabled = true;
}

This solution will work, except that an Undo or Redo always brings the text caret to the beginning of the TextBox contents. Furthermore, if the TextBox contains a long string, each edit causes a long string to be placed onto _editingHistory. This can quickly eat up a lot of memory, and may eventually fill up all available storage. In what follows, we will outline two better approaches.

The idea for both of these approaches is that instead of recording the entire contents of the TextBox for each edit, we only record a description of each edit. A single edit will either be an insertion or a deletion of some text. The number of characters inserted/deleted may vary, as the edit may be a cut or a paste (if we select a block of text and do a paste, the TextChanged event handler is actually called twice - once for the deletion of the selected text, and once for the insertion of the pasted text). We can therefore describe the edit with the following three values:

A bool indicating whether the edit was an insertion or a deletion.
An int giving the index of the beginning of the edit.
The string inserted or deleted.

We can maintain this information in stacks in one of two ways. One way is to use non-generic stacks and to push three items onto a stack for each edit. If we do this, we need to realize that when we pop elements from the stack, they will come out in reverse order from the way they were pushed onto it. Alternatively, we can define a class or a structure to represent an edit using the three values above as private fields. We can then use generic stacks storing instances of this type.

Whichever way we choose to represent the edits, we need to be able to compute each of the three pieces of information describing the edit. In order to compute this information, we need to compare the current contents of the TextBox with its prior contents in order to see how it changed. This means that, in addition to the two private fields we defined for the stacks, we will also need a private field to store the last string we saw in the TextBox. Rather than initializing _editingHistory within the constructor, we should now initialize this string in its place (because there will have been no edits initially, both stacks should initially be empty). If we keep this string field up to date, we will always have a “before” picture (the contents of this field) and an “after” picture (the current contents of the TextBox) for the edit we need to record.

To determine whether the edit was an insertion or a deletion, we can compare the lengths of the current TextBox contents and its previous contents. If the current content is longer, then the edit was an insertion; otherwise, the edit was a deletion. We therefore have the following method for this purpose:

/// <summary>
/// Returns whether text was deleted from the given string in order to
/// obtain the contents of the given TextBox.
/// </summary>
/// <param name="editor">The TextBox containing the result of the edit.</param>
/// <param name="lastContent">The string representing the text prior
/// to the edit.</param> 
/// <returns>Whether the edit was a deletion.</returns>
private bool IsDeletion(TextBox editor, string lastContent)
{
    return editor.TextLength < lastContent.Length;
}

Note that the above code uses the TextBox’s TextLength property. This is more efficient than finding the length of its Text property because evaluating the Text property requires all the characters to be copied to a new string.

Before getting either the location of the edit or the edit string itself, it is useful to compute the length of the edit string. This length is simply the absolute value of the difference in the lengths of the string currently in the TextBox and the last string we saw there. The Math class (in the System namespace) contains a static method Abs, which computes the absolute value of an int. We therefore have the following method:

/// <summary>
/// Gets the length of the text inserted or deleted.
/// </summary>
/// <param name="editor">The TextBox containing the result of the edit.</param>
/// <param name="lastContent">The string representing the text prior
/// to the edit.</param> 
/// <returns>The length of the edit.</returns>
private int GetEditLength(TextBox editor, string lastContent)
{
    return Math.Abs(editor.TextLength - lastContent.Length);
}

Now that we can determine whether an edit is a deletion or an insertion, and we can find the length of the edit string, it isn’t hard to find the beginning of the edit. First, suppose the edit is a deletion. The point at which the deletion occurred is the point at which the text caret now resides. We can find this point using the TextBox’s SelectionStart property. When there is no current selection - and there never will be immediately following an edit - this property gives the location of the text caret in the TextBox. Now consider the case in which the edit was an insertion. When text is inserted into a TextBox, the text caret ends up at the end of the inserted text. We need to find its beginning. We can do this by subtracting the length of the edit string from the text caret position. We therefore have the following method:

/// <summary>
/// Gets the location of the beginning of the edit.
/// </summary>
/// <param name="editor">The TextBox containing the result of the edit.</param>
/// <param name="isDeletion">Indicates whether the edit was a deletion.</param>
/// <param name="len">The length of the edit string.</param>
/// <returns>The location of the beginning of the edit.</returns>
private int GetEditLocation(TextBox editor, bool isDeletion, int len)
{
    if (isDeletion)
    {
        return editor.SelectionStart;
    }
    else
    {
        return editor.SelectionStart - len;
    }
}

The last piece of information we need is the string that was deleted or inserted. If the edit was a deletion, this string can be found in the previous TextBox contents. Its beginning is the point at which the edit occurred. We can therefore extract the deleted string from the previous contents using its Substring method. We pass this method the beginning index of the substring and its length, and it returns the substring, which is the deleted string. On the other hand, if the edit was an insertion, we can find the inserted string in the current TextBox contents by using its Substring in a similar way. We therefore have the following method:

/// <summary>
/// Gets the edit string.
/// </summary>
/// <param name="content">The current content of the TextBox.</param>
/// <param name="lastContent">The string representing the text prior
/// to the edit.</param> 
/// <param name="isDeletion">Indicates whether the edit was a deletion.</param>
/// <param name="editLocation">The location of the beginning of the edit.</param>
/// <param name="len">The length of the edit.</param>
/// <returns>The edit string.</returns>
private string GetEditString(string content, string lastContent, bool isDeletion, int editLocation, int len)
{
    if (isDeletion)
    {
        return lastContent.Substring(editLocation, len);
    }
    else
    {
        return content.Substring(editLocation, len);
    }
}

Using the methods above, we can modify the RecordEdit method to obtain the three values listed above to describe an edit. Once we have placed these three values onto the stack of editing history, we also need to update the string giving the previous TextBox contents. This should now be the current TextBox contents. We can then finish the method as shown above.

In order to implement Undo and Redo, we need to be able to insert and delete text in the TextBox. A string has two methods we can use to accomplish this:

The Remove method takes as its parameters the beginning index and length of the portion to remove, and returns the result.
The Insert method takes as its parameters the index at which the string should be inserted, and the string to insert. It returns the result.

Given the location of the edit along with the edit string itself, we can easily provide the parameters to the appropriate method above. Furthermore, it is not hard to set the location of the text caret using the TextBox’s SelectionStart property - we just need to be sure to add the length of the edit string if we are inserting text. The following method therefore performs a given edit, updating the string containing the last contents of the TextBox as well (we assume this string is called _lastText):

/// <summary>
/// Performs the given edit on the contents of the given TextBox.
/// </summary>
/// <param name="editor">The TextBox to edit.</param>
/// <param name="isDeletion">Indicates whether the edit is a deletion.</param>
/// <param name="loc">The location of the beginning of the edit.</param>
/// <param name="text">The text to insert or delete.</param>
private void DoEdit(TextBox editor, bool isDeletion, int loc, string text)
{
    if (isDeletion)
    {
        _lastText = editor.Text.Remove(loc, text.Length);
        editor.Text = _lastText;
        editor.SelectionStart = loc;
    }
    else
    {
        _lastText = editor.Text.Insert(loc, text);
        editor.Text = _lastText;
        editor.SelectionStart = loc + text.Length;
    }
}

We can now implement event handlers for Undo and Redo. We can obtain the description of the edit from the stack of editing history for an Undo, or from the stack of undo history for a Redo. This description gives us the type of edit (i.e., either insertion or deletion), the beginning position of the edit, and the inserted or deleted string. To implement a Redo, we simply do this edit, but to implement an Undo, we must do the opposite.

Parenthesis Matching

The problem of finding matching parentheses must be solved in many computing applications. For example, consider a C# compiler. Matching parentheses (( and )), brackets ([ and ]), and braces ({ and }) delimit various parts of the source code. In order for these parts to be interpreted correctly, the compiler must be able to determine how these different kinds of parentheses match up with each other. Another example is processing structured data stored in XML format. Different parts of such a data set are delimited by nested begin tags like <summary> and end tags like </summary> (documentation comments in C# code are in XML format). These tags are essentially different kinds of parentheses that need to be matched.

We will restrict our attention to parentheses, brackets, and braces. We will call all six of these characters “parentheses”, but will divide them into three types. Each type then has an opening parenthesis and a closing parenthesis. We will define a string restricted to these six characters to be matched (or balanced) if we can repeatedly remove an opening parenthesis and a closing parenthesis of the same type to its immediate right until there are no more parentheses.

For example, suppose we have the string, “([]{()[]})[{}]”. We can apply the matching-pair removal process described above as follows (blank space is inserted to make it easier to see which parentheses are removed):

    ([]{()[]})[{}]
    (  {()[]})[{}]
    (  {  []})[{}]
    (  {    })[{}]
    (        )[{}]
              [{}]
              [  ]

Hence, this string is matched. On the other hand, consider the string, “([]{()[])}[{}]”. When we apply the above process to this string, we obtain:

    ([]{()[])}[{}]
    (  {()[])}[{}]
    (  {  [])}[{}]
    (  {    )}[{}]
    (  {    )}[  ]
    (  {    )}

and we can go no further. Hence, this string is not matched.

We can extend the definition of a matched string to include other characters if we first remove all other characters before we begin the matching-pair removal process. In what follows, we will focus on the problem of determining whether a given string is matched.

The matching-pair removal process shown above gives us an algorithm for determining whether a string is matched. However, if implemented directly, it isn’t very efficient. Changes to a string are inefficient because the entire string must be reconstructed. We could use a StringBuilder, but even then, removing characters is inefficient, as all characters to the right of the removed character must be moved to take its place. Even if we simply change parentheses to blanks, as we did in the above example, searching for matching pairs is still rather expensive.

What we would like to do instead is to find a way to apply the matching-pair removal process while scanning the string once. As we are scanning the string, we don’t want to spend time searching for a matching pair. We can do this if, while scanning the string, we keep all unmatched opening parentheses in a stack. Then the parenthesis at the top of the stack will always be the rightmost unmatched opening parenthesis. Thus, starting with an empty stack, we do the following for each character in the string:

If the character is a opening parenthesis, push it onto the stack.
If the character is a closing parenthesis:
- If the stack is nonempty, and the current character matches the character on top of the stack, remove the character from the top of the stack.
- Otherwise, the string is not matched.
Ignore all other characters.

If the stack is empty when the entire string has been processed, then the string is matched; otherwise, it is not.

For example, consider the string, “{a[b]([c]){de}}f[(g)]”. In what follows, we will simulate the above algorithm, showing the result of processing each character on a separate line. The portion of the line with an orange background will be the stack contents, with the top element shown at the right. We will insert blank space in the orange area for clarity, but the stack will only contain opening parentheses. The first character with a gray background is the character currently being processed.

{a[b]([c]){de}}f[(g)]    --- an opening parenthesis - push it onto the stack
{a[b]([c]){de}}f[(g)]    --- ignore
{ [b]([c]){de}}f[(g)]    --- push onto stack
{ [b]([c]){de}}f[(g)]    --- ignore
{ [ ]([c]){de}}f[(g)]    --- closing parenthesis that matches the top - remove top
{    ([c]){de}}f[(g)]    --- push onto stack
{    ([c]){de}}f[(g)]    --- push onto stack
{    ([c]){de}}f[(g)]    --- ignore
{    ([ ]){de}}f[(g)]    --- a match - remove top
{    (   ){de}}f[(g)]    --- a match - remove top
{         {de}}f[(g)]    --- push onto stack
{         {de}}f[(g)]    --- ignore
{         { e}}f[(g)]    --- ignore
{         {  }}f[(g)]    --- a match - remove top
{             }f[(g)]    --- a match - remove top
               f[(g)]    --- ignore
                [(g)]    --- push onto stack
                [(g)]    --- push onto stack
                [(g)]    --- ignore
                [( )]    --- a match - remove top
                [   ]    --- a match - remove top
                         --- end of string and stack empty - matched string

If at any time during the above process we had encountered a closing parenthesis while the stack was empty, this would have indicated that this closing parenthesis has no matching opening parenthesis. In this case, we would have stopped immediately, determining that the string is not matched. Likewise, if we had encountered a closing parenthesis that did not match the parenthesis at the top of the stack, this would have indicated a mismatched pair. Again, we would have stopped immediately. Finally, if we had reached the end of the string with a nonempty stack, this would have indicated that we had at least one opening parenthesis that was never matched. We would have again determined that the string is not matched.

Implementing a Stack

This section gives an overview of perhaps the most common way to implement a stack. For example, the implementations of both System.Collections.Stack and System.Collections.Generic.Stack<T> use this technique. This implementation uses an array to store the elements of the stack, and is quite similar to the StringBuilder implementation we described in the last chapter. We have discussed two kinds of stacks in this chapter - stacks of object?s and generic stacks. We will focus on implementing a generic stack in this section, as it is easy to modify such an implementation to be non-generic.

We first need to consider how to define a generic class. In the simplest case, we simply add a type parameter to the class statement, as follows:

public class Stack<T>
{
    . . .
}

Within this class definition, T is treated like any other type, except that the compiler knows nothing about it. We can declare fields, parameters, and local variables to be of type T. Even though the compiler knows nothing about T, it will still do type checking - you cannot assign an expression of any other type to a variable of type T, and you can only assign an expression of type T to variables of either type T or type object? (because any type is a subtype of object?). Assigning an expression of type T to an object variable may generate a compiler warning, but is permitted as well. In general, we can define generic data types with any number of type parameters if more that one generic type is needed by the data structure. To do this, we would list the type parameters, separated by commas, between the < and > symbols of the generic class definition. Each of the type parameters is then treated as a type within the class definition. We will show how the types passed as type parameters can be restricted in a later section.

For the class Stack<T>, only one type parameter is needed. The type parameter T denotes the type of the values that are stored in the stack. Therefore, the array in which we will store the elements will be of type T?[ ]. The ? is needed because if a reference type is used for T, when the array is constructed, all locations will initially store null, and will continue to store null until stack elements are placed into them.

Note

In the section, “Reference Types and Value Types”, we explained how the ? operator behaves differently depending on whether the underlying type is a reference type or a value type. Because a type parameter might represent either a reference type or a value type, we need to address how this operator behaves for a type parameter. Similar to its behavior for a reference type, when this operator is used with a type parameter, the code produced is unchanged. Instead, it is simply an annotation indicating that null values may be present. Note that this can happen only if the underlying type happens to be a reference type.

As in the StringBuilder implementation, we will need a private field for this array. This field can be initialized in a manner similar to the StringBuilder implementation; hence, we don’t need to write a constructor.

A stack has a public read-only property, Count, which gets the number of elements in the stack (as an int). We can define this property to use the default implementation with a private set accessor, as outlined in the section, “Properties”.

Before we can delve any further into the implementation, we need to decide how we are going to arrange the elements in the array. Because all of our accesses will be to the top of the stack, it makes sense to keep the bottom element of the stack at location 0, and as we go up the stack, keep each successive element in the next location:

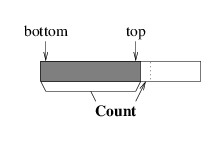
This arrangement makes sense because unless all of the array locations are being used, there is room to push a new element on top of the stack without having to move any pre-existing elements out of its way.

Note the similarity of this arrangement to the implementation of a StringBuilder. Given this similarity, we can implement the Push method in a similar way to how we implemented the Append method for a StringBuilder. Instead of taking a char parameter, the Push method takes a T parameter, but this is the type that we can store in the array. The biggest difference in these two methods is that while Append returns a StringBuilder, Push returns nothing.

We now need to implement the public methods that retrieve elements from the stack. We will start with the Peek method, which takes no parameters and returns a T. This method needs to begin with some error checking: if there are no elements in the stack, it needs to throw an InvalidOperationException. We can do this by constructing such an exception and throwing it with the throw keyword:

throw new InvalidOperationException();

If there are elements in the stack, we need to return the one at the top. Note from the figure above that the top element is at the location preceding the location indexed by Count. However, note that this element is of type T?, whereas the return type of Peek is T. Thus, returning this element will generate a warning unless we use the ! operator. This operator is safe to use here because the location we are returning stores an element that was passed to Push as type T.

Note

Note that because T can represent any type, it is possible that it represents a nullable type; for example, it is permissible to define a Stack<string?>. Therefore, it is possible that the element being returned is null. However, we don’t need to concern ourselves with this case, as it will be handled by the calling code. The point is that we are returning something of type T, even if T represents a non-nullable reference type.

The other public method to retrieve an element is the Pop method. This method also takes no parameters and returns a T. Part of what it does we have already implemented in the Peek method. In order to avoid duplicating code, we can retrieve the top element using the Peek method, and save it in a local variable so that we can return it when we are finished with this method (avoiding code duplication improves maintainability, as there are fewer places that might need to be modified later). Note that by using the Peek method, we are taking advantage of the fact that it checks whether the stack is empty; hence, there is no need to do that here. Before we can return the value we retrieved, we need to update Count to reflect the fact that we are removing one element.

While what we have described in the preceding paragraph is sufficient for correct functioning, there is one issue we need to address. Note that we have done nothing to the array location that stored the value we popped - it still stores that value. This fact does not impact correctness, however, because after we update the number of elements, we are no longer considering that location to be storing a stack element - its contents are irrelevant. Nevertheless, there is a performance issue here. If T is a reference type, then the reference stored in this location may refer to a large data structure that is no longer needed by the program. Because this array location still stores a reference to it, the garbage collector cannot tell that it is no longer in use, and consequently, it cannot reclaim the storage.

It therefore makes sense to remove what is stored in this array location. However, we run into a difficulty when we try to do this. We can’t simply assign null to this location because T might be a value type; hence, the compiler will not allow such an assignment. In order to address this problem, C# has the keyword, default, which can be used to get the default value for a given type. Thus, if T is a reference type, default(T) will give us null, but if T is a value type, it will give us the value whose binary representation is all 0s. In order to free up any memory we might no longer need, it therefore makes sense to assign default(T) to an array location after we are no longer using it.

Tip

Often the parameter to default (including the parentheses) can be omitted because the compiler can detect what type is needed. This is the case in the current context. If using default without the parameter gives a syntax error, supply the parameter.

Finally, we can implement a public Clear method. This method takes no parameters and returns nothing. One way to implement it would be to pop all of the elements, one by one, from the stack. However, this could be very inefficient if the stack contains a lot of elements. A better way is simply to change Count to 0; however, this way prevents the garbage collector from reclaiming storage we no longer need. In order to allow this storage to be reclaimed, we should also replace our array with a new array of the size we used when we initialized this field (note that this is more efficient than replacing every element with the default element of the appropriate type). Because we are no longer using the old array, the garbage collector can reclaim it, along with any otherwise unused data it might refer to.

Due to the similarities between this implementation and the StringBuilder implementation, the two data structures have similar performance characteristics. In fact, it is possible to show that any sequence of n operations on an initially empty Stack<T> is done in O(n) time - i.e., in time proportional to n.

Introduction to Queues

Stacks provide LIFO access to data, but sometimes we need first-in-first-out, or FIFO, access. Consider, for example, the computation of capital gains from stock sales. Typically an investor will buy shares of a stock commodity at various times and for different prices. When shares are sold, the amount of money received doesn’t depend on which shares of a given commodity are sold, as each share is worth the same amount at that time. Likewise, the unsold shares of that commodity each have the same value. However, for accounting purposes, it does matter. Specifically, the capital gain for that sale is defined to be the amount received from the sale minus the amount originally paid for those shares, assuming the shares sold are the oldest shares of that commodity owned by the investor.

Suppose now that we want to compute the capital gains from sales of stock. As shares are purchased, we need to record the purchase price of each share, along with the order in which the shares were purchased. As shares are sold, we need to retrieve the original purchase price of the oldest shares of each commodity sold. We therefore need first-in-first-out access to the purchase prices of the shares of each commodity owned. To keep this relatively simple, in what follows we will assume that we only need to keep track of one stock commodity.

A queue provides FIFO access to data items. Like a stack, a queue is a sequence of data items. However, a queue behaves more like a line of people at a ticket counter. Each person who enters the queue enters at the back, and the next person who is served is the person at the front. Thus, the people in the queue are served in FIFO order. Likewise, new data items are added to the back of a queue, and data items are retrieved from the front.

.NET provides both a non-generic queue of object?s (System.Collections.Queue) and a generic queue (System.Collections.Generic.Queue<T>). For simplicity, we will focus on the generic version. The non-generic version is the same, except that wherever the type parameter T is used in the generic version, object? is used in the non-generic version.

Like Stack<T>, Queue<T> has a public constructor that takes no parameters and constructs an empty queue, along with a public Count property that gets the number of elements in the queue (as an int). It also has the following public methods:

An Enqueue method that takes a single parameter of type T and places it at the back of the queue.
A Peek method that takes no parameters and returns the element (of type T) at the front of the queue without changing the queue’s contents. If the queue is empty, this method throws an InvalidOperationException.
A Dequeue method, which takes no parameters and removes and returns the element at the front of the queue. If the queue is empty, this method throws an InvalidOperationException.

To implement a capital gain calculator using a Queue<T>, we first need to determine what type to make the elements. We will need to store the purchase price of each share we buy in the queue. An appropriate type for storing monetary amounts is the decimal type. Therefore, we will use an initially empty Queue<decimal>. Each time we buy shares, we enqueue the purchase price of each share onto the queue. When we sell shares, we need to compute the sum of the capital gains for all of the shares we sold. To get the capital gain for a single share, we dequeue its original purchase price from the queue, and subtract that purchase price from the selling price. Using the queue in this way ensures that we sell the shares in FIFO order.

Implementing a Queue

We will approach the implementation of a queue much like we did the implementation of a stack - we will use part of an array to store the elements, and create a larger array as needed. However, efficiently implementing a stack is easier because we only need to access one end of a stack, but we need to access both ends of a queue. Suppose, for example, that we were to use the initial part of the array, as we did for a stack; i.e.:

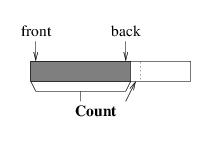
$A queue implementation using the initial part of an\narray$ $A queue implementation using the initial part of an\narray$

This implementation works well as long as we are only enqueuing elements — each element is placed at the back, much like pushing an element onto a stack. However, consider what happens when we dequeue an element. The element is easy to locate, as it must be at index 0, but in order to maintain the above picture, we would need to move all of the remaining elements one location to the left. This becomes less efficient as the number of elements in the queue increases.

One alternative is to modify the picture somewhat:

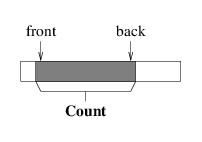
We can maintain this picture more efficiently, as there is now no need to move the elements when we dequeue an element. It does mean that we need to keep track of a bit more information, namely, the location of either the front or the back, in addition to the Count (note that we can compute the other end from these two values). But a more serious problem remains. Notice that as we enqueue and dequeue elements, the portion of the array that we are using works its way to the right. Eventually, the back element will be the last element in the array. However, this doesn’t mean that we are using the entire array, as the front can be anywhere in the array.

To solve this problem, when we need to enqueue an element but the back element is in the last array location, we place the next element at index 0. It is as if we are imagining the array as being circular, as the next location after the last is back at the beginning. The following picture gives two views of such a “circular array” implementation:

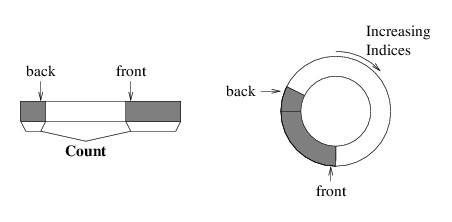
With this implementation, we only need to construct a larger array if we completely fill the current array, and unless we need to do this, we don’t need to move elements around. We need the following class members in order to keep track of everything:

a private T?[ ] field in which to store the elements;
a public int Count property; and
a private int field giving the index of the element at the front of the queue (if the queue is empty, this can be any valid index).

Let us now consider how we would implement Enqueue. We first need to determine whether the array is full by comparing the Count with the size of the array. If it is full, we need to construct a new array of twice the size, as we did for both the StringBuilder implementation and the stack implementation. However, we can’t simply copy the entire array to the beginning of the new array, as we did for these other two implementations. To do so would leave a gap in the middle of the queue, as shown in the following illustration:

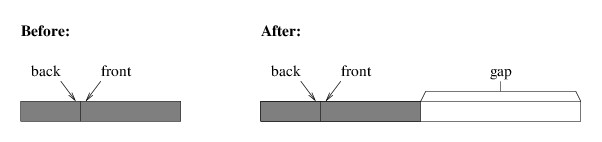
$Why a simple copy will not work for a circular\narray$ $Why a simple copy will not work for a circular\narray$

While there are several ways of copying the elements correctly, it may be helpful to copy in such a way that the index of the front of the queue remains unchanged; i.e., we copy as follows:

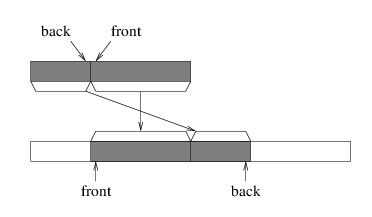
In order to copy the elements like this, we can use the static method, Array.Copy. This method takes the following parameters:

The array to copy from.
An int giving the index of the first element to copy.
The array to copy to.
An int giving the index in which to place the first element.
An int giving the number of elements to copy.

Just figuring out how to fill in these parameters takes some work. Let’s first consider the part that begins with the front of the queue. The index of the first element to copy is the index of the front of the queue, which we have in a private field. We want to place this element at the same index in the new array. In order to compute the number of elements to copy, first observe that we know the number of elements in the original array (we can use either the Count property or the length of this array, as these values are equal whenever we need a larger array). To get the number of elements we want to copy, we can subtract from this value the number of elements we are not copying — i.e., the number of elements preceding the index of the front of the queue. The number of elements preceding any index i is always i; hence, by subtracting the index of the front of the queue from the Count, we get the number of elements we are copying by this call.

Now let’s see if we can figure out the parameters for the other call. The first element we want to copy is at index 0. We want to place it immediately following the elements we have already copied. Because the last of these elements occupies the last index of the original array, whose size is currently the same as the Count, the next index is just the Count. The number of elements we want to copy, as we have already argued, is the index of the front of the queue.

Once we have the elements copied to the new array, the hardest part is done. After we do this, we just need to copy the reference to the new array into the array field.

Once we have ensured that there is room in the array to add a new element, we can complete the Enqueue method. We need to place the element at the back of the queue. We can obtain the proper location by adding the Count to the index of the front of the queue, provided this value is not beyond the end of the array. If it is, then we need to wrap it around by subtracting the length of the array. We can then increment the number of elements, and we are (finally) done.

The Peek method is straightforward — after verifying that the queue is nonempty, we simply return the element at the front. The Dequeue method isn’t much more difficult. We can obtain the element we want to return using the Peek method. We then need to place the default element of type T at the front, and update both the index of the front of the queue and the Count before returning the element we obtained ealier from Peek. The only slightly tricky part is making sure that when we update the index of the front of the queue, we don’t go outside of the array. If we do, we need to wrap it back around to 0.

Stacks and Queues