Binary Trees

A binary tree is a tree in which each node has exactly two children, either of which may be empty. For example, the following is a binary tree:

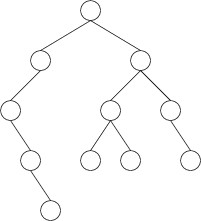
Note that some of the nodes above are drawn with only one child or no children at all. In these cases, one or both children are empty. Note that we always draw one child to the left and one child to the right. As a result, if one child is empty, we can always tell which child is empty and which child is not. We call the two children the left child and the right child.

We can implement a single node of a binary tree as a data structure and use it to store data. The implementation is simple, like the implementation of a linked list cell. Let’s call this type BinaryTreeNode<T>, where T will be the type of data we will store in it. We need three public properties:

• a Data property of type T;
• a LeftChild property of type BinaryTreeNode<T>?; and
• a RightChild property of type BinaryTreeNode<T>?.

We can define both get and set accessors using the default implementation for each of these properties. However, it is sometimes advantageous to make this type immutable. In such a case, we would not define any set accessors, but we would need to be sure to define a constructor that takes three parameters to initialize these three properties. While immutable nodes tend to degrade the performance slightly, they also tend to be easier to work with. For example, with immutable nodes it is impossible to build a structure with a cycle in it.

Introduction to Binary Search Trees

In this section and the next, we will present a binary search tree as a data structure that can be used to implement a dictionary whose key type can be ordered. This implementation will provide efficient lookups, insertions, and deletions in most cases; however, there will be cases in which the performance is bad. In a later section, we will show how to extend this good performance to all cases.

A binary search tree is a binary tree containing key-value pairs whose keys can be ordered. Furthermore, the data items are arranged such that the key in each node is:

• greater than all the keys in its left child; and
• less than all the keys in its right child.

Note that this implies that all keys must be unique. For example, the following is a binary search tree storing integer keys (only the keys are shown):

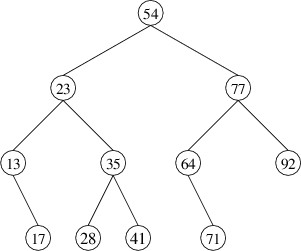
The hierarchical nature of this structure allows us to do something like a binary search to find a key. Suppose, for example, that we are looking for 41 in the above tree. We first compare 41 with the key in the root. Because 41 < 54, we can safely ignore the right child, as all keys there must be greater than 54. We therefore compare 41 to the key in the root of the left child. Because 41 > 23, we look in the right child, and compare 41 to 35. Because 41 > 35, we look in the right child, where we find the key we are looking for.

Note the similarity of the search described above to a binary search. It isn’t exactly the same, because there is no guarantee that the root is the middle element in the tree — in fact, it could be the first or the last. In many applications, however, when we build a binary search tree as we will describe below, the root of the tree tends to be roughly the middle element. When this is the case, looking up a key is very efficient. Later, we will show how we can build and maintain a binary search tree so that this is always the case.

It isn’t hard to implement the search strategy outlined above using a loop. However, in order to reinforce the concept of recursion as a tree processing technique, let’s consider how we would implement the search using recursion. The algorithm breaks into four cases:

• The tree is empty. In this case, the element we are looking for is not present.
• The key we are looking for is at the root - we have found what we are looking for.
• The key we are looking for is less than the key at the root. We then need to look for the given key in the left child. Because this is a smaller instance of our original problem, we can solve it using a recursive call.
• The key we are looking for is greater than the key at the root. We then look in the right child using a recursive call.

If we need to compare elements using a CompareTo method, it would be more efficient to structure the code so that this method is only called once; e.g.,

• If the tree is empty . . . .
• Otherwise:
  • Get the result of the comparison.
  • If the result is 0 . . . .
  • Otherwise, if the result is negative . . . .
  • Otherwise . . . .

This method would need to take two parameters — the key we are looking for and the tree we are looking in. This second parameter will actually be a reference to a node, which will either be the root of the tree or null if the tree is empty. Because this method requires a parameter that is not provided to the TryGetValue method, this method would be a private method that the TryGetValue method can call. This private method would then return the node containing the key, or null if this key was not found. The TryGetValue method can be implemented easily using this private method.

We also need to be able to implement the Add method. Let’s first consider how to do this assuming we are representing our binary search tree with immutable nodes. The first thing to observe is that because we can’t modify an immutable node, we will need to build a binary search tree containing the nodes in the current tree, plus a new node containing the new key and value. In order to accomplish this, we will describe a private recursive method that returns the result of adding a given key and value to a given binary search tree. The Add method will then need to call this private method and save the resulting tree.

We therefore want to design a private method that will take three parameters:

• a binary search tree (i.e., reference to a node);
• the key we want to add; and
• the value we want to add.

It will return the binary search tree that results from adding the given key and value to the given tree.

This method again has four cases:

• The tree is empty. In this case, we need to construct a node containing the given key and value and two empty children, and return this node as the resulting tree.
• The root of the tree contains a key equal to the given key. In this case, we can’t add the item - we need to throw an exception.
• The given key is less than the key at the root. We can then use a recursive call to add the given key and value to the left child. The tree returned by the recursive call needs to be the left child of the result to be returned by the method. We therefore construct a new node containing the data and right child from the given tree, but having the result of the recursive call as its left child. We return this new node.
• The given key is greater than the key at the root. We use a recursive call to add it to the right child, and construct a new node with the result of the recursive call as its right child. We return this new node.

Note that the above algorithm only adds the given data item when it reaches an empty tree. Not only is this the most straightforward way to add items, but it also tends to keep paths in the tree short, as each insertion is only lengthening one path. This page contains an application that will show the result of adding a key at a time to a binary search tree.

The above algorithm can be implemented in the same way if mutable binary tree nodes are used; however, we can improve its performance a bit by avoiding the construction of new nodes when recursive calls are made. Instead, we can change the child to refer to the tree returned. If we make this optimization, the tree we return will be the same one that we were given in the cases that make recursive calls. However, we still need to construct a new node in the case in which the tree is empty. For this reason, it is still necessary to return the resulting tree, and we need to make sure that the Add method always uses the returned tree.

Removing from a Binary Search Tree

Before we can discuss how to remove an element from a binary search tree, we must first define exactly how we want the method to behave. Consider first the case in which the tree is built from immutable nodes. We are given a key and a binary search tree, and we want to return the result of removing the element having the given key. However, we need to decide what we will do if there is no element having the given key. This does not seem to be exceptional behavior, as we may have no way of knowing in advance whether the key is in the tree (unless we waste time looking for it). Still, we might want to know whether the key was found. We therefore need two pieces of information from this method - the resulting tree and a bool indicating whether the key was found. In order to accommodate this second piece of information, we make the bool an out parameter.

We can again break the problem into cases and use recursion, as we did for adding an element. However, removing an element is complicated by the fact that its node might have two nonempty children. For example, suppose we want to remove the element whose key is 54 in the following binary search tree:

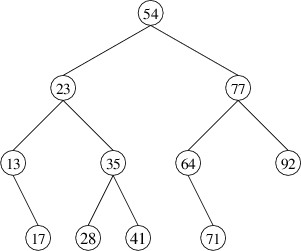
In order to preserve the correct ordering of the keys, we should replace 54 with either the next-smaller key (i.e., 41) or the next-larger key (i.e., 64). By convention, we will replace it with the next-larger key, which is the smallest key in its right child. We therefore have a sub-problem to solve - removing the element with the smallest key from a nonempty binary search tree. We will tackle this problem first.

Because we will not need to remove the smallest key from an empty tree, we don’t need to worry about whether the removal was successful - a nonempty binary search tree always has a smallest key. However, we still need two pieces of information from this method:

• the element removed (so that we can use it to replace the element to be removed in the original problem); and
• the resulting tree (so that we can use it as the new right child in solving the original problem).

We will therefore use an out parameter for the element removed, and return the resulting tree.

Because we don’t need to worry about empty trees, and because the smallest key in a binary search tree is never larger than the key at the root, we only have two cases:

• The left child is empty. In this case, there are no keys smaller than the key at the root; i.e., the key at the root is the smallest. We therefore assign the data at the root to the out parameter, and return the right child, which is the result of removing the root.
• The left child is nonempty. In this case, there is a key smaller than the key at the root; furthermore, it must be in the left child. We therefore use a recursive call on the left child to obtain the result of removing the element with the smallest key from that child. We can pass as the out parameter to this recursive call the out parameter that we were given - the recursive call will assign to it the element removed. Because our nodes are immutable, we then need to construct a new node whose data and right child are the same as in the given tree, but whose left child is the tree returned by the recursive call. We return this node.

Having this sub-problem solved, we can now return to the original problem. We again have four cases, but one of these cases breaks into three sub-cases:

• The tree is empty. In this case the key we are looking for is not present, so we set the out parameter to false and return an empty tree.
• The key we are looking for is at the root. In this case, we can set the out parameter to true, but in order to remove the element, we have three sub-cases:
  • The left child is empty. We can then return the right child (the result of removing the root).
  • The right child is empty. We can then return the left child.
  • Both children are nonempty. We must then obtain the result of removing the smallest key from the right child. We then construct a new node whose data is the element removed from the right child, the left child is the left child of the given tree, and the right child is the result of removing the smallest key from that child. We return this node.
• The key we are looking for is less than the key at the root. We then obtain the result of removing this key from the left child using a recursive call. We can pass as the out parameter to this recursive call the out parameter we were given and let the recursive call set its value. We then construct a new node whose data and right child are the same as in the given tree, but whose left child is the tree returned by the recursive call. We return this node.
• The key we are looking for is greater than the key at the root. This case is symmetric to the above case.

As we did with adding elements, we can optimize the methods described above for mutable nodes by modifying the contents of a node rather than constructing new nodes.

Inorder Traversal

When we store keys and values in an ordered dictionary, we typically want to be able to process the keys in increasing order. The “processing” that we do may be any of a number of things - for example, writing the keys and values to a file or adding them to the end of a list. Whatever processing we want to do, we want to do it increasing order of keys.

If we are implementing the dictionary using a binary search tree, this may at first seem to be a rather daunting task. Consider traversing the keys in the following binary search tree in increasing order:

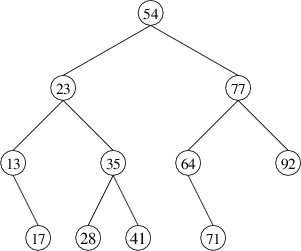
Processing these keys in order involves frequent jumps in the tree, such as from 17 to 23 and from 41 to 54. It may not be immediately obvious how to proceed. However, if we just think about it with the purpose of writing a recursive method, it actually becomes rather straightforward.

As with most tree-processing algorithms, if the given tree is nonempty, we start at the root (if it is empty, there are no nodes to process). However, the root isn’t necessarily the first node that we want to process, as there may be keys that are smaller than the one at the root. These key are all in the left child. We therefore want to process first all the nodes in the left child, in increasing order of their keys. This is a smaller instance of our original problem - a recursive call on the left child solves it. At this point all of the keys less than the one at the root have been processed. We therefore process the root next (whatever the “processing” might be). This just leaves the nodes in the right child, which we want to process in increasing order of their keys. Again, a recursive call takes care of this, and we are finished.

The entire algorithm is therefore as follows:

• If the given tree is nonempty:
  • Do a recursive call on the left child to process all the nodes in it.
  • Process the root.
  • Do a recursive call on the right child to process all the nodes in it.

This algorithm is known as an inorder traversal because it processes the root between the processing of the two children. Unlike preorder traversal, this algorithm only makes sense for binary trees, as there must be exactly two children in order for “between” to make sense.