Introduction to Tries
Introduction to Tries
A trie is a nonempty tree storing a set of words in the following way:
- Each child of a node is labeled with a character.
- Each node contains a boolean indicating whether the labels in the path from the root to that node form a word in the set.
The word, “trie”, is taken from the middle of the word, “retrieval”, but to avoid confusion, it is pronounced like “try” instead of like “tree”.
Suppose, for example, that we want to store the following words:
- ape
- apple
- cable
- car
- cart
- cat
- cattle
- curl
- far
- farm
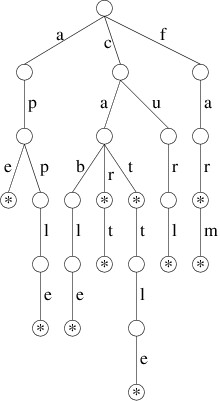
A trie storing these words (where we denote a value of true for the
boolean with a *) is as follows:
Thus, for example, if we follow the path from the root through the
labels ‘c’, ‘a’, and ‘r’, we reach a node with a true boolean value
(shown by the * in the above picture); hence, “car” is in this set of
words. However, if we follow the path through the labels ‘c’, ‘u’, and
‘r’, the node we reach has a false boolean; hence, “cur” is not in
this set. Likewise, if we follow the path through ‘a’, we reach a node
from which there is no child labeled ‘c’; hence, “ace” is not in this
set.
Note that each subtree of a trie is also a trie, although the “words” it stores may begin to look a little strange. For example if we follow the path through ‘c’ and ‘a’ in the above figure, we reach a trie that contains the following “words”:
- “ble”
- “r”
- “rt”
- “t”
- “ttle”
These are actually the completions of the original words that begin with the prefix “ca”. Note that if, in this subtree, we take the path through ’t’, we reach a trie containing the following completions:
- "" [i.e., the empty string]
- “tle”
In particular, the empty string is a word in this trie. This motivates an alternative definition of the boolean stored in each node: it indicates whether the empty string is stored in the trie rooted at this node. This definition may be somewhat preferable to the one given above, as it does not depend on any context, but instead focuses entirely on the trie rooted at that particular node.
One of the main advantages of a trie over an AVL tree is the speed with which we can look up words. Assuming we can quickly find the child with a given label, the time we need to look up a word is proportional to the length of the word, no matter how many words are in the trie. Note that in looking up a word that is present in an AVL tree, we will at least need to compare the given word with its occurrence in the tree, in addition to any other comparisons done during the search. The time it takes to do this one comparison is proportional to the length of the word, as we need to verify each character (we actually ignored the cost of such comparisons when we analyzed the performance of AVL trees). Consequently, we can expect a significant performance improvement by using a trie if our set of words is large.
Let’s now consider how we can implement a trie. There are various ways that this can be done, but we’ll consider a fairly straightforward approach in this section (we’ll improve the implementation in the next section). We will assume that the words we are storing are comprised of only the 26 lower-case English letters. In this implementation, a single node will contain the following private fields:
- A bool storing whether the empty string is contained in the trie rooted at this node (or equivalently, whether this node ends a word in the entire trie).
- A 26-element array of nullable tries storing the children, where element 0 stores the child labeled ‘a’, element 1 stores the child labeled ‘b’, etc. If there is no child with some label, the corresponding array element is null.
For maintainability, we should use private constants to store the above array’s size (i.e., 26) and the first letter of the alphabet (i.e., ‘a’). Note that in this implementation, other than this last constant, no chars or strings are
actually stored. We can see if a node has a child labeled by a given
char by finding the difference between that char and and the first letter of the alphabet, and
using that difference as the array index. For example, suppose the array
field is named _children, the constant giving the first letter of the alphabet is _alphabetStart, and label is a char variable
containing a lower-case letter. Because char is technically a
numeric type, we can perform arithmetic with chars; thus, we can
obtain the child labeled by label by retrieving
_children[label - _alphabetStart]. More specifically, if _alphabetStart is ‘a’ and label
contains ’d’, then the difference, label - _alphabetStart, will be 3; hence,
the child with label ’d’ will be stored at index 3. We have therefore
achieved our goal of providing quick access to a child with a given
label.
Let’s now consider how to implement a lookup. We can define a public method for this purpose within the class implementing a trie node:
public bool Contains(string s)
{
. . .
}Note
This method does not need a trie node as a parameter because the method will belong to a trie node. Thus, the method will be able to access the node as this, and may access its private fields directly by their names.
The method consists of five cases:
sis null. Note that even thoughsis not defined to be nullable, because the method is public, user code could still pass a null value. In this case, we should throw an ArgumentNullException, provides more information than does a NullReferenceException.sis the empty string. In this case the bool stored in this node indicates whether it is a word in this trie; hence, we can simply return this bool.- The first character of
sis not a lower-case English letter (i.e., it is less than ‘a’ or greater than ‘z’). The constants defined for this class should be used in making this determination. In this case,scan’t be stored in this trie; hence, we can return false. - The child labeled with the first character of
s(obtained as described above) is missing (i.e., is null). Thensisn’t stored in this trie. Again, we return false. - The child labeled with the first character of
sis present (i.e., non-null). In this case, we need to determine whether the substring following the first character ofsis in the trie rooted at the child we retrieved. This can be found using a recursive call to this method within the child trie node. We return the result of this recursive call.
In order to be able to look up words, we need to be able to build a trie to look in. We therefore need to be able to add words to a trie. It’s not practical to make a trie node immutable, as there is too much information that would need to be copied if we need to replace a node with a new one (we would need to construct a new node for each letter of each word we added). We therefore should provide a public method within the trie node class for the purpose of adding a word to the trie rooted at this node:
public void Add(string s)
{
. . .
}This time there are four cases:
sis null. This case should be handled as in the Contains method above.sis the empty string. Then we can record this word by setting the bool in this node to true.- The first character of
sis not a lower-case English letter. Then we can’t add the word. In this case, we’ll need to throw an exception. - The first character is a lower-case English letter. In this case, we
need to add the substring following the first character of
sto the child labeled with the first letter. We do this as follows:- We first need to make sure that the child labeled with the first letter of
sis non-null. Thus, if this child is null, we construct a new trie node and place it in the array location for this child. - We can now
add the substring following the first letter of
sto this child by making a recursive call.
- We first need to make sure that the child labeled with the first letter of