Truth Tables in Logika

Now that we’ve seen the four basic logic gates and truth tables, we can put them together to build bigger truth tables for longer logical formulae.

Operator precedence

Logical operators have a defined precedence (order of operations) just as arithmetic operators do. In arithmetic, parentheses have the highest precedence, followed by exponents, then multiplication and division, and finally addition and subtraction.

Here is the precedence of the logical operators, from most important (do first) to least important (do last):

Parentheses
Not operator, ¬
And operator, ∧
Or operator, ∨
Implies operator, →

For example, in the statement (p ∨ q) ∧ ¬p, we would evaluate the operators in the following order:

The parentheses (which would resolve the (p ∨ q) expression)
The not, ¬
The and, ∧

Sometimes we have more than one of the same operator in a single statement. For example: p ∨ q ∨ r. Different operators have different rules for resolving multiple occurrences:

Multiple parentheses - the innermost parentheses are resolved first, working from inside out.
Multiple not ( ¬ ) operators – the rightmost ¬ is resolved first, working from right to left. For example, ¬¬p is equivalent to ¬(¬p).
Multiple and ( ∧ ) operators – the leftmost ∧ is resolved first, working from left to right. For example, p ∧ q ∧ r is equivalent to (p ∧ q) ∧ r.
Multiple or ( ∨ ) operators – the leftmost ∨ is resolved first, working from left to right. For example, p ∨ q ∨ r is equivalent to (p ∨ q) ∨ r.
Multiple implies ( → ) operators – the rightmost → is resolved first, working from right to left. For example, p → q → r is equivalent to p → (q → r).

Top-level operator

In a logical statement, the top-level operator is the operator that is applied last (after following the precedence rules above).

For example, in the statement:

p ∨ q → ¬p ∧ r

We would evaluate first the ¬, then the ∧, then the ∨, and lastly the →. Thus the → is the top-level operator.

Classifying truth tables

In our study of logic, it will be convenient to characterize logical formula with a description of their truth tables. We will classify each logical formula in one of three ways:

Tautology - when all truth assignments for a logical formula are true
Contradictory - when all truth assignments for a logical formula are false
Contingent - when some truth assignments for a logical formula are true and some are false.

For example, p ∨ ¬ p is a tautology. Whether p is true or false, p ∨ ¬ p is always true.

On the other hand, p ∧ ¬ p is contradictory. Whether p is true or false, p ∧ ¬ p is always false.

Finally, something like p ∨ q is contingent. When p and q are both false, then p ∨ q is false. However, p ∨ q is true in every other case.

If all truth assignments for a logical formula are True, the formula is said to be a tautology.

Logika syntax

From this point forward, the course will expect you to use Logika formatted truth tables. The Logika truth table for the formula ¬(p ∧ q) is:

      *
-----------------
p q # !(p & q)
-----------------
T T # F T T T
T F # T T F F
F T # T F F T
F F # T F F F
-----------------
Contingent
T: [T F] [F T] [F F]
F: [T T]

Logika truth tables have standard format (syntax) and semantic meanings. All elements of the truth table must be included to be considered correct.

The first line should have a single asterisk (*) over the top-level operator in the formula.
Next is a line of - (minus sign) characters, which must be at least as long as the third line to avoid getting errors.
The third line contains variables | formula. As Logika uses some capital letters as reserved words, you should use lower-case letters as variable names. Additionally, variables should be listed alphabetically.
The fourth line is another row of -, which is the same length as the second line.
Next come the truth assignments. Under the variables, list all possible combinations of T and F. Start with all T and progress linearly to all F. (T and F must be capitalized.) After the Truth assignments is another row of -. Using each truth assignment, fill in truth assignments (T or F) under each operator in the formula in order of precedence (with the top-level operator applied last). Optionally, you can fill in the values for each variable under the forumla (as in the example above). However, it is only required that you fill in the truth assignments under each operator. Be careful to line up the truth assignments DIRECTLY below each operator, as Logika will reject truth tables that aren’t carefully lined up.
Under the truth assignments, put another line of - (minus sign) characters, which should be the same length as the second line.
Finally, classify the formula as either Tautology (if everything under the top-level operator is T), Contradictory (if everything under the top-level operator is F), or Contingent (if there is a mix of T and F under the top-level operator). If the formula is contingent, you must also list which truth assignments made the formula true (i.e., which truth assignments made the top-level operator T) and which truth assignments made the formula false. Follow the image above for the syntax of how to list the truth assignments for contingent examples.

Logical operators in Logika

You may notice that the example above appears to use the ! operator for NOT and the & operator for AND. However, what is shown above demonstrates what we TYPE into Logika, and not what is actually displayed. If we copy and paste the example into a new Logika file, it will look like:

      *
-----------------
p q # ¬(p ∧ q)
-----------------
T T # F T T T
T F # T T F F
F T # T F F T
F F # T F F F
-----------------
Contingent
T: [T F] [F T] [F F]
F: [T T]

Here is a summary of what keys to type in Logika for each traditional logical operator:

Logical operator	What to TYPE in Logika	What you will SEE in Logika
NOT	`!`	`¬`
OR	`\|`	`∨`
AND	`&`	`∧`
IMPLIES	`->:`	`→:`

In the remainder of this book, my examples will be of what you will SEE in Logika.

Example

Suppose we want to write a Logika truth table for:

(p ∧ q) → ¬r

First, we make sure we have a new file in Sireum with the .logika extension. Then, we construct this truth table shell:

                *
----------------------
p q r # (p ∧ q) →: ¬r
----------------------
T T T #
T T F #
T F T #
T F F #
F T T #
F T F #
F F T #
F F F #
----------------------

In the table above, we noticed that the → operator was the top-level operator according to our operator precedence rules.

Next, we fill in the output for the corresponding truth assignment under each operator, from highest precedence to lowest precedence. First, we evaluate the parentheses, which have the highest precedence. For example, we put a T under the ∧ in the first row, as p and q are both T in that row, and T ∧ T is T:

                *
----------------------
p q r # (p ∧ q) →: ¬r
----------------------
T T T #    T
T T F #    T
T F T #    F
T F F #    F
F T T #    F
F T F #    F
F F T #    F
F F F #    F
----------------------

In this example, we are only filling in under each operator (instead of also transcribing over each variable value), but either approach is acceptable.

Next, we fill in under the ¬ operator, which has the next-highest precedence:

                *
----------------------
p q r # (p ∧ q) →: ¬r
----------------------
T T T #    T       F
T T F #    T       T
T F T #    F       F
T F F #    F       T
F T T #    F       F
F T F #    F       T
F F T #    F       F
F F F #    F       T
----------------------

Then, we fill in under our top-level operator, the →. Notice that we must line up the T/F values under the → in the →: symbol. For example, we put a F under the →: on the first row, as (p ∧ q) is T there and ¬r is F, and we know that T→F is F because it describes a broken promise.

                *
----------------------
p q r # (p ∧ q) →: ¬r
----------------------
T T T #    T    F  F
T T F #    T    T  T
T F T #    F    T  F
T F F #    F    T  T
F T T #    F    T  F
F T F #    F    T  T
F F T #    F    T  F
F F F #    F    T  T
----------------------

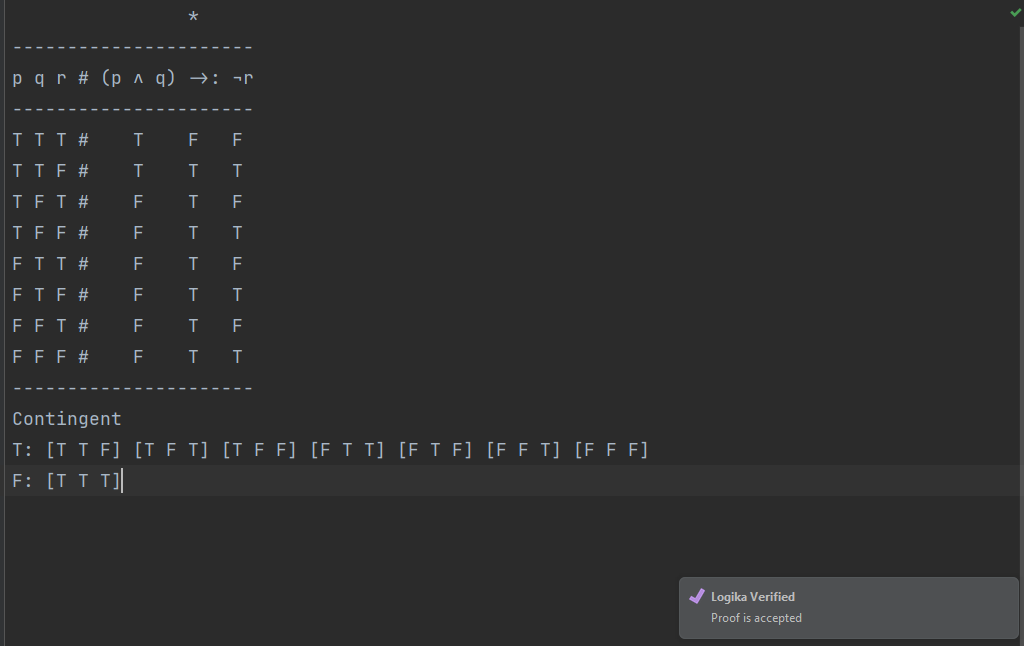
Lastly, we examine the list of outputs under the top-level operator. We see that some truth assignments made the formula true, and that others (one) made the formula false. Thus, the formula is contingent. We label it as such, and list which truth assignments made the formula true and which made it false:

                *
----------------------
p q r # (p ∧ q) →: ¬r
----------------------
T T T #    T    F  F
T T F #    T    T  T
T F T #    F    T  F
T F F #    F    T  T
F T T #    F    T  F
F T F #    F    T  T
F F T #    F    T  F
F F F #    F    T  T
----------------------
Contingent
T: [T T F] [T F T] [T F F] [F T T] [F T F] [F F T] [F F F]
F: [T T T]

If you typed everything correctly, you should see a popup in Sireum logika that says: “Logika Verified” with a purple checkmark:

If you instead see red error markings, hover over them and read the explanations – it means there are errors in your truth table.

If you see no errors and no purple check, you will need to manually run Logika. Right-click in the text area that contains your truth table, and select “Logika Check (All in File)”.