Subsections of Truth Tables
Operators and Circuits
In this chapter, we review basic notions about gates and learn the relationship between circuits and assignment-based computer programs. This sets the stage for analyzing modern programs.
Logical operators
There are four basic logic gates, with corresponding logical operators:
| Meaning | Logical Operator | Logic Gate |
|---|---|---|
| p AND q | p ∧ q | 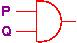
 |
| p OR q | p ∨ q | 
 |
| NOT p | ¬p | 
 |
| p IMPLIES q | p → q | 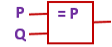
 |
In the above drawings, the input wires are labelled with the names P and Q. The output that is computed is emitted from the rightmost wire which exits the gate. For these simple gates, it is possible to exhaustively test every permutation of potential inputs and summarize results in a table, called a truth table.
Let’s examine the AND gate. The AND gate emits a high voltage (1) exactly when high voltages are sensed at input wires P and Q; otherwise low voltage (0) is emitted. The gate’s physical behavior is summarized by in the following table:
AND: P Q |
-------------
1 1 | 1
1 0 | 0
0 1 | 0
0 0 | 0Truth tables
For the remainder of this course, we will use T (read “true”) for 1 and F (read “false”) for 0. This is because we will examine applications that go far beyond circuit theory and base-two arithmetic. Here are the truth tables for the AND, OR, NOT and IMPLIES gates:
AND: P Q |
-------------
T T | T
T F | F
F T | F
F F | F
OR: P Q |
-------------
T T | T
T F | T
F T | T
F F | F
NOT: P |
-------------
T | F
F | T
IMPLIES: P Q |
-----------------
T T | T
T F | F
F T | T
F F | TA few comments:
The OR gate is inclusive – as long as one of its inputs is true, then its output is true.
You might be confused by the IMPLIES gate. We’ll cover it in detail below.
In the next section, we will learn to write our truth tables in a slightly different format so they can be automatically checked by Sireum Logika.
Implies operator
The implies operator can be difficult to understand. It helps to think of it as a promise: we write P → Q, but we mean If P is true, then I promise that Q will also be true. If we BREAK our promise (i.e., if P is true but Q is false), then the output of an implies gate is false. In every other situation, the output of the implies gate is true.
As a reminder, here is the truth table for the implies operator, → :
P Q | P → Q
-----------------
T T | T
T F | F
F T | T
F F | TIt is likely clear why P → Q is true when both P and Q are true – in this situation, we have kept our promise.
It is also easy to understand why P → Q is false when P is true and Q is false. Here, we have broken our promise – P happened, but Q did not.
In the other two cases for P → Q we have that P is false (and Q is either true or false). Here, P → Q is true simply because we haven’t broken our promise. In these cases, the implication is said to be vacuously true because we have no evidence to prove that it is false.
Circuits
We can also compose the gates to define new operations.
For example, this circuit:
Written ¬(P ∧ Q), defines this computation of outputs:
P Q | ¬(P ∧ Q)
-----------------
T T | F
T F | T
F T | T
F F | TWe can work out the outputs in stages, like this:
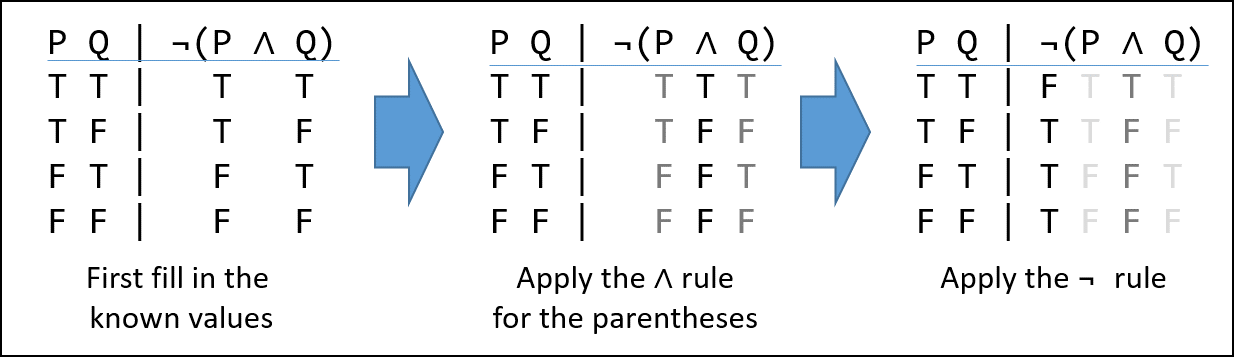
We begin by writing the value of each set of inputs on the left, under their corresponding symbol on the right. Next we apply the operator (gate) with the highest precedence (covered in Operator Precedence in the next section). In our case the () make the AND ( ∧ ) symbol the highest.
A truth assignment is a unique permutation of the possible inputs for a system. For the ∧-gate, it is a 2-variable sequence. Considering the first row we see we have T ∧ T. Looking that up in the ∧-gate truth table we see the result is also “T”, and we record that under the ∧ symbol. We do the same thing all the other truth assignments.
After the initial transcribing of the truth values under their respective variables, we look up the truth-values in the gate tables, not the variables. Also observe that while ∧ is symmetric – i.e. T ∧ F and F ∧ T are both false – the IMPLIES gate is not.
Now we look up the value under the ∧ symbol in the ¬ gate table. In the first row we see that the truth assignment for the first row, “T”, is “F” and record it under the ¬ symbol. Do this for every row and we are done.
Truth Tables in Logika
Now that we’ve seen the four basic logic gates and truth tables, we can put them together to build bigger truth tables for longer logical formulae.
Operator precedence
Logical operators have a defined precedence (order of operations) just as arithmetic operators do. In arithmetic, parentheses have the highest precedence, followed by exponents, then multiplication and division, and finally addition and subtraction.
Here is the precedence of the logical operators, from most important (do first) to least important (do last):
- Parentheses
- Not operator,
¬ - And operator,
∧ - Or operator,
∨ - Implies operator,
→
For example, in the statement (p ∨ q) ∧ ¬p, we would evaluate the operators in the following order:
- The parentheses (which would resolve the
(p ∨ q)expression) - The not,
¬ - The and,
∧
Sometimes we have more than one of the same operator in a single statement. For example: p ∨ q ∨ r. Different operators have different rules for resolving multiple occurrences:
- Multiple parentheses - the innermost parentheses are resolved first, working from inside out.
- Multiple not (
¬) operators – the rightmost¬is resolved first, working from right to left. For example,¬¬pis equivalent to¬(¬p). - Multiple and (
∧) operators – the leftmost∧is resolved first, working from left to right. For example,p ∧ q ∧ ris equivalent to(p ∧ q) ∧ r. - Multiple or (
∨) operators – the leftmost∨is resolved first, working from left to right. For example,p ∨ q ∨ ris equivalent to(p ∨ q) ∨ r. - Multiple implies (
→) operators – the rightmost→is resolved first, working from right to left. For example,p → q → ris equivalent top → (q → r).
Top-level operator
In a logical statement, the top-level operator is the operator that is applied last (after following the precedence rules above).
For example, in the statement:
p ∨ q → ¬p ∧ r
We would evaluate first the ¬, then the ∧, then the ∨, and lastly the →. Thus the → is the top-level operator.
Classifying truth tables
In our study of logic, it will be convenient to characterize logical formula with a description of their truth tables. We will classify each logical formula in one of three ways:
- Tautology - when all truth assignments for a logical formula are true
- Contradictory - when all truth assignments for a logical formula are false
- Contingent - when some truth assignments for a logical formula are true and some are false.
For example, p ∨ ¬ p is a tautology. Whether p is true or false, p ∨ ¬ p is always true.
On the other hand, p ∧ ¬ p is contradictory. Whether p is true or false, p ∧ ¬ p is always false.
Finally, something like p ∨ q is contingent. When p and q are both false, then p ∨ q is false. However, p ∨ q is true in every other case.
If all truth assignments for a logical formula are True, the formula is said to be a tautology.
Logika syntax
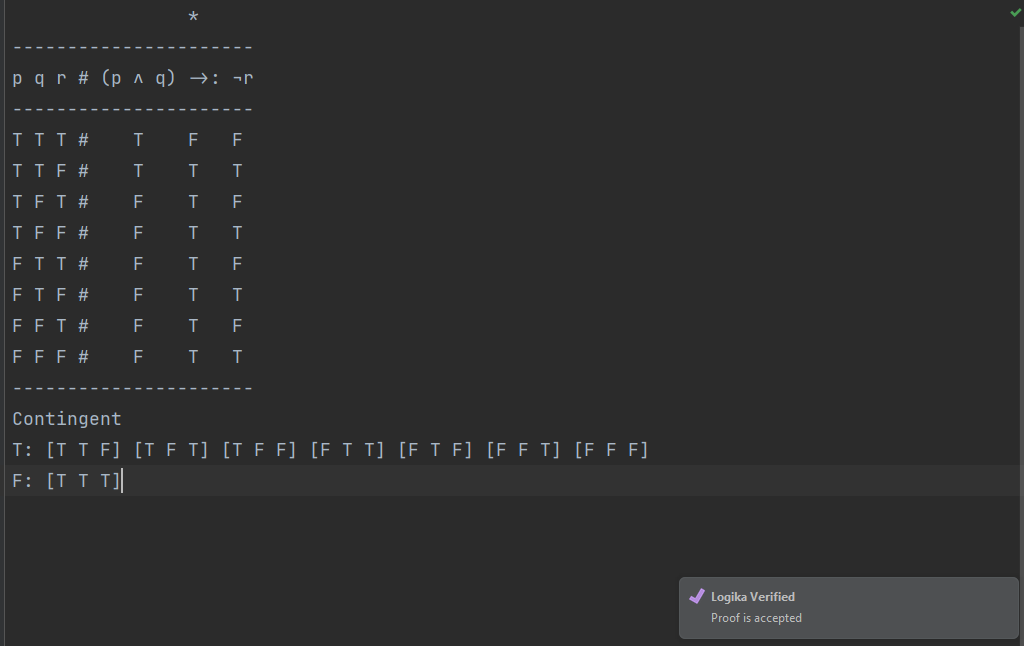
From this point forward, the course will expect you to use Logika formatted truth tables. The Logika truth table for the formula ¬(p ∧ q) is:
*
-----------------
p q # !(p & q)
-----------------
T T # F T T T
T F # T T F F
F T # T F F T
F F # T F F F
-----------------
Contingent
T: [T F] [F T] [F F]
F: [T T]Logika truth tables have standard format (syntax) and semantic meanings. All elements of the truth table must be included to be considered correct.
The first line should have a single asterisk (*) over the top-level operator in the formula.
Next is a line of - (minus sign) characters, which must be at least as long as the third line to avoid getting errors.
The third line contains
variables | formula. As Logika uses some capital letters as reserved words, you should use lower-case letters as variable names. Additionally, variables should be listed alphabetically.The fourth line is another row of -, which is the same length as the second line.
Next come the truth assignments. Under the variables, list all possible combinations of T and F. Start with all T and progress linearly to all F. (T and F must be capitalized.) After the Truth assignments is another row of -. Using each truth assignment, fill in truth assignments (T or F) under each operator in the formula in order of precedence (with the top-level operator applied last). Optionally, you can fill in the values for each variable under the forumla (as in the example above). However, it is only required that you fill in the truth assignments under each operator. Be careful to line up the truth assignments DIRECTLY below each operator, as Logika will reject truth tables that aren’t carefully lined up.
Under the truth assignments, put another line of - (minus sign) characters, which should be the same length as the second line.
Finally, classify the formula as either
Tautology(if everything under the top-level operator is T),Contradictory(if everything under the top-level operator is F), orContingent(if there is a mix of T and F under the top-level operator). If the formula is contingent, you must also list which truth assignments made the formula true (i.e., which truth assignments made the top-level operator T) and which truth assignments made the formula false. Follow the image above for the syntax of how to list the truth assignments for contingent examples.
Logical operators in Logika
You may notice that the example above appears to use the ! operator for NOT and the & operator for AND. However, what is shown above demonstrates what we TYPE into Logika, and not what is actually displayed. If we copy and paste the example into a new Logika file, it will look like:
*
-----------------
p q # ¬(p ∧ q)
-----------------
T T # F T T T
T F # T T F F
F T # T F F T
F F # T F F F
-----------------
Contingent
T: [T F] [F T] [F F]
F: [T T]Here is a summary of what keys to type in Logika for each traditional logical operator:
| Logical operator | What to TYPE in Logika | What you will SEE in Logika |
|---|---|---|
| NOT | ! | ¬ |
| OR | | | ∨ |
| AND | & | ∧ |
| IMPLIES | ->: | →: |
In the remainder of this book, my examples will be of what you will SEE in Logika.
Logika mishandling of implies operator
While the correct order of operations for logical operations is NOT, AND, OR, IMPLIES (from highest precedence to lowest precedence), the Logika tool does not handle the precedence of the implies operator correctly. The characters used for the implies operator in Logika are ->: – however, since Logika takes advantage of Scala’s operator precedence, this means that it interprets an implies operation as having the same (higher) precedence as a minus operation. In this class, we will always use parentheses to force the implies to have the correct precedence.
This incorrect precedence will only be present in our unit on truth tables – other proofs in Logika will use a different operator for implies (__>:) to avoid the issue of being interpreted as a minus operation. (We cannot use __>: in truth tables as the rendering makes the column alignment unclear.)
Example
Suppose we want to write a Logika truth table for:
(p ∧ q) → ¬rFirst, we make sure we have a new file in Sireum with the .logika extension. Then, we construct this truth table shell:
*
----------------------
p q r # (p ∧ q) →: ¬r
----------------------
T T T #
T T F #
T F T #
T F F #
F T T #
F T F #
F F T #
F F F #
----------------------In the table above, we noticed that the → operator was the top-level operator according to our operator precedence rules.
Next, we fill in the output for the corresponding truth assignment under each operator, from highest precedence to lowest precedence. First, we evaluate the parentheses, which have the highest precedence. For example, we put a T under the ∧ in the first row, as p and q are both T in that row, and T ∧ T is T:
*
----------------------
p q r # (p ∧ q) →: ¬r
----------------------
T T T # T
T T F # T
T F T # F
T F F # F
F T T # F
F T F # F
F F T # F
F F F # F
----------------------In this example, we are only filling in under each operator (instead of also transcribing over each variable value), but either approach is acceptable.
Next, we fill in under the ¬ operator, which has the next-highest precedence:
*
----------------------
p q r # (p ∧ q) →: ¬r
----------------------
T T T # T F
T T F # T T
T F T # F F
T F F # F T
F T T # F F
F T F # F T
F F T # F F
F F F # F T
----------------------Then, we fill in under our top-level operator, the →. Notice that we must line up the T/F values under the → in the →: symbol. For example, we put a F under the →: on the first row, as (p ∧ q) is T there and ¬r is F, and we know that T→F is F because it describes a broken promise.
*
----------------------
p q r # (p ∧ q) →: ¬r
----------------------
T T T # T F F
T T F # T T T
T F T # F T F
T F F # F T T
F T T # F T F
F T F # F T T
F F T # F T F
F F F # F T T
----------------------Lastly, we examine the list of outputs under the top-level operator. We see that some truth assignments made the formula true, and that others (one) made the formula false. Thus, the formula is contingent. We label it as such, and list which truth assignments made the formula true and which made it false:
*
----------------------
p q r # (p ∧ q) →: ¬r
----------------------
T T T # T F F
T T F # T T T
T F T # F T F
T F F # F T T
F T T # F T F
F T F # F T T
F F T # F T F
F F F # F T T
----------------------
Contingent
T: [T T F] [T F T] [T F F] [F T T] [F T F] [F F T] [F F F]
F: [T T T]If you typed everything correctly and run a Logika check (Ctrl-Shift-W in Windows and Command-Shift-W on Mac), you should see a popup in Sireum logika that says: “Logika Verified” (yours will not have the purple checkmark, but will have the same text)
If you instead see red error markings, hover over them and read the explanations – it means there are errors in your truth table.
Satisfiability
We say that a logical statement is satisfiable when there exists at least one truth assignment that makes the overall statement true.
In our Logika truth tables, this corresponds to statements that are either contingent or a tautology. (Contradictory statements are NOT satisfiable.)
For example, consider the following truth tables:
*
-----------------------
p q r # p →: q V ¬r ∧ p
-----------------------
T T T # T T F F
T T F # T T T T
T F T # F F F F
T F F # T T T T
F T T # T T F F
F T F # T T T F
F F T # T F F F
F F F # T F T F
------------------------
Contingent
T: [T T T] [T T F] [T F F] [F T T] [F T F] [F F T] [F F F]
F: [T F T]And
*
------------
p # p V ¬p
------------
T # T F
F # T T
-------------
TautologyBoth of these statements are satisfiable, as they have at least one (or more than one) truth assignment that makes the overall statement true.
Logical Equivalence
Two (or more) logical statements are said to be logically equivalent IFF (if and only if, ↔) they have the same truth value for every truth assignment; i.e., their truth tables evaluate exactly the same. (We sometimes refer to this as semantic equivalence.)
An example of logically equivalent statements are q ∧ p and p ∧ (q ∧ p):
*
--------------
p q # (p ∧ q)
--------------
T T # T
T F # F
F T # F
F F # F
---------------
Contingent
T: [T T]
F: [F F] [F T] [T F] *
-------------------
p q # p ∧ (q ∧ p)
-------------------
T T # T T
T F # F F
F T # F F
F F # F F
--------------------
Contingent
T : [T T]
F : [F F] [F T] [T F]In these examples, notice that exactly the same set of truth assignments makes both statements true, and that exactly the same set of truth assignments makes both statements false.
Finding equivalent logical statements of fewer gates (states) is important to several fields. In computer science, fewer states can lead to less memory, fewer operations and smaller programs. In computer engineering, fewer gates means fewer circuits less power and less heat.
Common equivalences
We can similarly use truth tables to show the following common logical equivalences:
- Double negative:
¬ ¬ pandp - Contrapositive:
p → qand¬ q → ¬ p - Expressing an implies using an OR:
p → qand¬ p ∨ q - One of DeMorgan’s laws:
¬ (p ∧ q)and( ¬ p ∨ ¬ q) - Another of DeMorgan’s laws:
¬ (p ∨ q)and( ¬ p ∧ ¬ q)
Expressing additional operators
The bi-implication (↔) and exclusive or (⊕) operators are not directly used in this course. However, we can simulate both operators using a combination of ¬, ∧, ∨, and →:
p ↔ q, which means “p if and only if q”, can be expressed as(p → q) ∧ (q → p)p ⊕ q, which means “p exclusive or q”, can be expressed as(p ∨ q) ∧ ¬(p ∧ q)
Semantic Entailment
Definition
We say a set of premises, p1, p2, …, pn semantically entail a conclusion c, and we write:
p1, p2, ..., pn ⊨ cif whenever we have a truth assignment that makes p1, p2, …, pn all true, then c is also true for that truth assignment.
(Note: we can use the ASCII replacement |= instead of the Unicode ⊨, if we want.)
Showing semantic entailment
Suppose we have premises p ∧ q and p → r. We want to see if these premises necessarily entail the conclusion r ∧ q.
First, we could make truth tables for each premise (being sure to list the variables p, q and r in each case, as that is the overall set of variables in the problem):
//truth table for premise, p ∧ q
*
----------------------
p q r # p ∧ q
----------------------
T T T # T
T T F # T
T F T # F
T F F # F
F T T # F
F T F # F
F F T # F
F F F # F
----------------------
Contingent
T: [T T T] [T T F]
F: [T F T] [T F F] [F T T] [F T F] [F F T] [F F F]//truth table for premise, p → r
*
----------------------
p q r # p →: r
----------------------
T T T # T
T T F # F
T F T # T
T F F # F
F T T # T
F T F # T
F F T # T
F F F # T
----------------------
Contingent
T: [T T T] [T F T] [F T T] [F T F] [F F T] [F F F]
F: [T T F] [T F F]Now, we notice that the truth assignment [T T T] is the only one that makes both premises true. Next, we make a truth table for our potential conclusion, r ∧ q (again, being sure to include all variables used in the problem):
//truth table for potential conclusion, r ∧ q
*
----------------------
p q r # r ∧ q
----------------------
T T T # T
T T F # F
T F T # F
T F F # F
F T T # T
F T F # F
F F T # F
F F F # F
----------------------
Contingent
T: [T T T] [F T T]
F: [T T F] [T F T] [T F F] [F T F] [F F T] [F F F]Here, we notice that the truth assignment [T T T] makes the conclusion true as well. So we see that whenever there is a truth assignment that makes all of our premises true, then that same truth assignment also makes our conclusion true.
Thus, p ∧ q and p → r semantically entail the conclusion r ∧ q, and we can write:
p ∧ q, p → r ⊨ r ∧ qSemantic entailment with one truth table
The process of making separate truth tables for each premise and the conclusion, and then examining each one to see if any truth assignment that makes all the premises true also makes the conclusion true, is fairly tedious.
We are trying to show that IF each premise is true, THEN we promise the conclusion is true. This sounds exactly like an IMPLIES statement, and in fact that is what we can use to simplify our process. If we are trying to show that p1, p2, …, pn semantically entail a conclusion c (i.e., that p1, p2, ..., pn ⊨ c), then we can instead create ONE truth table for the statement:
(p1 ∧ p2 ∧ ... ∧ pn) → c
If this statement is a tautology (which would mean that anytime all the premises were true, then the conclusion was also true), then we would also have that the premises semantically entail the conclusion.
In our previous example, we create a truth table for the statement (p ∧ q) ∧ (p → r) → r ∧ q:
*
--------------------------------------
p q r # (p ∧ q) ∧ (p →: r) →: r ∧ q
--------------------------------------
T T T # T T T T T
T T F # T F F T F
T F T # F F T T F
T F F # F F F T F
F T T # F F T T T
F T F # F F T T F
F F T # F F T T F
F F F # F F T T F
---------------------------------------
TautologyThen we see that it is indeed a tautology.