Associations
Class diagrams also express the associations between classes by drawing lines between the boxes representing them.
There are two basic types of associations we model with UML: has-a and is-a associations. We break these into two further categories, based on the strength of the association, which is either strong or weak. These associations are:
| Association Name | Association Type |
|---|---|
| Realization | weak is-a |
| Generalization | strong is-a |
| Aggregation | weak has-a |
| Composition | strong has-a |
Is-A Associations
Is-a associations indicate a relationship where one class is a instance of another class. Thus, these associations represent polymorphism, where a class can be treated as another class, i.e. it has both its own, and the associated classes’ types.
Realization (Weak is-a)
Realization refers to making an interface “real” by implementing the methods it defines. For C#, this corresponds to a class that is implementing an Interface. We call this a is-a relationship, because the class is treated as being the type of the Interface. It is also a weak relationship as the same interface can be implemented by otherwise unrelated classes. In UML, realization is indicated by a dashed arrow in the direction of implementation:
Generalization
Generalization refers to extracting the shared parts from different classes to make a general base class of what they have in common. For C# this corresponds to inheritance. We call this a strong is-a relationship, because the class has all the same state and behavior as the base class. In UML, generalization is indicated by a solid arrow in the direction of inheritance:
Also notice that we show that Fruit and its Blend() method are abstract by italicizing them.
Has-A Associations
Has-a associations indicates that a class holds one or more references to instances of another class. In C#, this corresponds to having a variable or collection with the type of the associated class. This is true for both kinds of has-a associations. The difference between the two is how strong the association is.
Aggregation
Aggregation refers to collecting references to other classes. As the aggregating class has references to the other classes, we call this a has-a relationship. It is considered weak because the aggregated classes are only collected by the aggregating class, and can exist on their own. It is indicated in UML by a solid line from the aggregating class to the one it aggregates, with an open diamond “fletching” on the opposite side of the arrow (the arrowhead is optional).
Composition
Composition refers to assembling a class from other classes, “composing” it. As the composed class has references to the other classes, we call this a has-a relationship. However, the composing class typically creates the instances of the classes composing it, and they are likewise destroyed when the composing class is destroyed. For this reason, we call it a strong relationship. It is indicated in UML by a solid line from the composing class to those it is composed of, with a solid diamond “fletching” on the opposite side of the arrow (the arrowhead is optional).
Info
Aggregation and composition are commonly confused, especially given they both are defined by holding a variable or collection of another class type. An analogy I like to use to help students reason about the difference is this:
Aggregation is like a shopping cart. When you go shopping, you place groceries into the shopping cart, and it holds them as you push it around the store. Thus, a ShoppingCart class might have a List<Grocery> named Contents, and you would add the items to it. When you reach the checkout, you would then take the items back out. The individual Grocery objects existed before they were aggregated by the ShoppingCart, and also after they were removed from it.
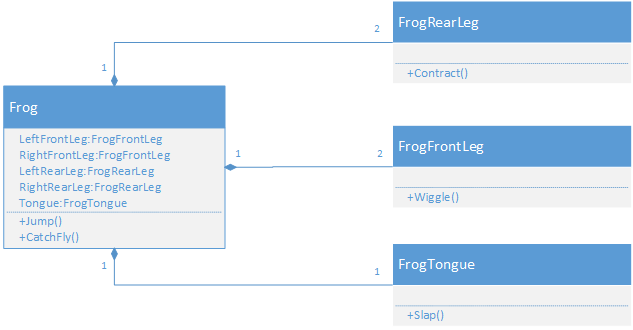
In contrast, Composition is like an organism. Say we create a class representing a Dog. It might be composed of classes like Tongue, Ear, Leg, and Tail. We would probably construct these in the Dog class’s constructor, and when we dispose of the Dog object, we wouldn’t expect these component classes to stick around.
Multiplicity
With aggregation and composition, we may also place numbers on either end of the association, indicating the number of objects involved. We call these numbers the multiplicity of the association.
For example, the Frog class in the composition example has two instances of front and rear legs, so we indicate that each Frog instance (by a 1 on the Frog side of the association) has exactly two (by the 2 on the leg side of the association) legs. The tongue has a 1 to 1 multiplicity as each frog has one tongue.
Multiplicities can also be represented as a range (indicated by the start and end of the range separated by ..). We see this in the ShoppingCart example above, where the count of GroceryItems in the cart ranges from 0 to infinity (infinity is indicated by an asterisk *).
Generalization and realization are always one-to-one multiplicities, so multiplicities are typically omitted for these associations.