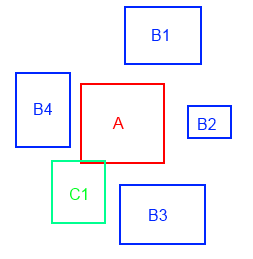
Collision Shapes
Perhaps the most straightforward approach is the use of a collision shape (also called a collision primitive or bounding area). This is a simplified representation of the sprite - simplified in a way that allows for easy mathematical detection of collision events. The collision shape mimics the shape of the overall sprite:
For a good visualization of collision shapes and the mathematics behind the collision detection, visit Jeffrey Thompson’s Collision Detection Page
Thus, circular sprites are represented by circles, and rectangular sprites by rectangles. Very small sprites (like circles) can be approximated by a point. Circles, rectangles, and points are by far the most common of 2D collision shapes, because the mathematics involved in detecting collisions with these shapes is very straightforward, and because the memory required to store these collision shapes is minimal.
Bounding points are typically defined with a single point (x & y). Bounding circles are typically defined with a center point (x & y) and a radius. Bounding rectangles are typically defined by a position (x & y) and a width and height - although an alternate definition using left, top, right, and bottom values is also sometimes used. Also, while the position often refers to the upper left corner, it can also be set in the center of the rectangle, or at the middle bottom, or anywhere else that is convenient - as long as the positioning is consistent throughout the game code, it won’t be an issue.
These values can be stored as either an integer or floating point number. When rendered on-screen, any fractional values will be converted to whole pixels, but using floats can preserve more detail until that point.
Here are some straightforward struct representations for each:
public struct BoundingCircle
{
public float X;
public float Y;
public float Radius;
}
public struct BoundingRectangle
{
public float X;
public float Y;
public float Width;
public float Height;
}
public struct BoundingPoint
{
public float X;
public float Y;
}Point on Point Collisions
Because a point has no size, two points collide only if they have the same x and y values. In other words, two points collide if they are the same point. This is simple to implement in code:
/// <summary>
/// Detects a collision between two points
/// </summary>
/// <param name="p1">the first point</param>
/// <param name="p2">the second point</param>
/// <returns>true when colliding, false otherwise</returns>
public static bool Collides(BoundingPoint p1, BoundingPoint p2)
{
return p1.X == p2.X && p1.Y == p2.Y;
}Circle on Circle Collisions
Only slightly harder than checking for collisions between two points is a collision between two circles. Remember a circle is defined as all points that are $ radius $ distance from the $ center $. For two circles to collide, some of these points must fall within the region defined by the other. If we were to draw a line from center to center:
We can very quickly see that if the length of this line is greater than the sum of the radii of the circle, the two circles do not overlap. We can calculate the distance between the circles using the distance formula:
$$ distance = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$This can then be compared to the sum of the two circle’s radii, giving us an indication of the relationship between the two shapes:
$$ \displaylines{ (r_2 + r_1) < \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \quad \text{The circles do not intersect} \\ (r_2 + r_1) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \quad \text{The circles touch} \\ (r_2 + r_1) > \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \quad \text{The circles overlap} \\ } $$However, computing the square root is a costly operation in computational terms, so we will typically square both sides of the equation and use a comparison of the squares instead:
$$ \displaylines{ (r_2 + r_1)^2 < (x_2 - x_1)^2 + (y_2 - y_1)^2 \quad \text{The circles do not intersect} \\ (r_2 + r_1)^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2 \quad \text{The circles touch} \\ (r_2 + r_1)^2 > (x_2 - x_1)^2 + (y_2 - y_1)^2 \quad \text{The circles overlap} \\ } $$From these inequalities we can very easily write a test for determining if our shapes collide.
/// <summary>
/// Detects a collision between two circles
/// </summary>
/// <param name="c1">the first circle</param>
/// <param name="c2">the second circle</param>
/// <returns>true for a collision, false otherwise</returns>
public static bool Collides(BoundingCircle c1, BoundingCircle c2)
{
return Math.Pow(c1.Radius + c2.Radius, 2) >= Math.Pow(c2.X - c1.X, 2) + Math.Pow(c2.Y - c1.Y, 2);
}Rectangle on Rectangle Collisions
There are many possible algorithms to use in detecting when a rectangle collides with another rectangle, each with its own strengths and weaknesses. Again, we can turn to a graphical representation to help us generate our test:
From this first image, we might assume that two rectangles collide if one of their corners falls within the other. Thus, we might think that simply checking if any of the corners of one rectangle fall within the other would give us our result. But that overlooks one important case:
As this example makes clear, the important concept is that one rectangle must overlap the other rectangle in two dimensions (both the X and the Y) for a collision to occur. Thus, we could check:
Horizontally:
- if a’s left side falls within b’s horizontal span
- or if a’s right side falls within b’s horizontal span
- or if b’s left side falls within a’s horizontal span
- or if b’s right side falls within a’s horizontal span
and vertically:
- if a’s top side falls within b’s vertical span
- or if a’s bottom side falls within b’s vertical span
- or if b’s top side falls within a’s vertical span
- or if b’s bottom side falls within a’s vertical span
That is a lot of cases! It also makes for a monster boolean expression, an does a lot of operations. As with many boolean expressions, we can instead consider the negation - proving that the two rectangles do not overlap. This is far simpler; all we need to prove is that the two do not overlap horizontally or vertically. Thus we can check:
Horizontally:
- if a is to the left of b
- or if a is to the right of b
or Vertically:
- if a is above b
- or if a is below b
/// <summary>
/// Detects a collision between two rectangles
/// </summary>
/// <param name="r1">The first rectangle</param>
/// <param name="r2">The second rectangle</param>
/// <returns>true on collision, false otherwise</returns>
public static bool Collides(BoundingRectangle r1, BoundingRectangle r2)
{
return !(r1.X + r1.Width < r2.X // r1 is to the left of r2
|| r1.X > r2.X + r2.Width // r1 is to the right of r2
|| r1.Y + r1.Height < r2.Y // r1 is above r2
|| r1.Y > r2.Y + r2.Height); // r1 is below r2
}Point on Circle Collisions
To determine if a point and circle collide is a degenerate case of circle on circle collision where one circle has a radius of 0. Thus:
$$ r >= \sqrt{(x_c - x_p)^2 + (y_c - y_p)^2} \quad \text{collision} $$Which can be rewritten to avoid the square root as:
$$ r^2 >= (x_c - x_p)^2 + (y_c - y_p)^2 \quad \text{collision} $$And in code:
/// <summary>
/// Detects a collision between a circle and point
/// </summary>
/// <param name="c">the circle</param>
/// <param name="p">the point</param>
/// <returns>true on collision, false otherwise</returns>
public static bool Collides(BoundingCircle c, BoundingPoint p)
{
return Math.Pow(c.Radius, 2) >= Math.Pow(c.X - p.X, 2) + Math.Pow(c.Y - p.Y, 2);
}Point on Rectangle Collisions
Similarly, a point and rectangle collide if the point falls within the bounds or on an edge of the rectangle.
/// <summary>
/// Detects a collision between a rectangle and a point
/// </summary>
/// <param name="r">The rectangle</param>
/// <param name="p">The point</param>
/// <returns>true on collision, false otherwise</returns>
public static bool Collides(BoundingRectangle r, BoundingPoint p)
{
return p.X >= r.X && p.X <= r.X + r.Width && p.Y >= r.Y && p.Y <= r.Y + r.Height;
}Circle on Rectangle Collisions
A circle-on-rectangle collision is a bit more challenging. To understand our strategy, let’s start with a number line:
Notice the red line from 0 to 4? What is the closest point that falls within that line to the value -2? To the value 5? To the value 3? The answers are: 0, 3, and 4. Basically, if the point falls within the section, it is the point itself. Otherwise it is the closest endpoint. Mathematically, this is the clamp operation, and MonoGame provides a method to calculate it: MathHelper.Clamp(float value, float min, float max). It will clamp the provided value to the provided min and max.
If we clamp the circle’s center point to the extents of the rectangle, the result is the nearest point in or on the rectangle to the center of the circle. If the distance between the center and the nearest point is greater than the radius of the circle, then we know the two aren’t intersecting. We can write this using the point/circle test we declared earlier:
/// <summary>
/// Determines if there is a collision between a circle and rectangle
/// </summary>
/// <param name="r">The bounding rectangle</param>
/// <param name="c">The bounding circle</param>
/// <returns>true for collision, false otherwise</returns>
public static bool Collides(BoundingRectangle r, BoundingCircle c)
{
BoundingPoint p;
p.X = MathHelper.Clamp(c.X, r.X, r.X + r.Width);
p.Y = MathHelper.Clamp(c.Y, r.Y, r.Y + r.Height);
return Collides(c, p);
}