Subsections of Conditionals
Introduction
YouTube VideoResources
In this lab, we’re going to introduce another data type in Python, the Boolean data type. Working with Boolean values in programming is a very important skill to learn.
Elsewhere in this course, we’ve already learned about Boolean values and how they work, so we won’t cover that information again here. Feel free to refer to other areas in this course for more background on Booleans, Boolean Logic, Boolean Algebra, and other related topics.
In this lab, we’ll learn how to create Boolean values in Python, as well as the various Boolean operators and comparators that can we can use in our code. Then, we’ll explore how to use conditional statements to affect the control flow of our programs. This allows us to build programs that will perform different tasks based on the input we receive from the user, which is a very key concept in programming. Let’s get to it!
Subsections of Introduction
Booleans
YouTube VideoResources
In Python, Boolean values are stored in the bool data type. Variables of the bool data type can only store one of two values, True or False. So, a Boolean value is really the simplest data value we can imagine - it is a single binary bit representing a value of True or False.
To create a Boolean variable in Python, we can simply assign those values to a variable in an assignment statement:
a = True
b = False
print(a)
print(type(b))When we execute that code, we’ll see the following output:
True
<class 'bool'>In Python, we use the keywords True and False to represent Boolean values. In Python, it is very important to make sure these values are capitalized, otherwise the program will not work properly. Also, since these are keywords and not strings, we don’t need to put them in quotation marks.
Converting Between Data Types
Python includes the special bool() function, which can be used to convert any data type into a Boolean value. The bool() function follows these rules to determine what to return:
- If the input is the value
False, the value0, the valueNone, or anything with 0 length, including the empty string, it will returnFalse. - Otherwise, for all other values it will return
True.
Let’s look at a couple of quick examples. First, let’s try to convert the strings "True" and "False" to their Boolean equivalents:
print(bool("True"))
print(bool("False"))When this code is executed, we’ll see this output:
True
TrueThis seems a bit strange, since the string "False" ended up creating the Boolean value True. However, if we look at the rules above, since the string "False" has a length greater than 1, and it is not any of the special values listed above, it should always result in the Boolean value True.
In this example, we can check a couple of special values using the bool() function:
print(bool(0))
print(bool(1))
print(bool(""))In this case, we’ll see the following output:
False
True
FalseHere, we see that the value 0, as well as the empty string "", both result in a value of False. However, the value 1 is True, since it is a non-zero value.
In practice, we won’t use the bool() function directly very often. Instead, if we want to determine if a user inputs a True or False value, we can just use one of the Boolean comparators that we’ll see later in this lab.
Subsections of Booleans
Boolean Operators
YouTube VideoResources
Python also includes several operators that can be applied to one or two Boolean values. These operators make up the basis of Boolean logic, and allow us to construct complex expressions of Boolean values. Let’s quickly review the three basic Boolean operators present in Python.
And Operator
In Python, we use the keyword and to perform the Boolean and operation. This operator will return True if both input values are also True, otherwise it will return False.
This corresponds to the following truth table:
| Variable 1 | Variable 2 | Result |
|---|---|---|
| F | F | F |
| F | T | F |
| T | F | F |
| T | T | T |
Here’s a quick example of the and operator in Python:
x = True
y = False
print(x and y)When we run this Python code, we should see this output:
FalseSince the variable y is False, the resulting value is also False.
Or Operator
Likewise, the keyword or is used in Python for the Boolean or operation. This operator will return True if either of the input values is True, but it will return False if neither of them are True.
This corresponds to the following truth table:
| Variable 1 | Variable 2 | Result |
|---|---|---|
| F | F | F |
| F | T | T |
| T | F | T |
| T | T | T |
Let’s look at an example:
a = False
b = True
print(a or b)When we execute this code, we’ll get this output:
TrueSince b is True, we know that at least one input is True and the result of a or b is also True.
Not Operator
Finally, Python uses the keyword not to represent the Boolean not operation, which simply inverts a Boolean value from True to False and vice-versa.
This corresponds to the following truth table:
| Variable 1 | Result |
|---|---|
| F | T |
| T | F |
Here’s an example:
x = True
print(not x)
print(not not x)When we run this code, we’ll see this printed to the terminal:
False
TrueSince x is True, we know that not x is False. We can then perform the not operation again, on that result, as shown in not not x, which will result in the original value of x, which is True.
Subsections of Boolean Operators
Boolean Comparators
YouTube VideoResources
Python also uses various comparators to allow us to compare values of many different data types to produce a Boolean value. We can compare numbers, strings, and many other data types in Python using these comparators.
The basic comparators in Python are:
==equal!=not equal<less than<=less than or equal to>greater than>=greater than or equal to
Notice that the equal comparator in Python now uses two equals signs == instead of a single one. This is because the single equals sign = is used in the assignment statement, and we don’t want to confuse a Boolean comparator for an assignment. So, in Python, as in most other programming languages, we use two equals signs == when comparing values, and one equals sign = when we are storing a value in a variable.
Comparing values
We usually only want to compare values of the same data type using comparators. It really only makes sense to compare strings to strings, and Booleans to Booleans. However, for the numeric data types int and float, we can easily compare values of either data type together in Python.
Consider the following example:
x = 5
y = 5.0
print(x == y)When we execute this code, we’ll get this output:
TrueEven though x is the int data type and y is the float data type, they both store the same numerical value, and our comparators will work just like we expect. So, we can easily compare both integers and floating-point values in our code.
Behind the scenes, when we compare an int and a float value in Python, Python will convert the values to a common data type, usually the float data type, using the appropriate conversion function. This is known as coercion in programming - the program is essentially forcing a value of one data type into another data type because of an operation. However, it won’t change the data type of the variable involved, just the value it is evaluating.
Strings in Python can also be compared using the various comparator operators. When two strings are compared using any type of “less than” or “greater than” comparator, they will be compared according to their lexicographic order. In general, this means that each letter will be ordered based on its value in the ASCII encoding standard.
Let’s look at a quick example:
a = "First"
b = "fir"
print(a < b)When we run this code, we’ll see this output:
TrueThis may seem surprising, since we’d expect the word "fir" to come before the word "First" in a dictionary, since it has fewer letters. However, in Python, the letters "f" and "F" are not treated identically. According to the ASCII encoding standard, capital letters have a lower value than lower-case letters, so all words starting with a capital "F" will come before any words starting with a lower-case "f".
This can be a bit confusing, so it is always important to remember that we can always write a quick sample program in Python to test how a particular operator will work for a given set of values. If nothing else, we can always count on our computer to produce the same result for the same operation, no matter if it is part of a larger program or a small test program.
Order of Operations
Finally, Python’s order of operations can be updated to include these Boolean comparators and operators. So, when we see an expression that combines mathematical operators with Boolean operators and comparators, we’ll follow this order:
- Math operators (according to their order of operations)
- Boolean comparators
notoperatorandoperatororoperator
As always, it is considered good practice to include parentheses in any complex expressions to make sure that the intent is clear, regardless of the order of operations.
Subsections of Boolean Comparators
Boolean Practice
Let’s try some simple practice problems. These problems are not graded - they are just for you to practice before doing the real exercises in the lab itself. You can find the answers below each question by clicking the button below each question.
4.1 Reading Code
What is printed to the terminal when the following Python program is run?
a = 5
b = 10
c = 15
x = b > a and c < b or (not (a + b > c))
y = b + a >= c or c / a > b / a
z = c - b != a and not c % a == 0
print(x)
print(y)
print(z)Try to work out the solution yourself first before running the code.
4.2 Reading Code
What is printed to the terminal when the following Python program is run?
x = 7
y = 42
z = 6
a = x >= z and y <= x * z or not y % z == 0
b = not (y // x <= z or x - z > 0 or y % x != 1)
c = y // (z + x) < z / 2 and not bool(z)
print(a)
print(b)
print(c)Try to work out the solution yourself first before running the code.
4.3 Writing Code
Write a Python program that performs the following operations:
- Prompts the user for four integer inputs and stores them in variables
- If the first input is strictly smaller than all other inputs, and the last input is strictly larger than all other inputs, print
True. If not, printFalse.
Your program may not use any conditional statements (if statements).
Hint: what comparisons must be made, and what comparisons do not need to be made, to answer these questions definitively?
4.4 Writing Code
Write a complete program in Python that performs the following operations:
- Prompts the user for three integer inputs and stores them in variables.
- If the second and third inputs are multiples of the first, and the third input is a multiple of the second, print
true. If not, printfalse.
Your program may not use any conditional statements (if statements).
Hint: you can use the modulo % operator to determine if one number is evenly divisible by another number. Can this also tell you which number is a multiple of another number?
If
YouTube VideoResources
Now that we understand how to use Boolean values in our programs, it’s time to put those values to use. One way to think of the result of a Boolean expression is that it helps us make a decision in our programs. For example, if we want to do something special in our program when the user inputs the value
$ 42 $ into the variable x, then we can write the Boolean expression x == 42 to help us decide if the user input the correct value.
Once we have that decision made, we need some way to tell our program to run a different piece of code based on the outcome of that decision. In Python, as well as most other programming languages, we can use a special construct called an if statement to do this. If statements are one example of a conditional statement in programming.
These conditional statements allow us to affect the control flow of our programs. Effectively, we can use a Boolean expression to determine whether a particular piece of code should be executed or not. In an if statement, we include a Boolean expression and a block of statements. If the Boolean expression evaluates to True, then we execute the code in the block of statements. If it is False, then we skip the block and continue with the rest of the program.
The structure of an if statement in Python is shown below:
if <boolean expression>:
<block of statements>In this structure, we have a <boolean expression> that is evaluated. After the Boolean expression is a colon :.
Then, the <block of statements> is included below the if statement’s first line, and it must be indented one level. In Python, the <block of statements> must include at least one line of code, otherwise Python won’t be able to understand it.
Indentation in Python
Let’s briefly discuss indentation in Python, since it is very important and is usually something that trips up new Python developers. Most programming languages use symbols such as curly braces {} to surround blocks of statements in code, making it easy to tell where one block ends and another begins. Similarly, those languages also use symbols such as semicolons ; at the end of each line of code, indicating the end of a particular statement.
These programming languages use those symbols to make it clear to both the developer and the computer where a particular line or block of code begins and ends, and it makes it very easy for tools to understand and run the code. As an interesting side effect, it also means that the code doesn’t need to follow any particular structure beyond the use of those symbols - many of the languages allow developers to place multiple statements, or even entire programs, on a single line of code. Likewise, indentation is completely optional, and only done to help make the code more readable.
Python takes a different approach. Instead of using symbols like semicolons ; and curly braces {} to show the structure of the code, Python uses newlines and indentation for this purpose. By doing so, Python is simultaneously simpler (since it has fewer symbols to learn) and more complex (the indentation has meaning) than other languages. It’s really a tradeoff, though most Python programmers will admit that not having to deal with special symbols in Python is well worth the effort of making sure that the indentation is correct, especially since most other languages follow the same conventions anyway, even if it isn’t strictly required.
So, how can we indent code in Python? Typically, we use four consecutive spaces for each level of indentation. So, below the conditional statement if <boolean expression>: shown above, we would place four spaces before the first line of the <block of statements>, and then continue to do so for each line below that should be included in the block of code.
Thankfully, most text editors used for programming, such as Codio, Atom, Visual Studio Code, and more, are all configured to convert tabs to spaces. So, we can simply press the Tab key on the keyboard to insert the correct amount of spaces for one level of indentation. Likewise, we can usually use Shift+Tab to remove four spaces.
Finally, it is worth noting that there is a special symbol that actually is a tab in text, which is represented as \t in a string. Like the newline symbol, we can’t see it in our UI in most cases, but it is there. Some non-programming text editors, such as Notepad in Windows, will insert that symbol instead of four spaces when we press the Tab key. If we try to run a program that contains those symbols, the Python interpreter may not be able to read our program and will give us an error about inconsistent use of tabs and spaces. If that happens, we’ll need to make sure our program is consistently using only tabs or spaces for indentation. Most editors used for programming have a special function for converting tabs to spaces, and there are lots of online tools available for this as well.
Code Tracing Example - False
Let’s go through a couple of code tracing examples in Python Tutor to see how an if statement works in code.
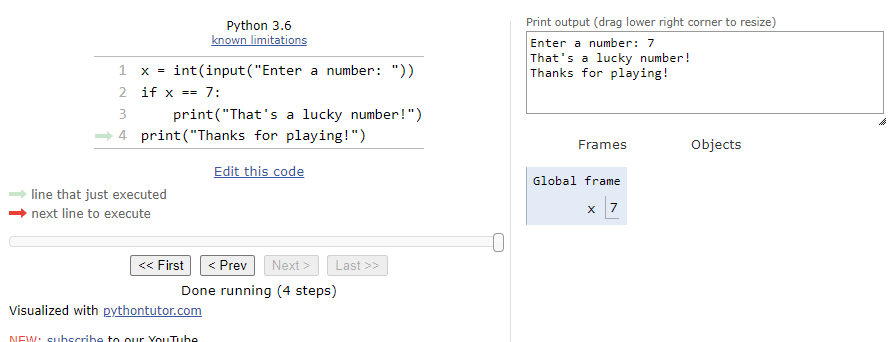
Consider this program in Python:
x = int(input("Enter a number: "))
if x == 7:
print("That's a lucky number!")
print("Thanks for playing!")We can see this example by clicking on this Python Tutor link. At first, our window should look something like this:
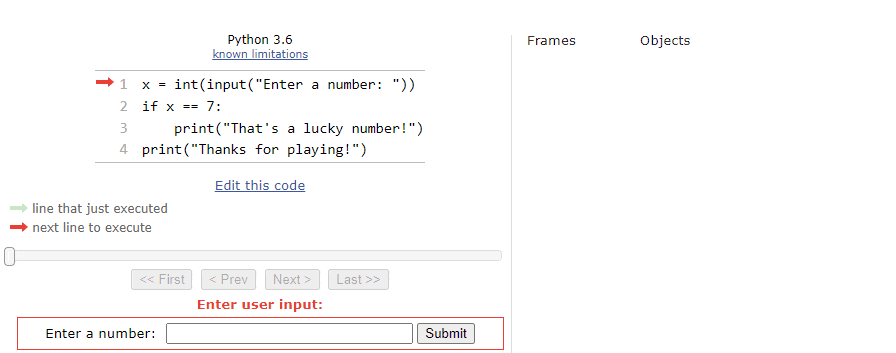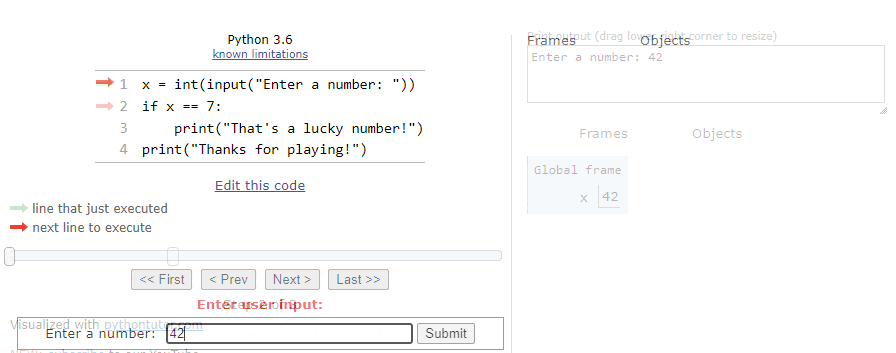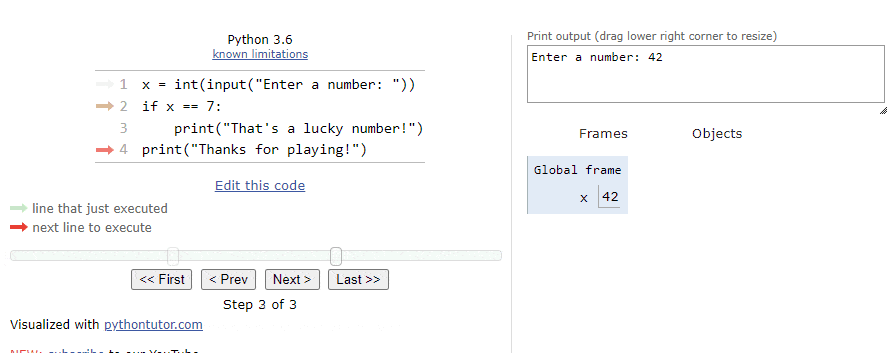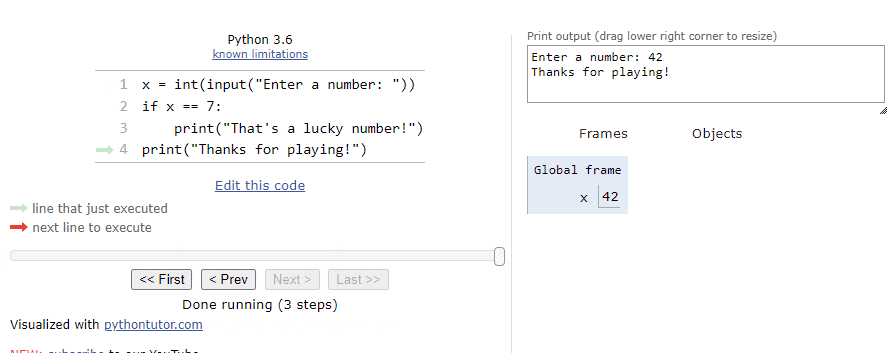
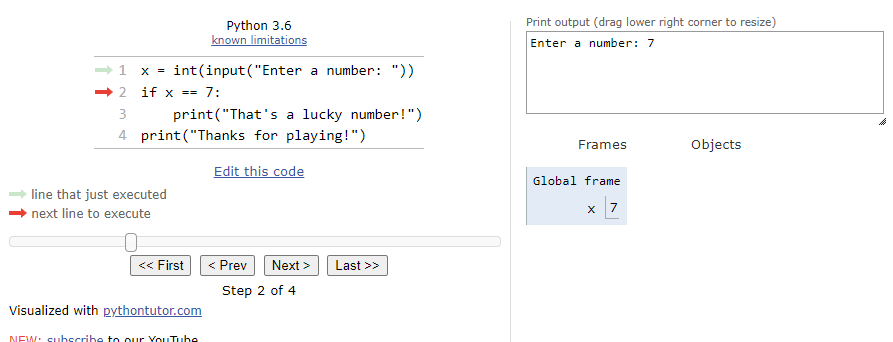
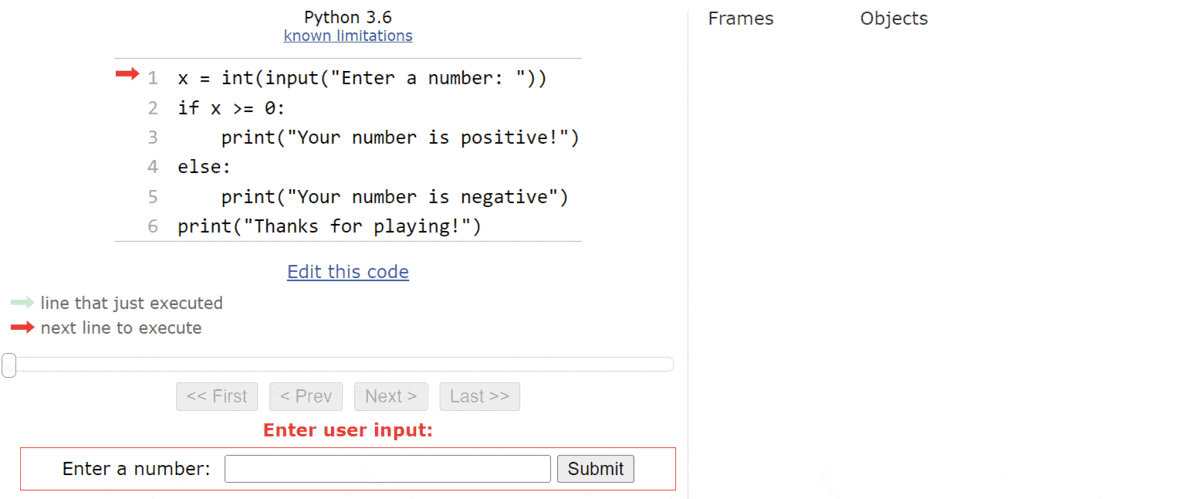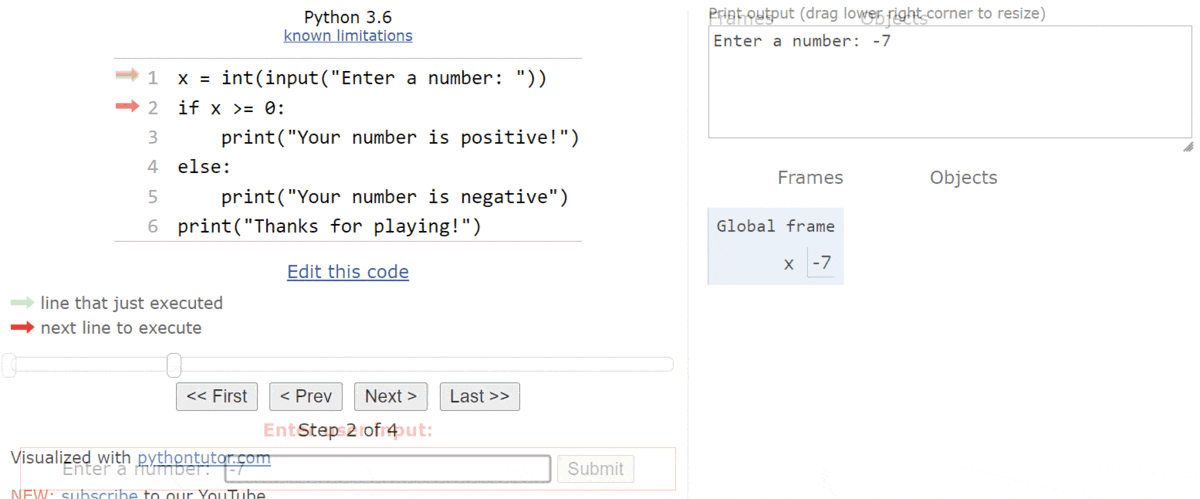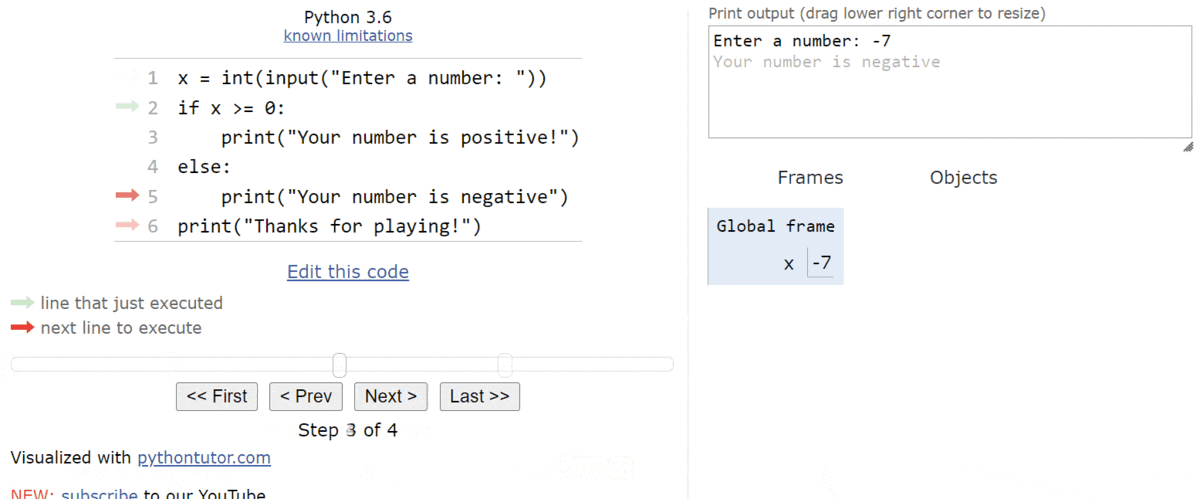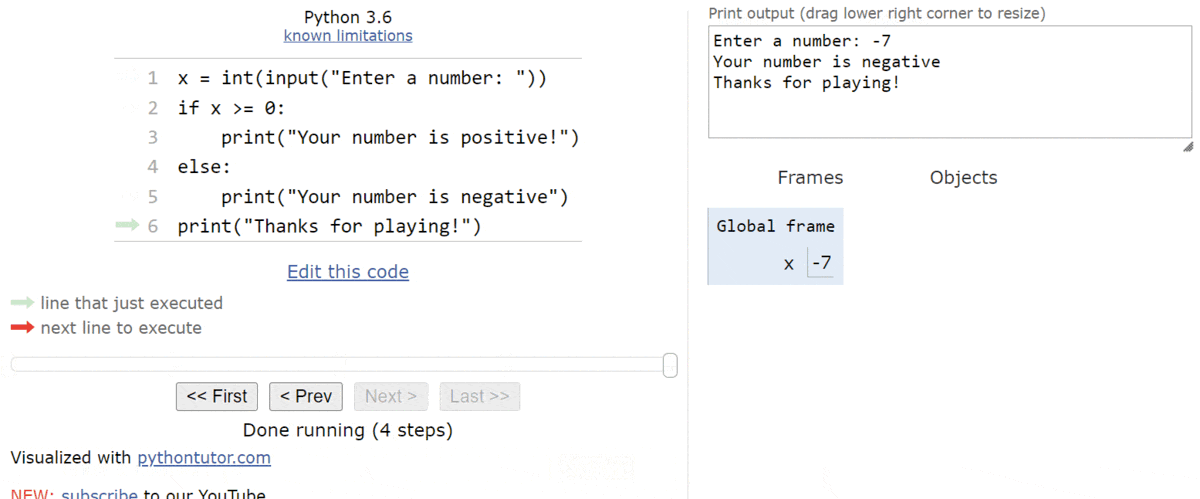
When we step through the program, the first line of code will ask the user to input a number, so Python Tutor will show an input box at the bottom of the window:
For this first time through the program, let’s assume the user inputs the string "42" as input:
So, when we click Submit, we’ll see the integer value
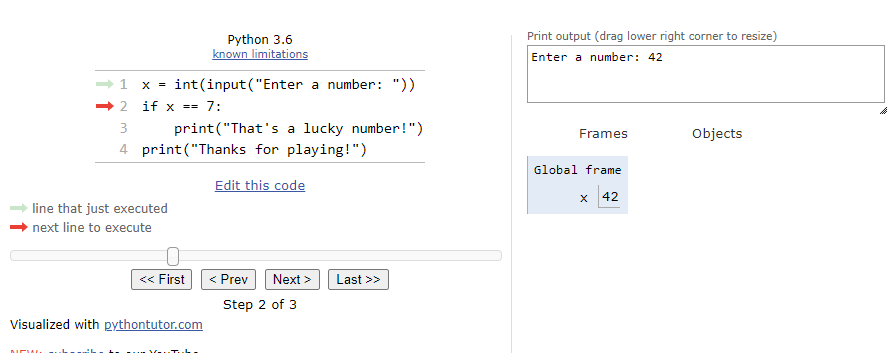
$ 42 $ stored in the variable x in the Global frame:
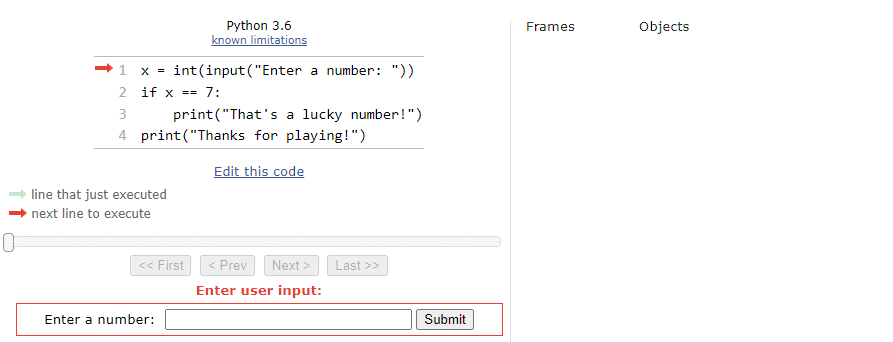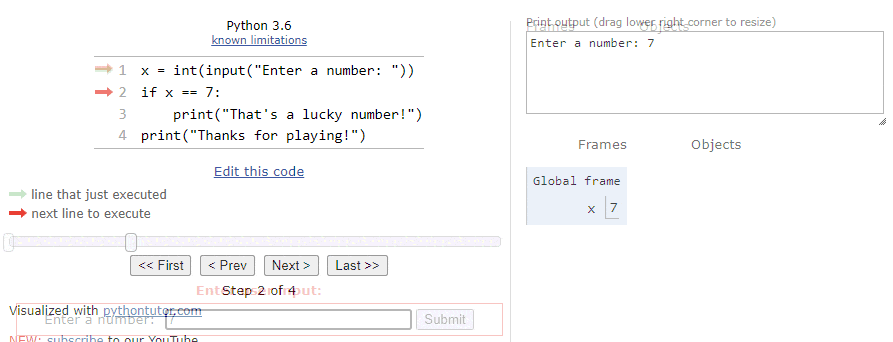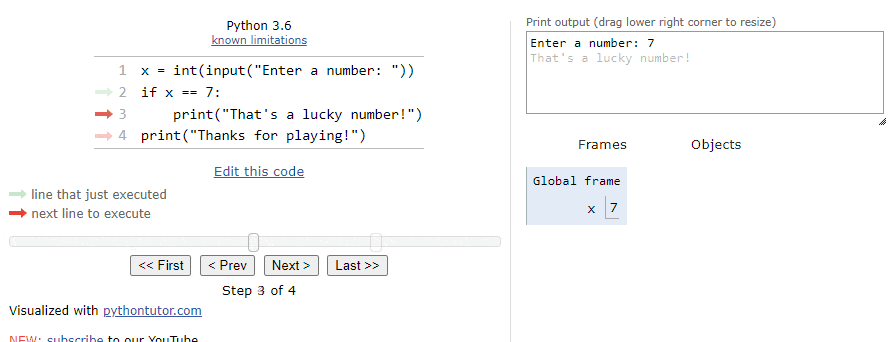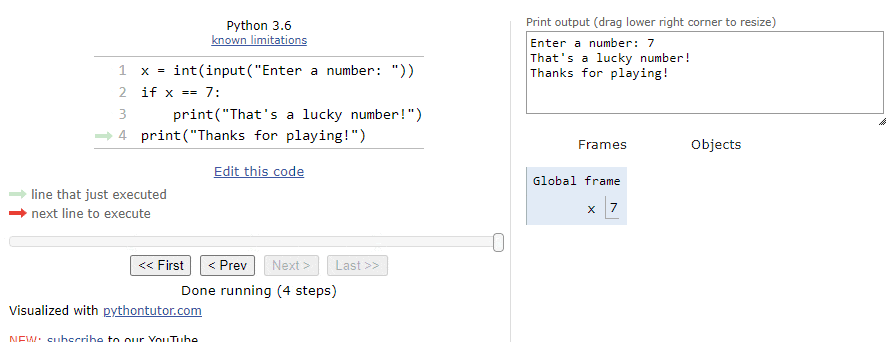
At this point, we’ve reached the if statement. The first step is to evaluate the Boolean expression x == 7. Since x is actually storing the value
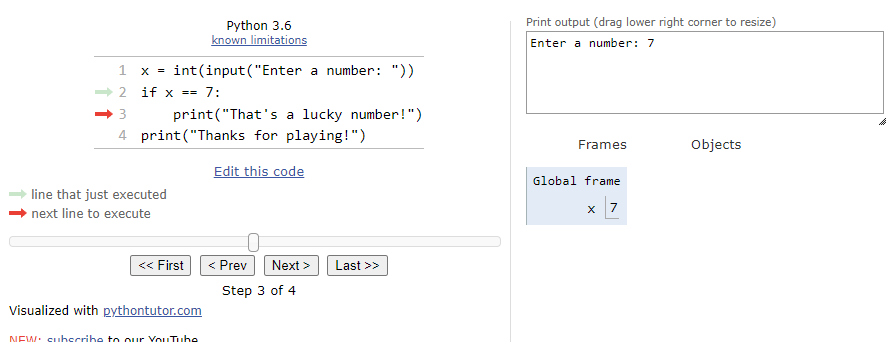
$ 42 $, this statement will evaluate to False. So, when we click the Next button on the state below:
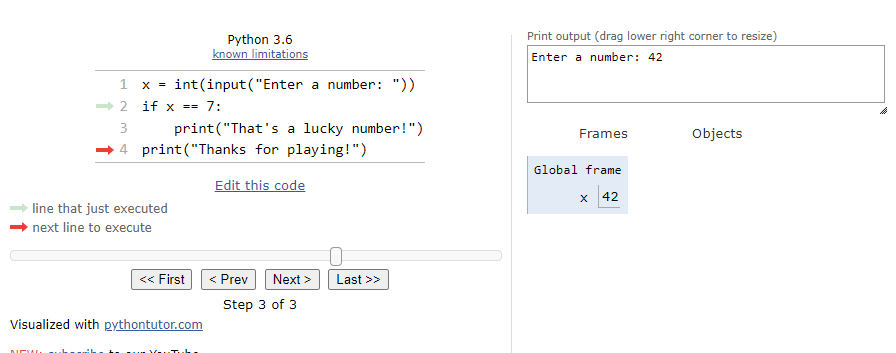
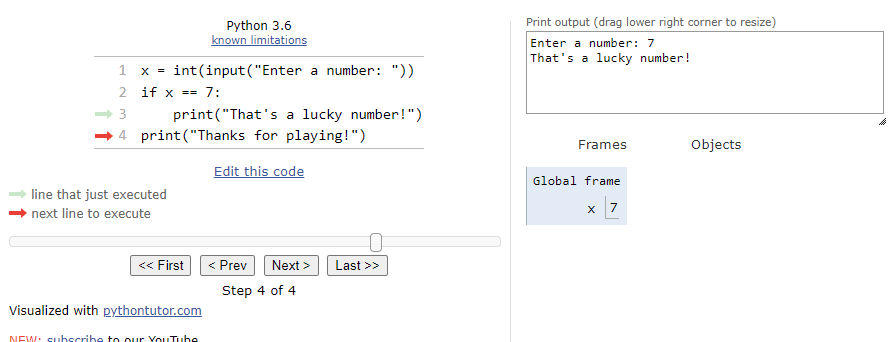
We’ll see that the program arrow jumps past the block of statements in the if statement. So, the next line will simply print the goodbye message:
The entire process is shown in the animation below:
As we can see, when the Boolean expression evaluates to False, we’ll just skip the block of statements inside of the if statement.
Code Tracing Example - True
Now let’s see what happens when the Boolean expression evaluates to True instead. To see that, we can go back to the point where our program is asking for input, as shown below:
This time, we’ll assume the user inputs the string "7" as input.
So, when we click Submit, we’ll see the integer value
$ 7 $ stored in the variable x in the Global frame:
This time, when we reach the if statement, we’ll see that the Boolean expression x == 7 will evaluate to True. So, when we click the Next button, we’ll be taken to the block of statements inside of the if statement:
Here, we’ll print the special message for finding a lucky number:
Then, we’ll print the program’s goodbye message:
The entire process can be seen in this animation:
So, when the Boolean expression evaluates to True, we’ll run the code inside the if statement. If it is False, then we’ll just skip past the if statement and continue with the rest of our program.
If Statement Flowchart
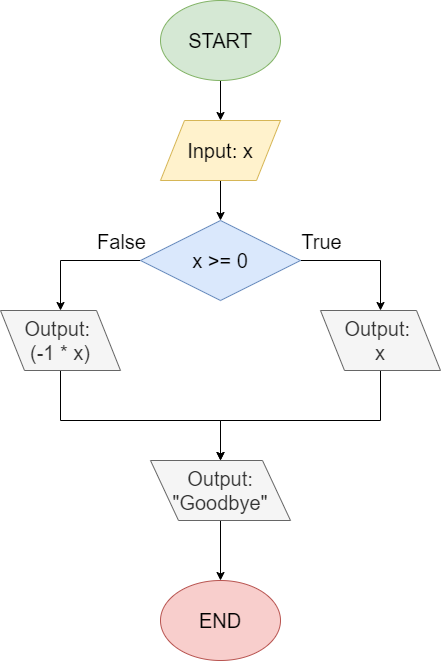
Another way to visualize an if statement is using a flowchart. Consider the following Python code:
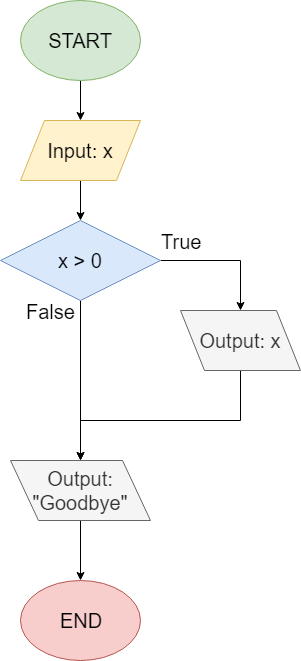
x = int(input("Input: "))
if x > 0:
print(x)
print("Goodbye")This Python code can also be represented as the flowchart shown below:
When we read flowcharts like this, we typically go from top to bottom, starting with the circle labeled “START”. The first step is to read input from the user, and store that value in the variable x.
Then, we reach a decision node, which uses a diamond shape. This node asks if the value in the variable x is greater than 0. Notice that there are two lines coming from the decision node: one labeled “True” and another labeled “False”. They correspond to the possible values that can result from evaluating the Boolean expression x > 0. So, if the result of that expression is True, then we’ll follow the path that exits the diamond from the side labeled “True”, and we’ll output the value x to the terminal. Once that is done, we can follow that path around to the next box that will output the string "Goodbye".
If that result is False, then we’ll follow the downward path labeled “False” and skip the path to the side. Instead, we’ll just reach the line that prints "Goodbye" and then end the program.
As we learn how to use if statements in our code, we might find it easier to use flowcharts or other tools to help understand exactly what our program will do. The path that a program takes through a flowchart like this is called the control flow of the program. We’ll discuss that topic a bit more toward the end of this lab.
Subsections of If
If-Else
YouTube VideoResources
Python also supports another kind of conditional statement, the if-else statement. An if-else statement contains a single Boolean expression, but two blocks of code. If the Boolean expression evaluates to True, then one block of statements is executed. If it is False, then the other block will be executed.
The general structure of an if-else statement in Python is shown below:
if <boolean expression>:
<block of statements 1>
else:
<block of statements 2>Notice that the else keyword is followed by a colon, just like the first line of the if-else statement. As we’d expect, the first block of statements is executed if the <boolean expression> portion is True and the second block is executed if it is False.
Once again, let’s go through a couple of code traces using Python Tutor to explore how an if-else statement works in Python.
Code Tracing Example - True
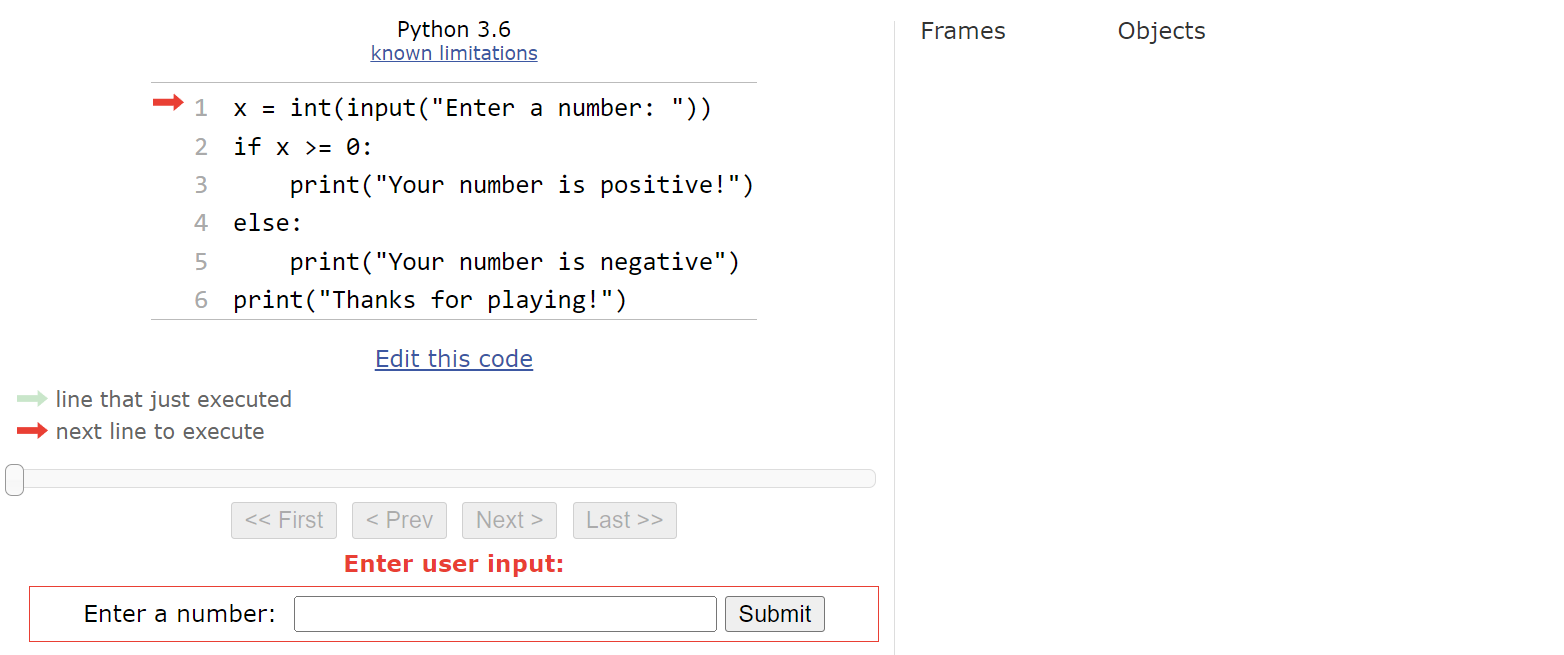
Here’s a simple Python program that contains an if-else statement:
x = int(input("Enter a number: "))
if x >= 0:
print("Your number is positive!")
else:
print("Your number is negative")
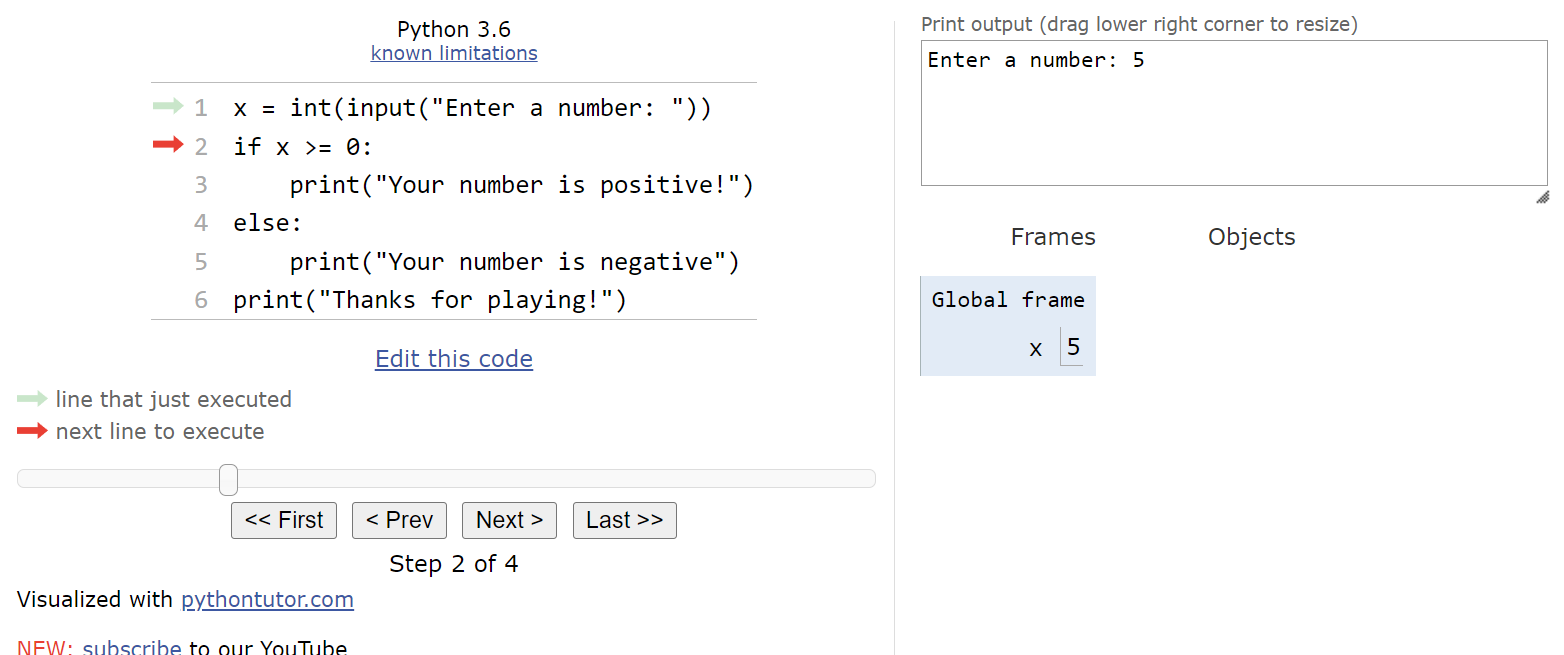
print("Thanks for playing!")This program accepts an input from the user, converts it to an integer, and then determines if the integer is a positive or negative number. Let’s go through this program a couple of times in Python Tutor to see how it works. As always, you can copy and paste this code into Python Tutor, or click this Python Tutor link to follow along!
We’ll start an input prompt as shown here:
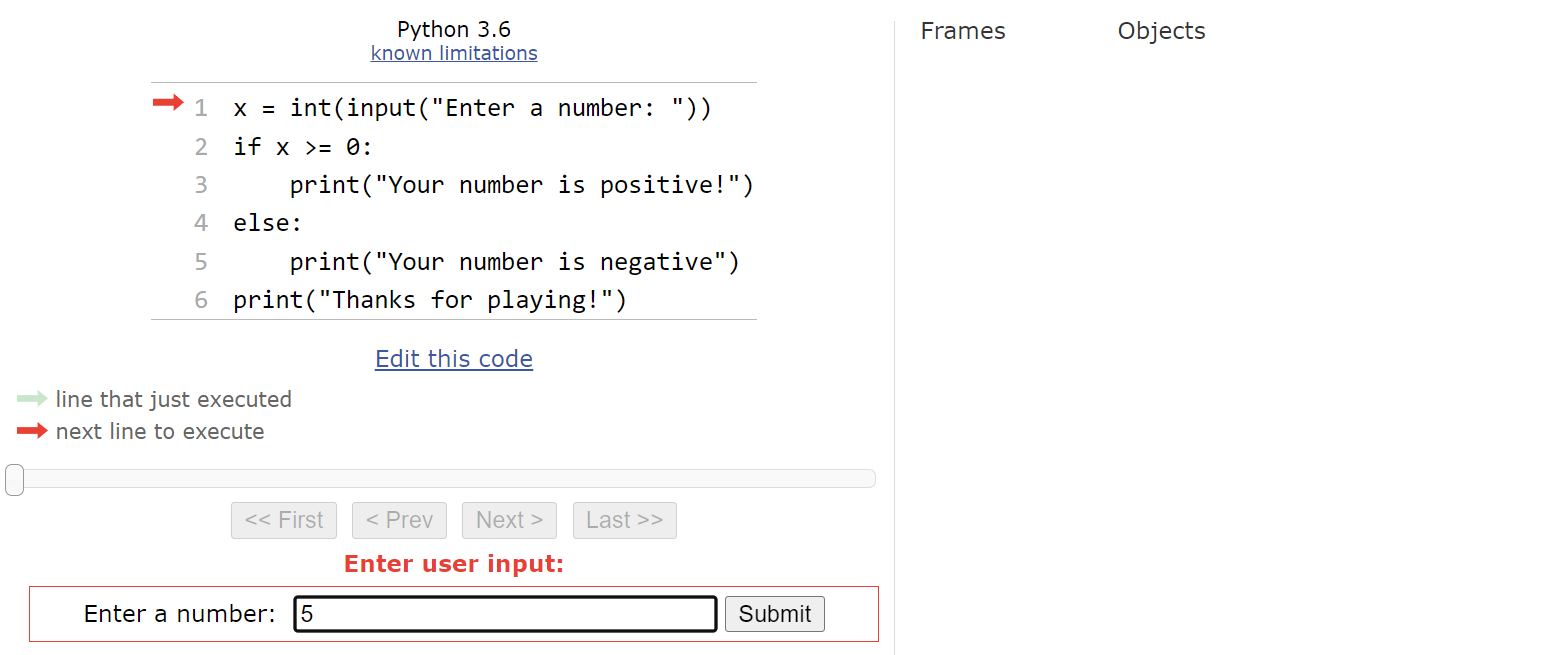
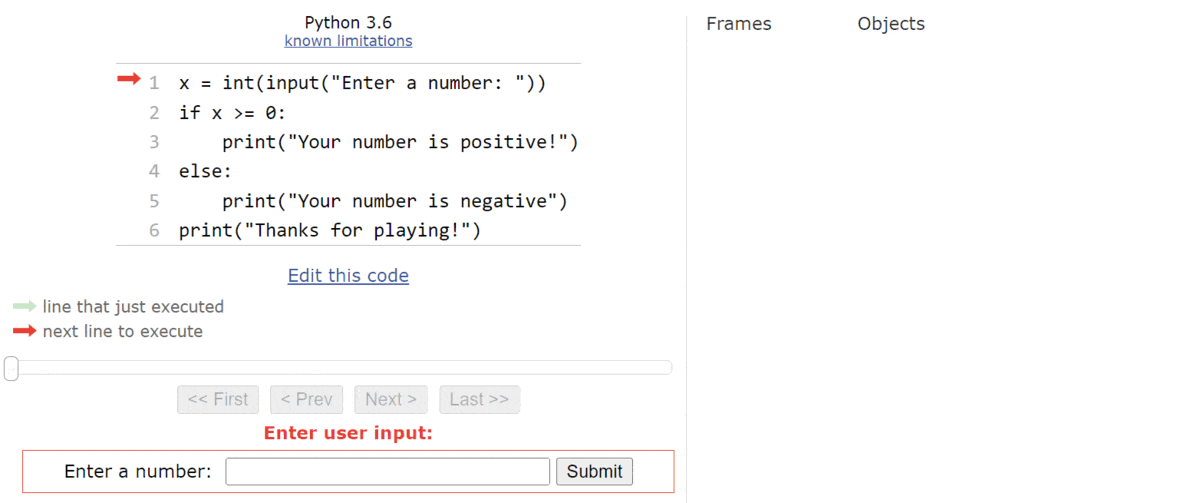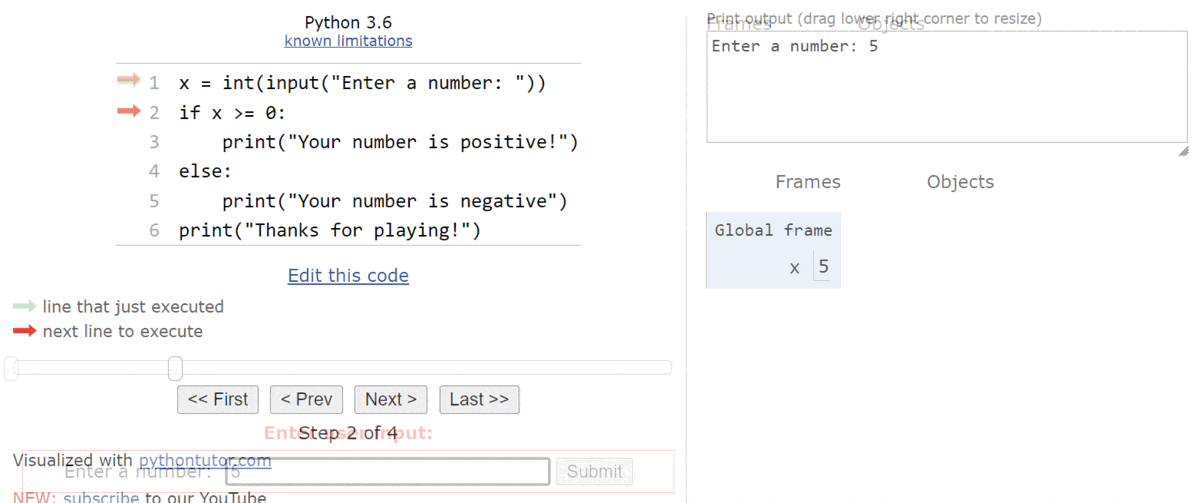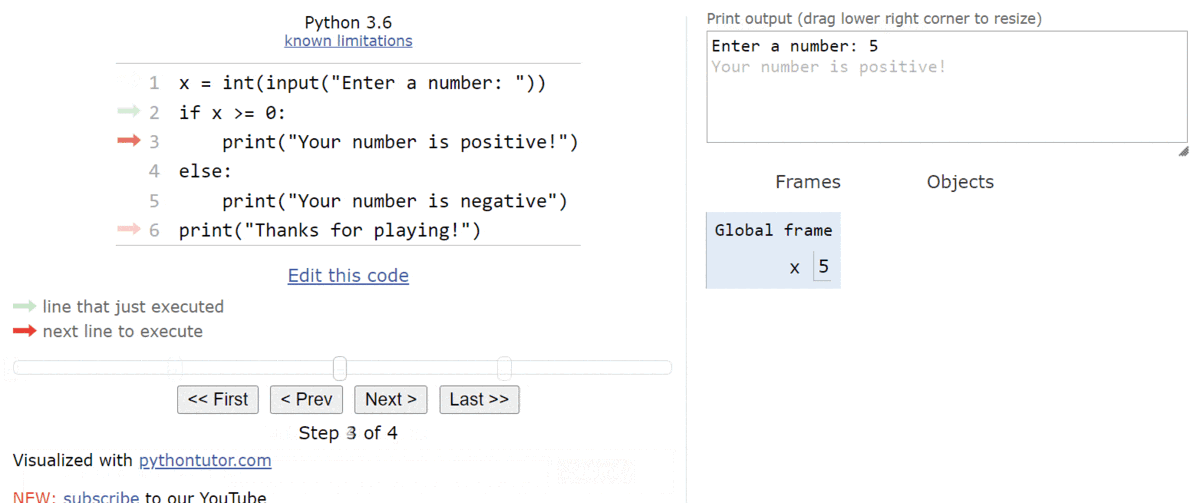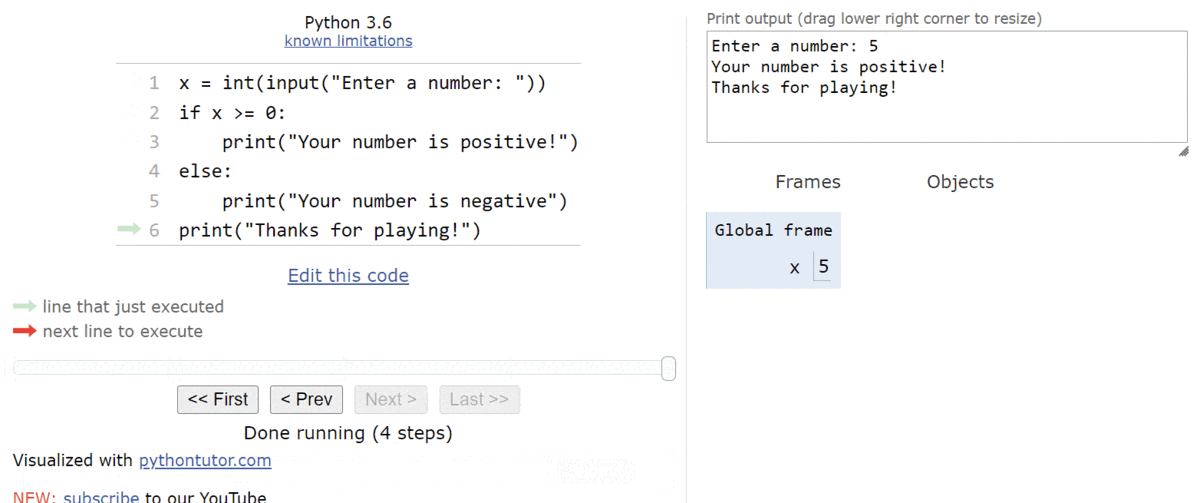
Let’s assume that the user inputs the string "5" here.
That means that the integer value
$ 5 $ will be stored in the variable named x:
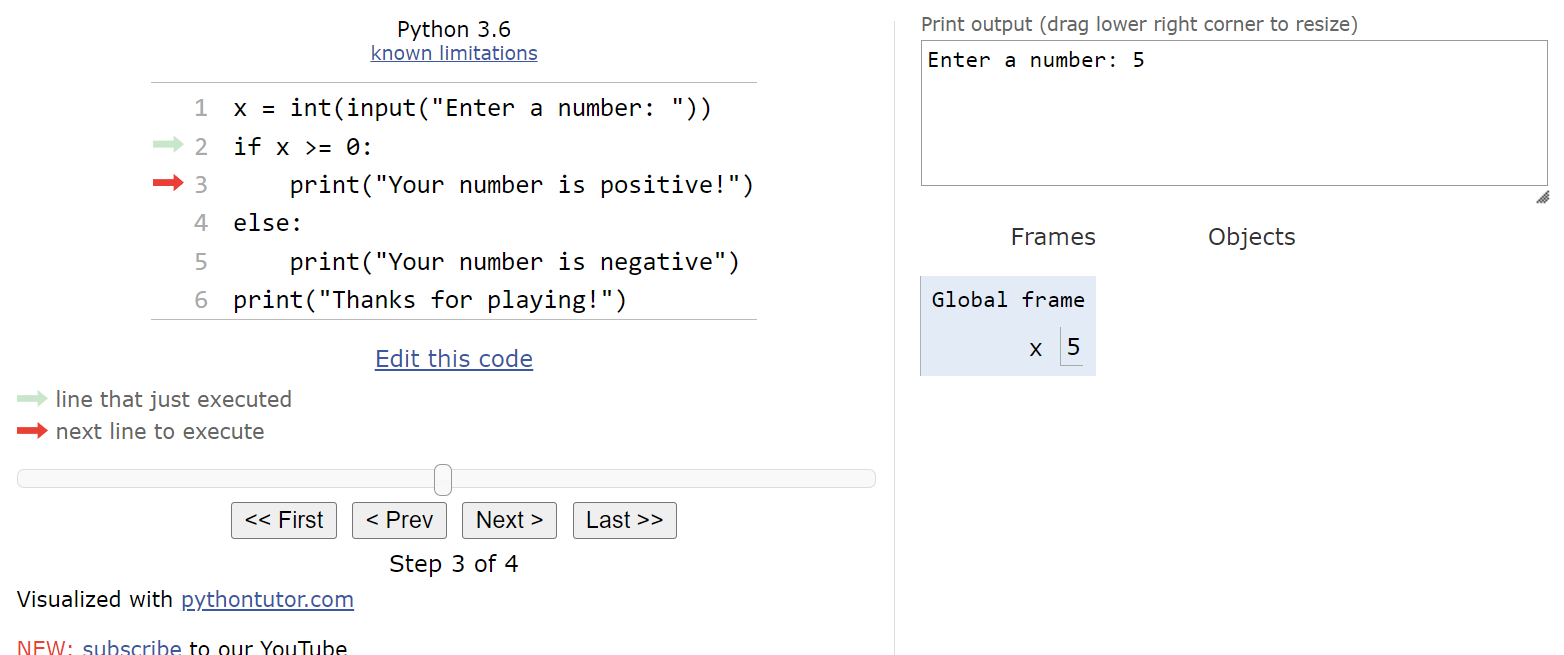
Now we’ve reached the if-else statement. So, we’ll need to evaluate the Boolean expression x >= 0. Since x is currently storing the value
$ 5 $, this expression will evaluate to True. Therefore, we’ll move into the first block of statements in the if-else statement:
From here, we’ll print the message that the user’s input was a positive number, as well as the goodbye message at the end of the program. It will entirely skip the second block of statements in the if-else statement, as we can see here:
A full execution of this program is shown in the animation below:
Code Tracing Example - False
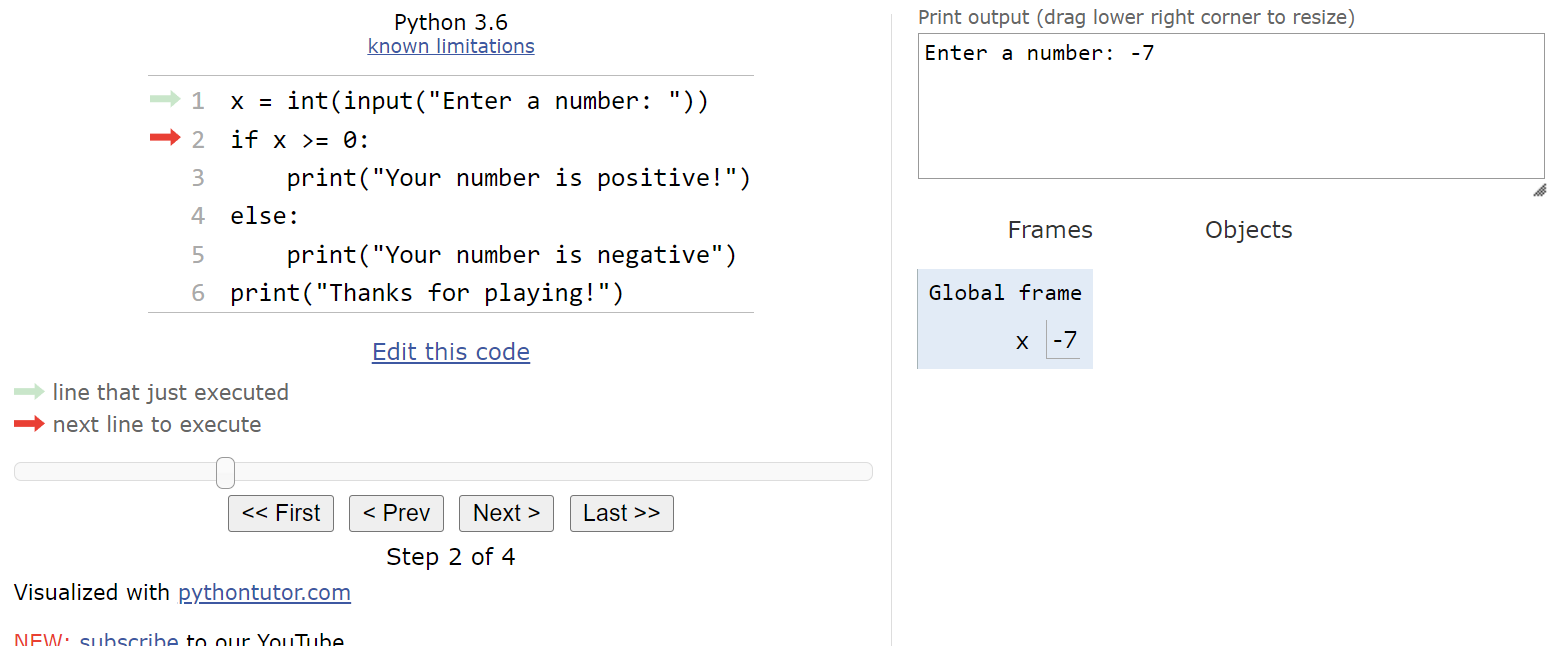
What if the user inputs a negative value, such as $ -7 $? In that case, we’ll be at this state in our program:
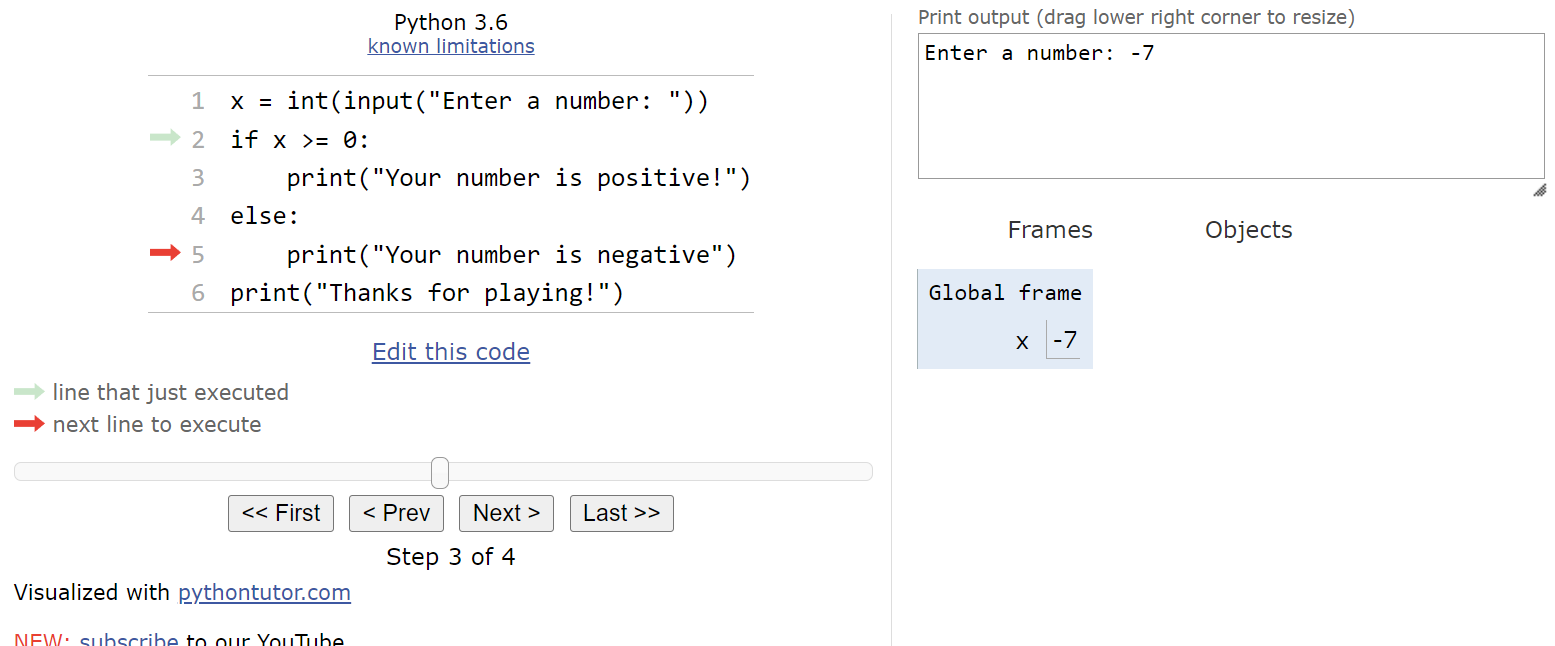
From here, we’ll evaluate the Boolean expression x >= 0 again. This time, however, we’ll see that it evaluates to False, so we’ll jump down to the second block of statements inside the if-else statement:
This will print a message to the user that the input was a negative number, and then it will print the goodbye message. We completely skipped the first block of statements:
A complete run through this program is shown in this animation:
So, as we expect, an if-else statement allows us to run one block of statements or the other, based on the value of the Boolean expression. It is a very powerful piece of code, and it allows us to write programs that perform different actions based on the input provided by the user or the values of other variables.
If-Else Statement Flowchart
Another way to visualize an if-else statement is using a flowchart. Consider the following Python code:
x = int(input("Input: " ))
if x >= 0:
print(x)
else:
print(-1 * x)
print("Goodbye")This code can also be represented as the flowchart shown below:
Once again, we start at the top of the flowchart at the circle labeled “START”. From there, we read an input from the user and store it in the variable x. At this point, we reach our if-else statement’s decision node, represented by the diamond. Here, we are using the Boolean expression x >= 0 to determine which branch to follow. So, if the user inputs a positive value, then we’ll follow the path to the right that is labeled “True”, which will simply print the value of x to the screen.
However, if the user inputs a negative value for x, then the Boolean expression will be False and we’ll follow the path to the left labeled “False”. In this branch, we’ll print the value of (-1 * x) to the screen, which simply removes the negative sign from the value in x.
Finally, after each path, we’ll merge back together to run the last piece of code, which prints the "Goodbye" message to the screen.
Notice that there is no way to print both x and -1 * x in the same execution of this program. If we follow the arrows through the flowchart, we see that we can only follow one branch or the other, and not both. This is an important concept to remember when working with if-else statements! The control flow of the program can only pass through one of the two blocks of statements, but not both.
Subsections of If-Else
Testing Branches & Paths
YouTube VideoResources
One important concept to understand when writing if statements and if-else statements is the control flow of the program. Before we learned about conditional statements, our programs had a linear control flow - there was exactly one pathway through the program, no matter what. Each time we ran the program, the same code would be executed each time in the same order. However, with the introduction of conditional statements, this is no longer the case.
Because of this, testing our programs becomes much more complicated. We cannot simply test it once or twice, but instead we should plan on testing our programs multiple times to make sure they work exactly the way we want. So, let’s go through some of the various ways we can test our programs that include conditional statements.
Simple Example
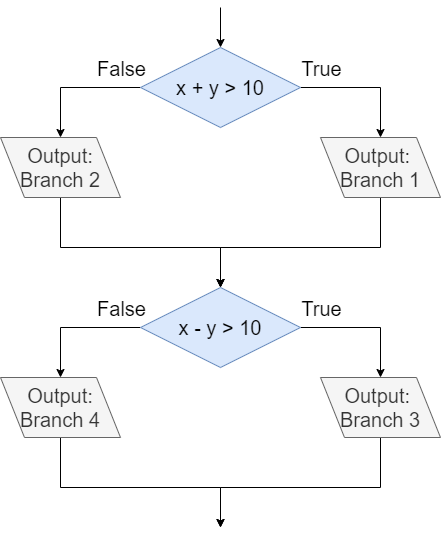
First, let’s consider this example program:
x = int(input("Enter a number: "))
y = int(input("Enter a number: "))
if x + y > 10:
print("Branch 1")
else:
print("Branch 2")
if x - y > 10:
print("Branch 3")
else:
print("Branch 4")We can represent the two if-else statements in this program in the following flowchart as well:
Branch Coverage
First, let’s consider how we can achieve branch coverage by executing all of the branches in this program. This means that we should test the program using different sets of inputs that will run different branches in the code. Our goal is to execute the code in each branch at least once. In this example, we see that there are four branches, helpfully labeled with the numbers one through four in the print() statements included in each branch.
So, let’s start with a simple set of inputs, which will store
$ 6 $ in both x and y. Which branches will be executed in this case? Before reading ahead, see if you can work through the code above and determine which branches are executed?
In the first if-else statement, we’ll see the x + y is equal to
$ 12 $, which is greater than
$ 10 $, making that Boolean statement True. So, we’ll execute the code in branch 1 this time through. When we reach the second if-else statement, we’ll compute the value of x - y to be
$ 0 $, which is less than
$ 10 $. In this case, that makes the Boolean statement False, so we’ll execute branch 4. Therefore, by providing the inputs 6 and 6, we’ve executed the code in branches 1 and 4.
So, can we think of a second set of inputs that will execute the code in branches 2 and 3? That can be a bit tricky - we want to come up with a set of numbers that add to a value less than
$ 10 $, but with a difference that is greater than
$ 10 $. However, we can easily do this using negative numbers! So, let’s assume that the user inputs
$ 6 $ for x and
$ -6 $ for y. When we reach the first if-else statement, we can compute the result of x + y, which is
$ 0 $. That is less than
$ 10 $, so the Boolean statement is False and we’ll execute the code in branch 2. So far, so good!
Next, we’ll reach the second if-else statement. Here, we’ll compute the result of x - y. This time, we know that
$ 6 - -6 $ is actually
$ 12 $, which is greater than
$ 10 $. So, since that Boolean expression is True, we’ll run the code in branch 3. That’s exactly what we wanted!
Therefore, if we want to test this program and try to execute all the branches, we only have to provide two pairs of inputs:
- $ 6 $ and $ 6 $
- $ 6 $ and $ -6 $
However, that’s only one way we can test our program. There are many other methods we can follow!
Path Coverage
A more thorough way to test our programs is to achieve path coverage. In this method, our goal is to execute all possible paths through the program. This means that we want to execute every possible ordering of branches! So, since our program has 4 branches in two different if-else statements, the possible orderings of branches are listed below:
- Branch 1 -> Branch 3
- Branch 1 -> Branch 4
- Branch 2 -> Branch 3
- Branch 2 -> Branch 4
As we can see, there are twice as many paths as there are branches in this case! We’ve already covered ordering 2 and 3 from this list, so let’s see if we can find inputs that will cover the other two orderings.
First, we want to find a set of inputs that will execute branch 1 followed by branch 3. So, we’ll need two numbers that add to a value greater than 10, but their difference is also greater than 10. So, let’s try the value
$ 12 $ for x and
$ 0 $ for y. In that case, their sum is greater than
$ 10 $, so we’ll execute branch 1 in the first if-else statement. When we reach the second if-else statement, we can evaluate x - y and find that it is also
$ 12 $, which is greater than
$ 10 $ and we’ll execute branch 3. So, we’ve covered the first ordering!
The last ordering can be done in a similar way - we need a pair of inputs with a sum less than
$ 10 $ and also a difference less than
$ 10 $. A simple answer would be to input
$ 4 $ for both x and y. In this case, their sum is
$ 8 $ and their difference is
$ 0 $, so we’ll end up executing branch 2 of the first if-else statement, and branch 4 of the second if-else statement. So, that covers the last ordering.
As we can see, path coverage will also include branch coverage, but it is a bit more difficult to achieve. If we want to cover all possible paths, we should test our program with these 4 sets of inputs now:
- $ 6 $ and $ 6 $
- $ 6 $ and $ -6 $
- $ 12 $ and $ 0 $
- $ 4 $ and $ 4 $
There’s still one more way we can test our program, so let’s try that out as well.
Edge Cases
Finally, we should also use a set of inputs that test the “edges” of the Boolean expressions used in each if-else statement. An edge is a value that is usually the smallest or largest value before the Boolean expression’s output would change. So, an edge case is simply a set of input values that are specifically created to be edges for the Boolean expressions in our code.
For example, let’s look at the first Boolean logic statement, x + y > 10. If we are simply considering whole numbers, then the possible edge cases for this Boolean expression are when the sum of x + y is exactly
$ 10 $ and
$ 11 $. When it is
$ 10 $ or below, the result of the Boolean expression is False, but when the result is
$ 11 $ or higher, then the Boolean expression is true. So,
$ 10 $ and
$ 11 $ represent the edge between True values and False values. The same applies to the Boolean expression in the second if-else statement.
So, to truly test the edge cases in this example, we should come up with a set of values with the sum and difference of exactly
$ 10 $ and exactly
$ 11 $. For the first one, a very easy solution would be to set x to
$ 10 $ and y to
$ 0 $. In this case, both the sum and the difference is
$ 10 $, so we’re on the False side of the edge. Our program will correctly execute branches 2 and 4.
For the other edge, we can use a similar set of inputs where x is
$ 11 $ and y is still
$ 0 $. In this case, both the sum and difference is
$ 11 $, so each Boolean expression will evaluate to True and we’ll execute branches 1 and 3.
Why is this important? To understand that, we must think a bit about what was intended by this program. What if the program should execute branches 1 and 3 if the value is greater than or equal to
$ 10 $? In that case, both of our chosen edge cases should execute branches 1 and 3, but instead we saw that the edge case
$ 10 $ executed branches 2 and 4 instead. This is a simple logic error that happens all the time in programming - we simply forgot to use the greater than or equal to symbol >= instead of the simple greater than symbol > in our code. So, a minor typo like that can change the entire execution of our program, and we wouldn’t have noticed it in any of our previous tests. This is why it is important to test the edge cases along with other inputs.
In fact, it would probably be a good idea to add a third edge case, where the sum and difference equal
$ 9 $, just to be safe. That way, we can clearly see the difference between True and False values in this program.
So, the final set of values we may want to test this program with are listed below:
- $ 6 $ and $ 6 $ (branch coverage 1 and 4)
- $ 6 $ and $ -6 $ (branch coverage 2 and 3)
- $ 12 $ and $ 0 $ (path coverage 1 and 3)
- $ 4 $ and $ 4 $ (path coverage 2 and 4)
- $ 9 $ and $ 0 $ (edge case 2 and 4)
- $ 10 $ and $ 0 $ (edge case 2 and 4)
- $ 11 $ and $ 0 $ (edge case 1 and 3)
As we can see, even a simple program with just a few lines of code can require substantial testing to really be sure it works correctly! This doesn’t even include other types of testing, where we make sure it works properly with invalid input values, decimal numbers, and other situations. That type of testing is really outside of the scope of this lab, but we’ll learn more about some of those topics later in this course.
Complex Example
Let’s go through one more example to get some more practice with creating test inputs for conditional statements. For this example, let’s consider the following program in Python:
a = int(input("Enter a number: "))
b = int(input("Enter a number: "))
if a // b >= 5:
# Branch 1
print(f"{b} goes into {a} at least 5 times")
else:
# Branch 2
print(f"{a} is less than 5 times {b}")
if a % b == 0:
# Branch 3
print(f"{b} evenly divides {a}")
else:
# Branch 4
print(f"{a} / {b} has a remainder")This program is a bit trickier to evaluate. First, it accepts two numbers as input. Then, it will check to see if the first number is at least 5 times the second number. It will print an appropriate message in either case. Then, it will check to see if the first number is evenly divided by the second number, and once again it will print a message in either case.
Branch Coverage
To achieve branch coverage, we need to come up with a set of inputs that will cause each print statement to be executed. Thankfully, the branches are numbered using comments in the Python code, so it is easy to keep track of them.
Let’s start with an easy input - we’ll set a to
$ 25 $ and b to
$ 5 $. This means that a // b is equal to
$ 5 $, so we’ll go into branch 1 in the first if statement. The second if statement will go into branch 3, since a % b is exactly
$ 0 $ because
$ 5 $ stored in b will evenly divide the
$ 25 $ stored in a without any remainder. So, we’ve covered branches 1 and 3 with this input.
For another input, we can choose
$ 21 $ for a and
$ 5 $ for b. In the first if statement, we’ll see that a // b is now
$ 4 $, so we’ll go into branch 2 instead. Likewise, in the second if statement we’ll execute branch 4, since a % b is equal to
$ 1 $ with these inputs. That means we’ve covered branches 2 and 4 with these inputs.
Therefore, we can achieve branch coverage with just two inputs:
- $ 25 $ and $ 5 $
- $ 21 $ and $ 5 $
Path Coverage
Recall that there are four paths through a program that consists of two if statements in a row:
- Branch 1 -> Branch 3
- Branch 1 -> Branch 4
- Branch 2 -> Branch 3
- Branch 2 -> Branch 4
We’ve already covered the first and last of these paths, so we must simply find inputs for the other two.
One input we can try is
$ 31 $ and
$ 5 $. In the first if statement, we’ll go to branch 1 since a // b will be
$ 6 $ this time. However, when we get to the second if statement, we’ll find that there is a remainder of
$ 1 $ after computing a % b, so we’ll go to branch 4 instead. This covers the second path.
The third path can be covered by inputs
$ 20 $ and
$ 5 $. In the first if statement, we’ll go to branch 2 because a // b is now
$ 4 $, but we’ll end up in branch 3 in the second if statement since a % b is exactly 0.
Therefore, we can achieve path coverage with these four inputs:
- $ 25 $ and $ 5 $
- $ 21 $ and $ 5 $
- $ 31 $ and $ 5 $
- $ 20 $ and $ 5 $
Edge Cases
What about edge cases? For the first if statement, we see the statement a // b >= 5, so that clues us into the fact that we’ll probably want to try values that result in the numbers
$ 4 $,
$ 5 $, and
$ 6 $ for this statement. Thankfully, if we look at the inputs we’ve already tried, we can see that this is already covered! By being a bit deliberate with the inputs we’ve been choosing, we can not only achieve branch and path coverage, but we can also choose values that test the edge cases for various Boolean expressions as well.
Likewise, the Boolean statement in the second if statement is a % b == 0, so we’ll want to try situations where a % b is exactly
$ 0 $, and when it is some other value. Once again, we’ve already covered both of these instances in our sample inputs!
So, with a bit of thinking ahead, we can come up with a set of just 4 inputs that not only achieve full path and branch coverage, but also properly test the various edge cases that are present in the program!
Subsections of Testing Branches & Paths
Conditionals Practice
Let’s try some simple practice problems. These problems are not graded - they are just for you to practice before doing the real exercises in the lab itself. You can find the answers below each question by clicking the button below each question.
4.5 Reading Code
Consider the following Python program:
a = int(input("Enter a whole number: "))
b = int(input("Enter a whole number: "))
if (a + b) % 3 == 0:
print("Branch 1")
else:
print("Branch 2")
a = a * 2
b = b * 3
if (a + b) % 3 == 0:
print("Branch 3")
else:
print("Branch 4")What output is printed when the user inputs the values $ 2 $ and $ 4 $?
4.6 Testing Code
Consider the program in the previous question. Write a set of possible inputs to the program that will achieve path coverage. For each set of inputs, identify which branches will be executed when that input is provided to the program.
Think carefully! The same if statement is executed twice with different values, but those values are related to each other.
4.7 Reading Code
Consider the following Python program:
x = int(input("Enter an integer: "))
y = int(input("Enter an integer: "))
if x * 5 > y:
print("Branch 1")
else:
print("Branch 2")
if y % 5 == x:
print("Branch 3")
else:
print("Branch 4")What output is displayed when the user inputs the values $ 4 $ and $ 29 $?
4.8 Testing Code
Consider the program in the previous question. Write a set of possible inputs to the program that will achieve path coverage. For each set of inputs, identify which branches will be executed when that input is provided to the program.
4.9 Writing Code
Write a complete Python that performs the following actions:
- Accept a single input from the user and convert it to an integer
- If the number is even, display “That is an even number”. If it is odd, display “That is an odd number”.
- If the number is negative, display “That is a negative number”. If it is zero or positive, display “That is a positive number”.
Your program should include at least two conditional statements.
4.10 Writing Code
Write a complete Python program in that file that performs the following actions:
- Accept a single string as input from the user
- If the string comes before the string “First” in lexicographic order, print “That comes before First”. If not, print “That comes after First”.
- If the string comes after the string “last” in lexicographic order, print “That comes after last”. If not, print “That comes before last”.
Recall that you can use Boolean comparators such as < and > to compare two strings in Python. Also, pay special attention to the capitalization of the words “First” and “last” in the description above.
Your program should include at least two conditional statements.
Bonus food for thought: look at your completed answer - is there a path that is not possible to actually test? Why is that?
Linear Conditionals
YouTube VideoResources
Conditional statements are a very powerful tool for programmers to use. So far in this lab, we’ve explored simple conditional statements, including the if statement and if-else statement in Python. However, up to this point we’ve only looked at how we can use a single conditional statement at a time in a program, which can be very limiting. Now we’re going to explore how we can combine conditional statements in a variety of different ways to build even more complex programs. These combined, or nested conditional statements, are commonly used across all programming languages, but learning how to build and debug them takes time and practice. We’ll work through several examples, and then you’ll get a chance to try it yourself.
Linear Conditional Statements
To explore the various ways we can use conditional statements in code, let’s start by examining the same problem using three different techniques. We’ll use the classic Rock Paper Scissors game. In this game, two players simultaneously make one of three hand gestures, and then determine a winner based on the following diagram:
For example, if the first player displays a balled fist, representing rock and the second player displays a flat hand, representing paper, then the second player wins because “paper covers rock” according to the rules. If the players both display the same symbol, the game is considered a tie.
So, to make this work, we’re going to write a Python program that reads two inputs representing the symbols, and then we’ll use some conditional statements to determine which player wins. A basic skeleton of this program is shown below:
p1 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 1: ")
p2 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 2: ")
# determine the winnerOur goal, therefore, is to replace the comment # determine the winner with a set of conditional statements and print statements to accomplish this goal.
Linear Conditional Statements
First, let’s try to write this program using what we already know. We’ve already learned how to use conditional statements, and it is completely possible to write this program using just a set of linear conditional statements and nothing else. So, to do this, we need to determine each possible combination of inputs, and then write an if statement for each one. Since there are $ 3 $ possible inputs for each player, we know there are $ 3 * 3 = 9 $ possible combinations:
| Player 1 | Player 2 | Output |
|---|---|---|
| rock | rock | tie |
| rock | paper | player 2 wins |
| rock | scissors | player 1 wins |
| paper | rock | player 1 wins |
| paper | paper | tie |
| paper | scissors | player 2 wins |
| scissors | rock | player 2 wins |
| scissors | paper | player 1 wins |
| scissors | scissors | tie |
We also have to deal with a final option where one player or the other inputs an invalid value. So, in total, we’ll have $ 10 $ conditional statements in our program!
Let’s first try to make a quick flowchart of this program. Since we need $ 10 $ conditional statements, our flowchart will have $ 10 $ of the diamond-shaped decision nodes. Unfortunately, that would make a very large flowchart, so we’ll only include the first three decision nodes in the flowchart shown here:
As we can see, this flowchart is very tall, and just consists of one decision node after another. Thankfully, we should know how to implement this in code based on what we’ve previously learned. Below is a full implementation of this program in Python, using just linear conditional statements:
p1 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 1: ")
p2 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 2: ")
if p1 == "rock" and p2 == "rock":
print("tie")
if p1 == "rock" and p2 == "paper":
print("player 2 wins")
if p1 == "rock" and p2 == "scissors":
print("player 1 wins")
if p1 == "paper" and p2 == "rock":
print("player 1 wins")
if p1 == "paper" and p2 == "paper":
print("tie")
if p1 == "paper" and p2 == "scissors":
print("player 2 wins")
if p1 == "scissors" and p2 == "rock":
print("player 2 wins")
if p1 == "scissors" and p2 == "paper":
print("player 1 wins")
if p1 == "scissors" and p2 == "scissors":
print("tie")
if not (p1 == "rock" or p1 == "paper" or p1 == "scissors") or not (p2 == "rock" or p2 == "paper" or p2 == "scissors"):
print("error")This program seems a bit complex, but if we step through it one step at a time it should be easy to follow. For example, if the user inputs "scissors" for player 1 and "rock" for player 2, we just have to find the conditional statement that matches that input and print the correct output. Since we were careful about how we wrote the Boolean expressions for these conditional statements, we know that it is only possible for one of them to evaluate to true. So, we’d say that those Boolean expressions are mutually exclusive, since it is impossible for two of them to be true at the same time.
Things get a bit more difficult in the last conditional statement. Here, we want to make sure the user has not input an invalid value for either player. Unfortunately, the only way to do that using linear conditional statements is to explicitly check each possible value and make sure that the user did not input that value. This can seem pretty redundant, and it indeed is! As we’ll see later in this lab, there are better ways we can structure this program to avoid having to explicitly list all possible inputs when checking for an invalid one.
Before moving on, it is always a good idea to run this code yourself, either directly in Python or using Python Tutor, to make sure you understand how it works and what it does.
Alternative Version
There is an alternative way we can write this program using linear if statements. Instead of having an if statement for each possible combination of inputs, we can instead have a single if statement for each possible output, and construct more complex Boolean expressions that are used in each if statement. Here’s what that would look like in Python:
p1 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 1: ")
p2 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 2: ")
if (p1 == "rock" and p2 == "rock") or (p1 == "paper" and p2 == "paper") or (p1 == "scissors" and p2 == "scissors"):
print("tie")
if (p1 == "rock" and p2 == "paper") or (p1 == "paper" and p2 == "scissors") or (p1 == "scissors" and p2 == "rock"):
print("player 2 wins")
if (p1 == "rock" and p2 == "scissors") or (p1 == "paper" and p2 == "rock") or (p1 == "scissors" and p2 == "paper"):
print("player 1 wins")
if not (p1 == "rock" or p1 == "paper" or p1 == "scissors") or not (p2 == "rock" or p2 == "paper" or p2 == "scissors"):
print("error")In this example, we now have just four if statements, but each one now requires a Boolean expression that includes multiple parts. So, this program is simultaneously more and less complex than the previous example. It has fewer lines of code, but each line can be much trickier to understand and debug.
Again, feel free to run this code in either Python Tutor or directly in Python to confirm that it works and make sure you understand it before continuing.
In terms of style, both of these options are pretty much equivalent - there’s no reason to choose one over the other. However, we’ll see later in this lab, there are much better ways we can write this program using chaining and nesting with conditional statements.
The Python programming language has its own style guide, known as “PEP 8” to most Python programmers. One of the major conventions proposed in that guide is limiting the length of each line of code to just 79 characters, in order to make the code more readable. However, as we’ve seen above, it is very easy to exceed that length when dealing with complex Boolean expressions, and we’ll see this again as we add multiple levels of indentation when we nest conditional statements.
In this course, we won’t worry about line length, even though some text editors may mark those lines as being incorrect in Python. Likewise, in many examples we won’t wrap the lines to a shorter length, except for readability purposes in the videos and slides.
That said, it’s definitely a good style to try and follow, and we encourage you to think about ways you can write your code to keep it as concise and readable as possible. Having shorter lines of code, while still using descriptive variable and function names, is a good start!
File:Rock-paper-scissors.svg. (2020, November 18). Wikimedia Commons, the free media repository. Retrieved 16:57, February 28, 2022 from https://commons.wikimedia.org/w/index.php?title=File:Rock-paper-scissors.svg&oldid=513212597. ↩︎
Subsections of Linear Conditionals
Chaining Conditionals
YouTube VideoResources
In the previous example, we saw a set of linear if statements to represent a Rock Paper Scissors game. As we discussed on that page, the Boolean expressions are meant to be mutually exclusive, meaning that only one of the Boolean expressions will be true no matter what input the user provides.
When we have mutually exclusive Boolean expressions like this, we can instead use if-else statements to make the mutually exclusive structure of the program clearer to the user. Let’s see how we can do that.
Chaining Conditional Statements
To chain conditional statements, we can simply place the next conditional statement on the False branch of the first statement. This means that, if the first Boolean expression is True, we’ll execute the True branch, and then jump to the end of the entire statement. If it is False, then we’ll go to the False branch and try the next conditional statement. Here’s what this would look like in a flowchart:
This flowchart is indeed very similar to the previous one, but with one major change. Now, if any one of the Boolean expressions evaluates to True, that branch will be executed and then the control flow will immediately drop all the way to the end of the program, without ever testing any of the other Boolean expressions. This means that, overall, this program will be a bit more efficient than the one with linear conditional statements, because on average it will only have to try half of them before the program ends.
Now let’s take a look at what this program would look like in Python:
p1 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 1: ")
p2 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 2: ")
if p1 == "rock" and p2 == "rock":
print("tie")
else:
if p1 == "rock" and p2 == "paper":
print("player 2 wins")
else:
if p1 == "rock" and p2 == "scissors":
print("player 1 wins")
else:
if p1 == "paper" and p2 == "rock":
print("player 1 wins")
else:
if p1 == "paper" and p2 == "paper":
print("tie")
else:
if p1 == "paper" and p2 == "scissors":
print("player 2 wins")
else:
if p1 == "scissors" and p2 == "rock":
print("player 2 wins")
else:
if p1 == "scissors" and p2 == "paper":
print("player 1 wins")
else:
if p1 == "scissors" and p2 == "scissors":
print("tie")
else:
if not (p1 == "rock" or p1 == "paper" or p1 == "scissors") or not (p2 == "rock" or p2 == "paper" or p2 == "scissors"):
print("error")As we can see, this program is basically the same code as the previous program, but with the addition of a number of else keywords to place each subsequent conditional statement into the False branch of the previous one. In addition, since Python requires us to add a level of indentation for each conditional statement, we see that this program very quickly becomes difficult to read. In fact, the last Boolean expression is so long that it doesn’t even fit well on the screen!
We can make a similar change to the other example on the previous page:
p1 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 1: ")
p2 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 2: ")
if (p1 == "rock" and p2 == "rock") or (p1 == "paper" and p2 == "paper") or (p1 == "scissors" and p2 == "scissors"):
print("tie")
else:
if (p1 == "rock" and p2 == "paper") or (p1 == "paper" and p2 == "scissors") or (p1 == "scissors" and p2 == "rock"):
print("player 2 wins")
else:
if (p1 == "rock" and p2 == "scissors") or (p1 == "paper" and p2 == "rock") or (p1 == "scissors" and p2 == "paper"):
print("player 1 wins")
else:
if not (p1 == "rock" or p1 == "paper" or p1 == "scissors") or not (p2 == "rock" or p2 == "paper" or p2 == "scissors"):
print("error")Again, this results in very long lines of code, but it still makes it easy to see that the program is built in the style of mutual exclusion, and only one of the True branches will be executed. As before, feel free to run these programs directly in Python or using Python Tutor to confirm they work and that you understand how they work before continuing.
The Final Case
Now that we’ve built a program structure that enforces mutual exclusion, we’ll might notice something really interesting - the final if statement is no longer required! This is because we’ve already exhausted all other possible situations, so the only possible case is the last one. In that case, we can remove that entire statement and just replace it with the code from the True branch. Here’s what that would look like in Python:
p1 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 1: ")
p2 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 2: ")
if p1 == "rock" and p2 == "rock":
print("tie")
else:
if p1 == "rock" and p2 == "paper":
print("player 2 wins")
else:
if p1 == "rock" and p2 == "scissors":
print("player 1 wins")
else:
if p1 == "paper" and p2 == "rock":
print("player 1 wins")
else:
if p1 == "paper" and p2 == "paper":
print("tie")
else:
if p1 == "paper" and p2 == "scissors":
print("player 2 wins")
else:
if p1 == "scissors" and p2 == "rock":
print("player 2 wins")
else:
if p1 == "scissors" and p2 == "paper":
print("player 1 wins")
else:
if p1 == "scissors" and p2 == "scissors":
print("tie")
else:
# All other options have been checked
print("error")In this code, there is a comment showing where the previous if statement was placed, and now it simply prints an error. Again, this is possible because we’ve tried every possible valid combination of inputs in the previous Boolean expressions, so all that is left is invalid input. Try it yourself! See if you can come up with any valid input that isn’t already handled by the Boolean expressions - there shouldn’t be any of them.
Elif Keyword
To help build programs that include chaining conditional statements, Python includes a special keyword elif for this exact situation. The elif keyword is a shortened version of else if, and it means to replace the situation where an if statement is directly placed inside of an else branch. So, when we are chaining conditional statements, we can now do so without adding additional levels of indentation.
Here’s what the previous example looks like when we use the elif keyword in Python:
p1 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 1: ")
p2 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 2: ")
if p1 == "rock" and p2 == "rock":
print("tie")
elif p1 == "rock" and p2 == "paper":
print("player 2 wins")
elif p1 == "rock" and p2 == "scissors":
print("player 1 wins")
elif p1 == "paper" and p2 == "rock":
print("player 1 wins")
elif p1 == "paper" and p2 == "paper":
print("tie")
elif p1 == "paper" and p2 == "scissors":
print("player 2 wins")
elif p1 == "scissors" and p2 == "rock":
print("player 2 wins")
elif p1 == "scissors" and p2 == "paper":
print("player 1 wins")
elif p1 == "scissors" and p2 == "scissors":
print("tie")
else:
# All other options have been checked
print("error")There we go! That’s much easier to read, and in fact it is much closer to the examples of linear conditionals on the previous page. This is the exact same program as before, but now it is super clear that we are dealing with a mutually exclusive set of Boolean expressions. And, we can still have a single else branch at the very end that will be executed if none of the Boolean expressions evaluates to True.
A structure of mutually exclusive statements like this is very commonly used in programming, and Python makes it very simple to build using the elif keyword.
Using chained conditional statements like this makes it easy to detect and handle errors in the final else block, since all other options have already been checked. However, some programmers prefer to explicitly check for errors in the input at the start of the code, before any other work is done. This is especially common when working with loops to prompt the user for new input in case of an error, which we’ll learn about in a later lab.
When you are reading code, it is important to check both the start and end of a block of code when looking for possible error checks, since they could be included in either place. Recognizing common coding styles and conventions such as where to check for errors will help us better understand code written by others, and also make our code more readable by others.
Subsections of Chaining Conditionals
Nesting Conditionals
YouTube VideoResources
We’ve already seen how we can chain conditional statements by placing a new conditional statement inside of the False branch of another conditional statement. If we think about that, however, that implies that we probably should be able to place conditional statements inside of the True branch as well, or really anywhere. As it turns out, that’s exactly correct. We call this nesting, and it is really quite similar to what we’ve already seen in this lab.
Using nested conditional statements, we can really start to rethink the entire structure of our program and greatly simplify the code. Let’s take a look at how we can do that with our Rock Paper Scissors game.
Nesting Conditional Statements
In our Rock Paper Scissors game, we are really checking the value of two different variables, p1 and p2. In all of our previous attempts, we built complex Boolean expressions that checked the values of both variables in the same expression, such as p1 == "rock" and p2 == "scissors". What if we simply checked the value of one variable at a time, and then used nested conditional statements in place of the and operator? What would that look like?
Here’s an example of a Rock Paper Scissors game that makes use of nested conditional statements:
Here, we begin by checking if the value in p1 is "rock". If it is, then we’ll go to the True branch, and start checking the values of p2. If p2 is also "rock", then we know we have a tie and we can output that result. If not, we can check to see if it is "paper" or "scissors", and output the appropriate result. If none of those are found, then we have to output an error.
In the False branch of the first conditional statement, we know that p1 is not "rock", so we’ll have to check if it is "paper" and "scissors". Inside of each of those conditional statements, we’ll also have to check the value of p2, so we’ll end up with a significant number of conditional statements in total!
Let’s see what such a program would look like in Python:
p1 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 1: ")
p2 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 2: ")
if p1 == "rock":
if p2 == "rock":
print("tie")
elif p2 == "paper":
print("player 2 wins")
elif p2 == "scissors":
print("player 1 wins")
else:
print("error")
elif p1 == "paper":
if p2 == "rock":
print("player 1 wins")
elif p2 == "paper":
print("tie")
elif p2 == "scissors":
print("player 2 wins")
else:
print("error")
elif p1 == "scissors":
if p2 == "rock":
print("player 2 wins")
elif p2 == "paper":
print("player 1 wins")
elif p2 == "scissors":
print("tie")
else:
print("error")
else:
print("error") In this example, we have an outer set of chained conditional statements checking the value of p1, and then each of the branches will check the value of p2 and determine which output is correct. It is very similar in structure to the chained conditional example on the previous page, just laid out a bit differently. As before, try running this program yourself in either Python or Python Tutor to make sure it works and you understand how it is structured.
Removing Duplicate States
Looking at this code, one thing we might quickly notice is that we now have four places that print "error" instead of just one. This is because we now have to check the values of p2 in three separate places, and can’t simply assume that the final else case in the outermost conditional statement is the only case where an error might be found.
One way we can simplify this code is by including a specific conditional statement just to check for any error situations, and handle those upfront before the rest of the code. So, we can rewrite this code as shown here to accomplish that:
p1 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 1: ")
p2 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 2: ")
if not (p1 == "rock" or p1 == "paper" or p1 == "scissors") or not (p2 == "rock" or p2 == "paper" or p2 == "scissors"):
print("error")
else:
if p1 == "rock":
if p2 == "rock":
print("tie")
elif p2 == "paper":
print("player 2 wins")
else:
print("player 1 wins")
elif p1 == "paper":
if p2 == "rock":
print("player 1 wins")
elif p2 == "paper":
print("tie")
else:
print("player 2 wins")
else:
if p2 == "rock":
print("player 2 wins")
elif p2 == "paper":
print("player 1 wins")
else:
print("tie")By confirming that both p1 and p2 only contain either "rock", "paper", or "scissors" first, we can then make some pretty handy assumptions later in our code. For example, now the outermost conditional statement only explicitly checks if p1 contains "rock" or "paper", and then the third block is simply an else clause by itself. We can do this because we already know that "scissors" is the only other possible value that can be stored in p1, so we don’t have to explicitly check for it. We can make similar changes to the nested conditional statements as well. So, just by adding one complex Boolean expression and conditional statement to our program, we were able to remove 4 that we no longer needed!
Further Simplification
In fact, we can even take this one step further. Now that we know that both p1 and p2 only contain valid values, we can easily determine if that match has ended in a tie by simply checking if the variables contain the same value. So, with a bit of restructuring, we can simplify our program as shown here:
p1 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 1: ")
p2 = input("Enter \"rock\", \"paper\", or \"scissors\" for player 2: ")
if not (p1 == "rock" or p1 == "paper" or p1 == "scissors") or not (p2 == "rock" or p2 == "paper" or p2 == "scissors"):
print("error")
else:
if p1 == p2:
print("tie")
elif p1 == "rock":
if p2 == "paper":
print("player 2 wins")
else:
print("player 1 wins")
elif p1 == "paper":
if p2 == "rock":
print("player 1 wins")
else:
print("player 2 wins")
else:
if p2 == "rock":
print("player 2 wins")
else:
print("player 1 wins")This code presents a clear, easy to read version of a Rock Paper Scissors program. At the top, we receive input from the users, and then the first conditional statement is used to determine if the input is valid. If not, it will print an error.
If the input is valid, then we can make some assumption about the various possible inputs in our program’s logic, which greatly reduced the number of conditional statements. We are also checking for ties at the beginning, so in the False branch of that conditional statement we can also assume that the values in p1 and p2 are different, further reducing the number of items we have to check.
We’ll revisit this example later in this course to show how we can convert the first conditional statement into a loop, which will prompt the user for new input if an invalid input is provided. This will make our program even better and easier for anyone to use.
Subsections of Nesting Conditionals
Blocks & Scope
YouTube VideoResources
Now that we’ve seen how we can chain and nest multiple conditional statements in our code, we need to address a very important concept: variable scope.
In programming, variable scope refers to the locations in code where variables can be accessed. Contrary to what we may think based on our experience, when we declare a variable in our code, it may not always be available everywhere. Instead, we need to learn the rules that determine where variables are available and why.
Many Languages: Block Scope
The example below demonstrates block scope, which is NOT how Python handles scope. We are using Python code so the example is understandable, but Python handles scope differently. See the next section for how Python actually handles scope.
First, let’s talk about the most common type of variable scope, which is block scope. This type of variable scope is used in many programming languages, such as Java, C#, C/C++, and more. In block scope, variables are only available within the blocks where they are declared, including any other blocks nested within that block. Also, variables can only be accessed by code executed after the variable is initially declared or given a value.
So, what is a block? Effectively, each function and conditional statement introduces a new block in the program. In languages such as Java and C/C++, blocks are typically surrounded by curly braces {}. In Python, blocks are indicated by the level of indentation.
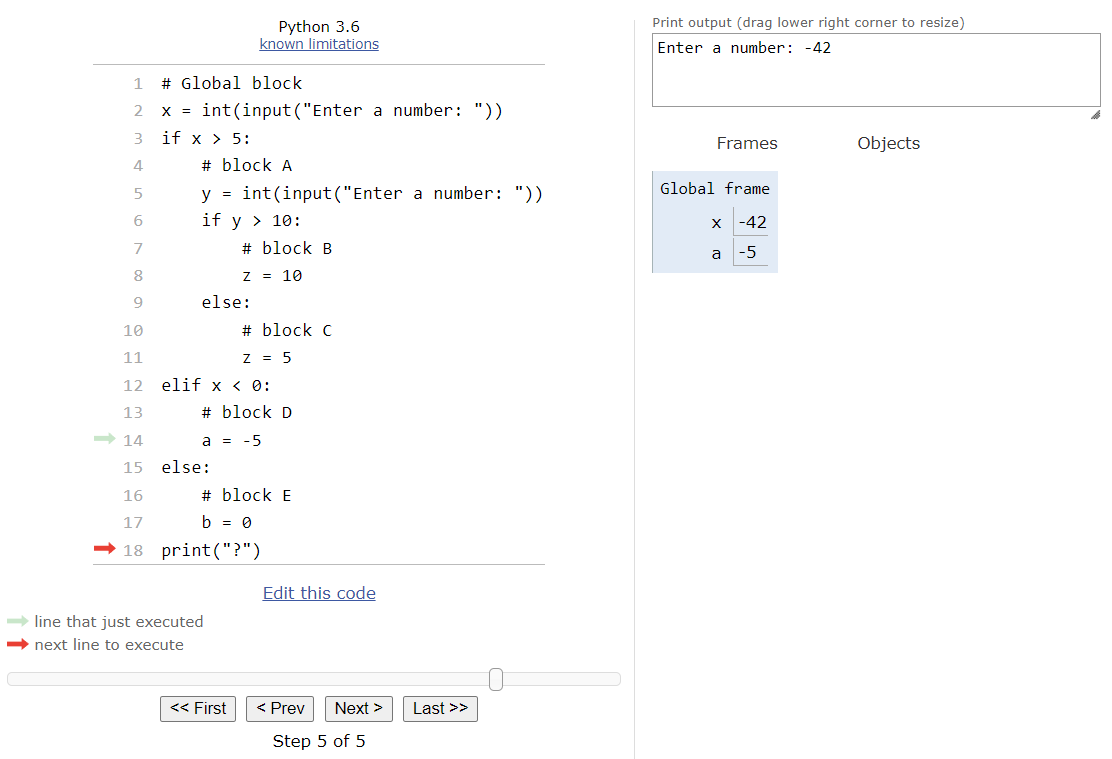
For example, consider the following Python code:
# Global block
x = int(input("Enter a number: "))
if x > 5:
# block A
y = int(input("Enter a number: "))
if y > 10:
# block B
z = 10
else:
# block C
z = 5
elif x < 0:
# block D
a = -5
else:
# block E
b = 0
print("?")This program contains six different blocks of code:
- The
Globalblock, which is all of the code at the top level of the file - Block
A, which is all of the code inside of theTruebranch of the outermost conditional statement. - Block
B, theTruebranch of the inner conditional statement - Block
C, theFalsebranch of the inner conditional statement - Block
D, theTruebranch of the firstelifclause of the outer conditional statement - Block
E, theFalsebranch of the outermost conditional statement
Inside of each of those blocks, we see various variables that are declared. For example, the variable x is declared in the Global block. So, with block scope, this means that the variable x is accessible anywhere inside of that block, including any blocks nested within it.
Below is a list of all of the variables in this program, annotated with the blocks where that variable is accessible in block scope:
x- blocksGlobal,A,B,C,D,Ey- blocksA,B,Cz- blocksBandCmore on this latera- blockDb- blockE
One thing that is unique about this example is the variable z, which is declared in both block B and block C. What does this mean when we are dealing with block scope? Basically, those variables named z are actually two different variables! Since they cannot be accessed outside of the block that they are declared in, they should really be considered as completely separate entities, even though they are given the same name. This is one of the trickiest concepts when dealing with scope!
So, if this program is using block scope, what variables can be printed at the very end of the program, where the question mark ? is found in a print() statement? In this case, only the variable x exists in the Global block’s scope, so it is the only variable that we can print at the end of the program.
If we want to print the other variables, we must declare them in the appropriate scope. So, we can update our code as shown here to do that:
# Global block
# variable declarations in Global block
y = 0
z = 0
a = 0
b = 0
x = int(input("Enter a number: "))
if x > 5:
# block A
y = int(input("Enter a number: "))
if y > 10:
# block B
z = 10
else:
# block C
z = 5
elif x < 0:
# block D
a = -5
else:
# block E
b = 0
print("?")With this change, we can now access all of the variables in the Global scope, so any one of them could be printed at the end of the program. This also has the side effect of making the variable z in both blocks B and C the same variable, since it is now declared at a higher scope.
Python: Function Scope
Python, however, uses a different type of variable scope known as function scope. In function scope, variables that are declared anywhere in a function are accessible everywhere in that function as soon as they’ve been declared or given a value. In Python, the Global scope is treated the same as a function’s scope, so variables declared in the Global scope in Python are accessible everywhere. So, once we see a variable in the code while we’re executing within a function or in the Global scope, we can access that variable anywhere within the same scope.
We haven’t introduced functions in Python quite yet, but it is important to go ahead and use the correct terminology here. For now, you can think of everything as being part of the “Global” function in Python. We’ll revisit this concept later when we introduce functions.
Let’s go back to the previous example, and look at that in terms of function scope
# Global block
x = int(input("Enter a number: "))
if x > 5:
# block A
y = int(input("Enter a number: "))
if y > 10:
# block B
z = 10
else:
# block C
z = 5
elif x < 0:
# block D
a = -5
else:
# block E
b = 0
print("?")Using function scope, any of the variables x, y, z, a or b could be placed in the print() statement at the end of the code, and the program could work. However, there is one major caveat that we must keep in mind: we can only print the variable if it has been given a value in the program!
For example, if the user inputs a negative value for x, then the variables y, z, and b are never given a value! We can confirm this by running the program in Python Tutor. As we see here, at the end of the program, only the variables x and a are shown in the list of variables within the Global frame in Python Tutor on the right:
Because of this, we have to be careful when we write our programs in Python using function scope. It is very easy to find ourselves in situations where our program will work most of the time, since it usually executes the correct blocks of code to populate the variables we need, but there may be situations where that isn’t guaranteed.
This is where testing techniques such as path coverage are so important. If we have a set of inputs that achieve path coverage, and we are able to show that the variables we need are available at the end of the program in each of those paths, then we know that we can use them.
Alternatively, we can build our programs in Python as if Python used block scope instead of function scope. By assuming that variables are only available in the blocks where they are given a value, we can always ensure that we won’t reach a situation where we are trying to access a variable that isn’t available. For novice programmers, this is often the simplest option.
Dealing with scope is a tricky part of learning to program. Thankfully, in Python, as well as many other languages, we can easily use tools such as Python Tutor and good testing techniques to make sure our programs are well written and won’t run into any errors related to variable scope.
Subsections of Blocks & Scope
Worked Example
YouTube VideoResources
Let’s go through another worked example to see how we can translate a problem statement into a working program. We’ll also take a look at how we can test the program to verify that it is working as intended.
Problem Statement
Here’s a short and simple game that can be played by three players:
Three players each guess a positive integer greater than $ 0 $, and then share them simultaneously. The winner is chosen following this formula:
- If any two players have chosen the same number, the game is a tie.
- If all players have chosen even numbers, or all players have chosen odd numbers, then the smallest number wins.
- Otherwise, the largest number wins.
This game has some similarities to Rock Paper Scissors, but the logic is quite a bit different. So, let’s work through how we would build this program using conditional statements.
Initial Program
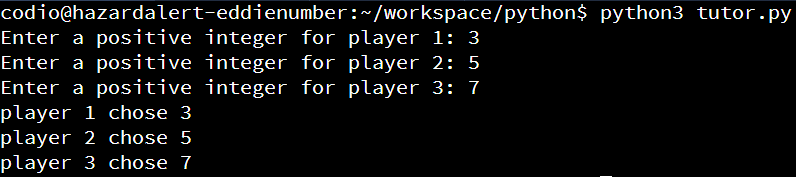
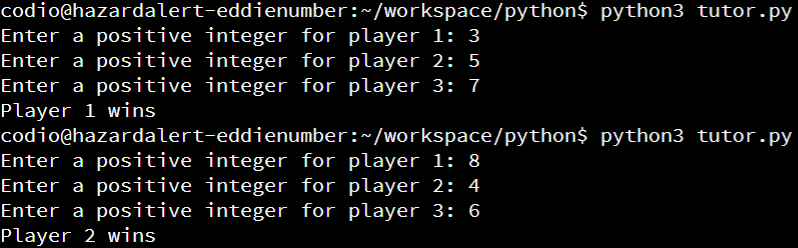
Our first step should be to build a simple program that handles user input. So, we’ll create a new Python program that contains three variables to store user input. We’ll also use the input() function to read input, and the int() function to convert each input to an integer. Below that, we’ll add some print statements for testing. At this point, our program should look similar to this:
p1 = int(input("Enter a positive integer for player 1: "))
p2 = int(input("Enter a positive integer for player 2: "))
p3 = int(input("Enter a positive integer for player 3: "))
# debugging statements
print(f"player 1 chose {p1}")
print(f"player 2 chose {p2}")
print(f"player 3 chose {p3}")With this code in place, we’ve already created a Python program that we can run and test. So, before moving on, let’s run this program at least once to verify that it works correctly. This will help us quickly detect and correct any initial errors in our program, and make it much easer to debug logic errors later on.
So, when we run this program, we should see output similar to this:
Checking for Valid Input
Now that we have confirmed our program is working, let’s start writing the logic in this program. Deciding which conditional statement to write first is a very important step in designing a program, but it is difficult to learn what works best without lots of practice. If we look at the problem statement above, we see that there are several clear conditions that we’ll have to check:
- Are the numbers all even?
- If so, which number is smallest?
- Are the numbers all odd?
- If so, which number is smallest?
- Are the numbers not all even or odd?
- If so, which number is largest?
However, there is one more condition that we should also keep in mind. This one isn’t clearly stated in the rules, but implied in the problem statement itself:
- Are all numbers greater than $ 0 $?
So, to write an effective program, we should first make sure that all of the inputs are greater than $ 0 $. We can do this using a simple conditional statement. We’ll also remove our debugging statements, as they are no longer needed:
p1 = int(input("Enter a positive integer for player 1: "))
p2 = int(input("Enter a positive integer for player 2: "))
p3 = int(input("Enter a positive integer for player 3: "))
if p1 <= 0 or p2 <= 0 or p3 <= 0:
print("Error")
else:
print("All numbers are greater than 0")In this conditional statement, we are checking to see if any one of the numbers is less than or equal to $ 0 $. Of course, using some Boolean algebra and De Morgan’s law, we can see that this is equivalent to checking if all numbers are not greater than $ 0 $. Either approach is valid.
Checking for Ties
Once we know we have valid input, the next step in determining a winner is to first determine if there are any ties. For this, we simply need to check if any two players input the same number. Since there are three players, we need to have three different Boolean expressions to accomplish this. In our program, we could add a conditional statement as shown here:
p1 = int(input("Enter a positive integer for player 1: "))
p2 = int(input("Enter a positive integer for player 2: "))
p3 = int(input("Enter a positive integer for player 3: "))
if p1 <= 0 or p2 <= 0 or p3 <= 0:
print("Error")
elif p1 == p2 or p2 == p3 or p3 == p1:
print("Tie")
else:
print("Not a Tie")This is a pretty simple Boolean expression that will check and see if any possible pair of inputs is equal. We use the or Boolean operator here since any one of those can be true in order for the whole game to be a tie.
All Odds or Evens
Next, let’s tackle whether the inputs are all odds or all evens. If we look at the rules above, this seems to be the next most logical thing we’ll need to know in order to determine the winner of the game. Recall that we can determine if a number is even or odd by using the modulo operator % and the number
$ 2 $. If that result is
$ 0 $, the number is even. If not, the number is odd.
In code, we can express that in a conditional statement as shown here:
p1 = int(input("Enter a positive integer for player 1: "))
p2 = int(input("Enter a positive integer for player 2: "))
p3 = int(input("Enter a positive integer for player 3: "))
if p1 <= 0 or p2 <= 0 or p3 <= 0:
print("Error")
elif p1 == p2 or p2 == p3 or p3 == p1:
print("Tie")
elif p1 % 2 == 0 and p2 % 2 == 0 and p3 % 2 == 0:
print("All numbers are even")
elif p1 % 2 != 0 and p2 % 2 != 0 and p3 % 2 != 0:
print("All numbers are odd")
else:
print("Numbers are both even and odd")Notice that we are using the and Boolean operator in these conditional statements, because we want to be sure that all numbers are either even or odd.
In this example, we’re also choosing to use chained conditional statements with the elif keyword instead of nesting the conditionals. This helps clearly show that each outcome is mutually exclusive from the other outcomes.
However, we chose to nest the program logic inside of the outermost conditional statement, which checks for valid input. This helps us clearly see the part of the program that is determining who wins the game, and the part of the program that is validating the input. Later on, we’ll see how we can rewrite that conditional statement into a loop to prompt the user for new input, so it makes sense for us to keep it separate for now.
Determining the Smallest Number
Once we know if the numbers are either all even or all odd, we know that the winning number is the smallest number of the three inputs. So, how can we determine which number is the smallest? We can use a couple of nested conditional statements!
Let’s handle the situation where all numbers are even first. We know that the smallest number must be smaller than both other numbers. So, we can use a couple of Boolean expressions to check if that is the case for each number:
p1 = int(input("Enter a positive integer for player 1: "))
p2 = int(input("Enter a positive integer for player 2: "))
p3 = int(input("Enter a positive integer for player 3: "))
if p1 <= 0 or p2 <= 0 or p3 <= 0:
print("Error")
elif p1 == p2 or p2 == p3 or p3 == p1:
print("Tie")
elif p1 % 2 == 0 and p2 % 2 == 0 and p3 % 2 == 0:
if p1 < p2 and p1 < p3:
print("Player 1 wins")
elif p2 < p1 and p2 < p3:
print("Player 2 wins")
else:
print("Player 3 wins")
elif p1 % 2 != 0 and p2 % 2 != 0 and p3 % 2 != 0:
print("All numbers are odd")
else:
print("Numbers are both even and odd")Here, we start by checking if player 1’s number is smaller than both player 2’s and player 3’s. If so, then player 1 is the winner. If not, we do the same for player 2’s number. If neither player 1 nor player 2 has the smallest number, then we can assume that player 3 is the winner without even checking.
As it turns out, we would end up using the exact same code in the situation where all numbers are odd, so for now we can just copy and paste that set of conditional statements there as well:
p1 = int(input("Enter a positive integer for player 1: "))
p2 = int(input("Enter a positive integer for player 2: "))
p3 = int(input("Enter a positive integer for player 3: "))
if p1 <= 0 or p2 <= 0 or p3 <= 0:
print("Error")
elif p1 == p2 or p2 == p3 or p3 == p1:
print("Tie")
elif p1 % 2 == 0 and p2 % 2 == 0 and p3 % 2 == 0:
if p1 < p2 and p1 < p3:
print("Player 1 wins")
elif p2 < p1 and p2 < p3:
print("Player 2 wins")
else:
print("Player 3 wins")
elif p1 % 2 != 0 and p2 % 2 != 0 and p3 % 2 != 0:
if p1 < p2 and p1 < p3:
print("Player 1 wins")
elif p2 < p1 and p2 < p3:
print("Player 2 wins")
else:
print("Player 3 wins")
else:
print("Numbers are both even and odd")That covers the situations where all players have input either even or odd numbers. We can quickly test this program a couple of times by providing various inputs that match those cases. So, when we run this program, we should see output like this:
Determining the Largest Number
The last step is to determine the largest number in the case that the numbers are not all even or odd. Since we’ve already written some code to handle the opposite case, let’s quickly copy and tweak that code to handle this case. We can then place that code False branch of our conditional statement handling the logic of the program:
p1 = int(input("Enter a positive integer for player 1: "))
p2 = int(input("Enter a positive integer for player 2: "))
p3 = int(input("Enter a positive integer for player 3: "))
if p1 <= 0 or p2 <= 0 or p3 <= 0:
print("Error")
elif p1 == p2 or p2 == p3 or p3 == p1:
print("Tie")
elif p1 % 2 == 0 and p2 % 2 == 0 and p3 % 2 == 0:
if p1 < p2 and p1 < p3:
print("Player 1 wins")
elif p2 < p1 and p2 < p3:
print("Player 2 wins")
else:
print("Player 3 wins")
elif p1 % 2 != 0 and p2 % 2 != 0 and p3 % 2 != 0:
if p1 < p2 and p1 < p3:
print("Player 1 wins")
elif p2 < p1 and p2 < p3:
print("Player 2 wins")
else:
print("Player 3 wins")
else:
if p1 > p2 and p1 > p3:
print("Player 1 wins")
elif p2 > p1 and p2 > p3:
print("Player 2 wins")
else:
print("Player 3 wins")There we go! We’ve written a complete program that implements the problem statement given above. Did you think it would end up being this complex? Sometimes even a simple problem statement ends up requiring quite a bit of code to implement it fully.
Testing - Branch Coverage
The next step is to perform some testing of our program to make sure it is fully working. To do that, we need to come up with a set of inputs that would achieve branch coverage, and possibly even path coverage. However, this time our program is spread across three different sets of conditional statements, so it makes it a bit more difficult to do. So, let’s focus on each individual statement separately and see if we can find a set that work for each of them.
Top-Level Statement
First, we see the top-level statement has 5 branches to cover, so we need to come up with 5 different sets of inputs in order to achieve branch coverage. We can keep the inputs very small, just to make our testing a bit simpler. Here are the 5 branches to cover, and an input that will reach each one:
- Invalid input:
-1, -1, -1 - Tie:
1, 1, 1 - All Even:
2, 4, 6 - All Odd:
1, 3, 5 - Mixed:
1, 2, 3
Notice how we are trying to come up with the simplest possible inputs for each branch? That will make it easier to combine these inputs with the ones used in other conditional statements to find an overall set of inputs that will achieve branch coverage for the entire program.
Smallest Statements
Next, we can look at the code to find the smallest number. This code is used when the inputs are either all even or all odd. So, we know that either inputs 2, 4, 6 or 1, 3, 5 will execute this code.
Within the code itself, we see three branches, depending on which player wins. So, if we start with the input 2, 4, 6, we’ll see that this will execute the branch where player 1 wins. To execute the other branches, we can simply reorder the inputs:
- Player 1 Wins:
2, 4, 6 - Player 2 Wins:
4, 2, 6 - Player 3 Wins:
4, 6, 2
That will achieve branch coverage for the “smallest” conditional statement, and even overlaps with one of the inputs used in the top-level statement.
Largest Statement
The same applies to the conditional statement to find the largest number, but in this case we need a mix of even and odd numbers in the input. So, the input 1, 2, 3 will execute this code, and that input results in player 3 winning. Once again, we can reorder that input a bit to execute all three branches of this code:
- Player 1 Wins:
3, 1, 2 - Player 2 Wins:
1, 3, 2 - Player 3 Wins:
1, 2, 3
Overall Program
Therefore, based on our analysis, we can achieve branch coverage across the entire program using 9 different inputs:
- Invalid input:
-1, -1, -1 - Tie:
1, 1, 1 - All Even:
- Player 1 Wins:
2, 4, 6 - Player 2 Wins:
4, 2, 6 - Player 3 Wins:
4, 6, 2
- Player 1 Wins:
- All Odd:
1, 3, 5 - Mixed:
- Player 1 Wins:
3, 1, 2 - Player 2 Wins:
1, 3, 2 - Player 3 Wins:
1, 2, 3
- Player 1 Wins:
This will execute each branch of all conditional statements in the program at least once.
Path Coverage
Once we’ve achieved branch coverage, we should also quickly look at path coverage: is there any possible pathway through this program that we haven’t tested yet? As it turns out, there are two, but they are somewhat difficult to find. Can you spot them? See if you can figure it out before continuing on in this page.
The paths we missed are situations where the numbers are all odd, but a player other than player 1 wins. While we tested all possible branches in the “smallest” conditional statement, we didn’t test it using all odd numbers more than once. So, to truly achieve path coverage, we should add two more inputs to our list above:
- Invalid input:
-1, -1, -1 - Tie:
1, 1, 1 - All Even:
- Player 1 Wins:
2, 4, 6 - Player 2 Wins:
4, 2, 6 - Player 3 Wins:
4, 6, 2
- Player 1 Wins:
- All Odd:
- Player 1 Wins:
1, 3, 5 - Player 2 Wins:
3, 1, 5 - Player 3 Wins:
3, 5, 1
- Player 1 Wins:
- Mixed:
- Player 1 Wins:
3, 1, 2 - Player 2 Wins:
1, 3, 2 - Player 3 Wins:
1, 2, 3
- Player 1 Wins:
So, with a total of 11 inputs, we can finally say we’ve achieved both branch coverage and path coverage of this program.
Subsections of Worked Example
Nesting Practice
Let’s try some simple practice problems. These problems are not graded - they are just for you to practice before doing the real exercises in the lab itself. You can find the answers below each question by clicking the button below each question.
4.11 Reading Code
Consider the following Python program:
p1 = int(input("Enter a positive integer for player 1: "))
p2 = int(input("Enter a positive integer for player 2: "))
p3 = int(input("Enter a positive integer for player 3: "))
if p1 <= 0 or p2 <= 0 or p3 <= 0:
print("Error")
else:
twos = (p1 + p2 + p3) // 2
threes = (p1 + p2 + p3) // 3
fours = (p1 + p2 + p3) // 4
if p1 == p2 or p2 == p3 or p3 == p1:
print("Tie")
elif p1 != twos and p2 != threes and p3 != fours:
print("Draw")
else:
if p1 == twos:
print("Player 1 Wins")
if p2 == threes:
print("Player 2 Wins")
if p3 == fours:
print("Player 3 Wins")Explain, in your own words, a set of rules for the game that this program is simulating.
A fully correct answer is a succinct set of rules for the game and what leads to the various outcomes. A partially correct answer is a step-by-step description of each line in the program and the output it will produce based on the input.
Hint: it is possible for multiple players to win a round in this game.
4.12 Testing Code
Consider the Python program in the question above. Give a set of inputs that will achieve branch coverage for this program. You do not have to achieve path coverage!
Hint: try 3, 2, 1 as one possible input. What branches will that execute?
4.13 Writing Code
Write a complete Python program that meets the specification below.
A childcare supervisor has developed a set of rules to determine if children under their care may play indoors or outdoors. Here are the rules:
- If it is raining, then the children must play indoors since they’ll get wet. This rule takes precedence over all other rules.
- If the temperature is below 0° C, then the children must play indoors because it is too cold, unless there is snow on the ground. In that case, children may play both indoors and outdoors.
- If the temperature is above 40° C, then the children must play indoors because it is too hot, unless the pool is open. In that case, children may play both indoors and outdoors.
- If the temperature is between 20° C and 30° C, then the children must play outdoors because it is a nice day.
- Otherwise, if no other rules are matched, children may choose to play both indoors and outdoors.
Write a program that will help determine if the children may play indoors, outdoors, or both. The program will prompt the user for four inputs in the following order:
- The temperature as an integer (measured in degrees Celsius).
- Whether it is raining:
yesorno. - Whether there is snow on the ground:
yesorno. - Whether the pool is open:
yesorno.
The program should output either indoors, outdoors, or both, depending on the rules described above. Your program must make use of chained and/or nested conditional statements.
Hint: after reading input, the yes and no answers can be converted to Boolean values once and stored in Boolean variables. This will simplify the Boolean expressions used in the conditional statements.
Summary
In this lab, we introduced several major important topics in Python. Let’s quickly review them.
Booleans in Python
TrueFalsebool()procedure to convert values- If the input is the value
False, the value0, the valueNone, or anything with 0 length, including the empty string, it will returnFalse. - Otherwise, for all other values it will return
True.
- If the input is the value
Boolean Operators
andornot
Boolean Comparators
==equal!=not equal<less than<=less than or equal to>greater than>=greater than or equal to
Comparators and Strings
Strings are compared using lexicographic order
Boolean Order of Operations
- Math operators (following their order of operations)
- Boolean comparators
notandor
Conditional Statements
- if statement
if <boolean expression>:
<block of statements>- if-else statement
if <boolean expression>:
<block of statements 1>
else:
<block of statements 2>Testing
- Branch Coverage - all possible branches are executed at least once
- Path Coverage - all possible paths through branches are executed at least once
- Edge Cases - values that are near the point where Boolean expressions go from
FalsetoTrue
Mutually Exclusive
Conditional statements are mutually exclusive when only one of the many branches will be executed for any possible input.
Chained Conditionals
if condition_1:
print("1")
else:
if condition_2:
print("2")
else:
if condition_3:
print("3")
else:
print("4")is equivalent to:
if condition_1:
print("1")
elif condition_2:
print("2")
elif condition_3:
print("3")
else:
print("4")Nested Conditionals
if condition_1:
if condition_2:
print("1 and 2")
elif condition_3:
print("1 and 3")
else:
print("1 and not 2 or 3")
elif condition_4:
if condition_2:
print("4 and 2")
elif condition_3:
print("4 and 3")
else:
print("4 and not 2 or 3")
else:
print("neither 1 nor 4")Variable Scope
Variable scope refers to what parts of the code a particular variable is accessible in. Python uses function scope, which means that a variable defined anywhere in a function is available below that definition in any part of the same function.
Other languages use block scope, where variables are only available within the block where they are defined.