Subsections of Loops
Introduction
YouTube VideoResources
Over the last few labs, we’ve explored how we can change the control flow of our programs using conditional statements. A program that doesn’t contain any conditional statements will have a linear control flow. Each time we run the program, it will execute the same steps in the same order, but it may use different data based on input from the user.
When a program contains a conditional statement, its control flow can split into different branches. This means that each program execution may take a different path through the program, but it will eventually reach the end. There is no way to go back and repeat a step that has already been done!
In this lab, we’re going to introduce the other important method for modifying the control flow of our programs - a loop or iteration statement. In programming, a loop is a construct that allows us to repeatedly execute the same piece of code, either for a set number of times, or while a particular Boolean condition is true. Each time we execute the code inside the loop, we call that an iteration of the loop.
Loops are one of the most useful ways we can modify the control flow in our programs. With both loops and conditional statements in our list of available programming skills, we can write programs that execute different branches of code based on a Boolean expression, and we can also repeatedly execute the same piece of code either a defined number of times or while a Boolean expression evaluates to True. This allows us to build some truly useful programs.
In this lab, we’re going to explore ways to use loops in Python. Python supports two different types of loops, while loops and for loops, both of which can be used in a variety of different ways in our programs. We’ll also explore how to use these loops to receive input from the user and handle the case where a user provides invalid input, and finally we’ll look at some ways to test our code containing loops to confirm that they are working correctly and won’t cause issues.
Let’s get started!
Subsections of Introduction
While Loops
YouTube VideoResources
The first type of loop to explore in Python is the while loop. A while loop uses a Boolean expression, and will repeat the code inside of the loop as long as the Boolean expression evaluates to True. These loops are typically used when we want to repeat some steps, but we aren’t sure exactly how many times it must be done. Instead, we typically know that there is some condition that must be True while we repeat the code, and once it turns False we can stop looping and continue with the program.
The general syntax for a while loop in Python is shown here:
while <boolean expression>:
<block of statements>Notice that this syntax is very similar to an if statement. We start with the keyword while, followed by some sort of a <boolean expression> that will evaluate to either True or False. The Boolean expression in Python does not need to be placed inside of parentheses. After the Boolean expression is a single colon :. Then, starting on the next line and indented one level is a <block of statements> that will be executed when the Boolean expression evaluates to True. Once again, just like in an if statement, we know which statements are part of the block within a while loop based solely on indentation.
It is possible for the Boolean expression to evaluate to False initially, which will bypass the loop entirely and never execute the code inside of it. Likewise, if we aren’t careful, we can also write a loop where the Boolean expression will always be True, and the loop will run infinitely, causing our program to lock up and never terminate.
Code Tracing Example
To truly understand how a while loop works in Python, let’s go through a simple code tracing example in Python Tutor. Consider the following Python program:
x = int(input("Enter a number from 0 to 100: "))
total = 0
while total % 100 != x:
total = total + 9
print(f"The smallest multiple of 9 that ends in {x} is {total}")See if you can figure out what this program does before moving on!
As always, you can copy and paste this code into Python Tutor, or click this Python Tutor link.
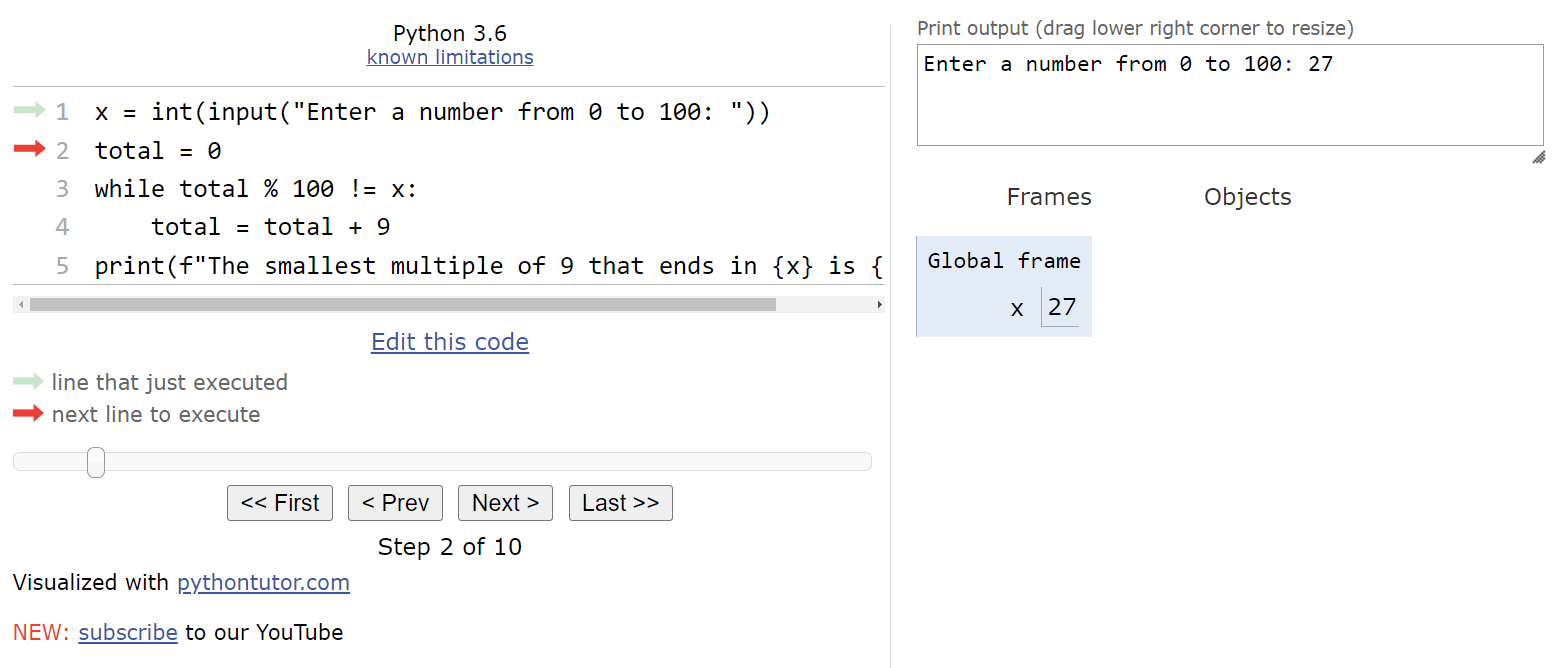
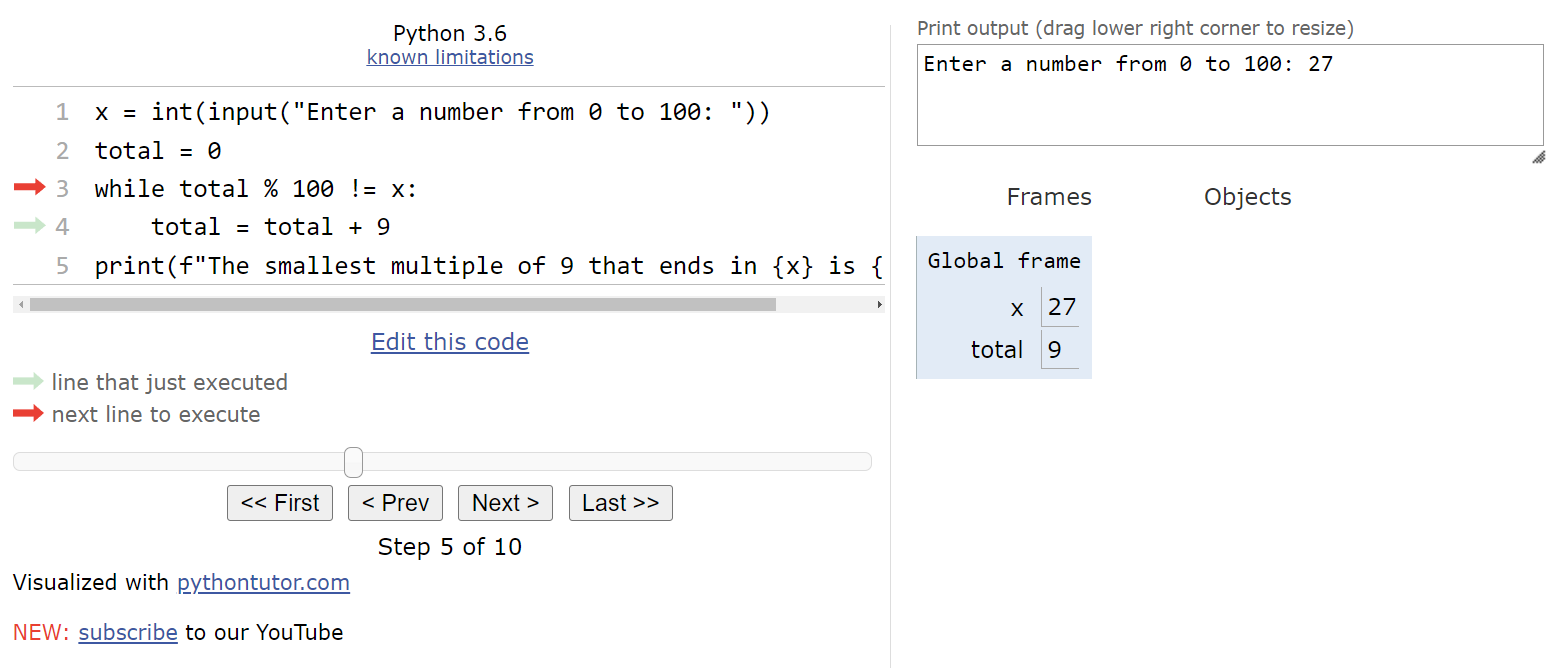
When we load this code in Python Tutor, we should see the usual default state. The first line of the program will prompt the user for input and store it in the variable x.
For this example, let’s assume the user inputs the string "27".
Therefore, we’ll store the value
$ 27 $ in the variable x.
The next line will store the value
$ 0 $ in the variable total, as shown here:
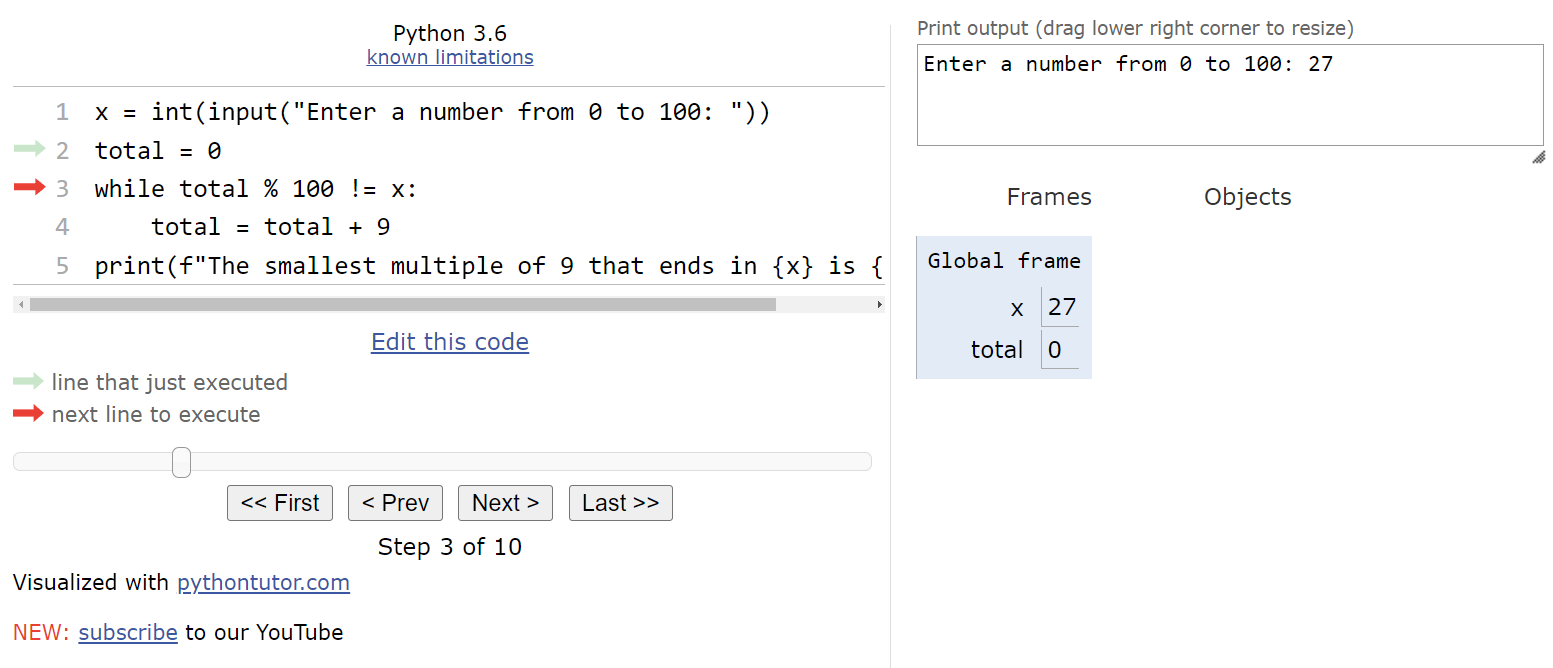
At this point, we’ve reached the beginning of the while loop. So, we’ll need to determine if the Boolean expression evaluates to True or False. In this case, the value of total % 100 is equal to
$ 0 $, so it is not equal to the value stored in x. Therefore, the Boolean expression is True, and we should enter the loop.
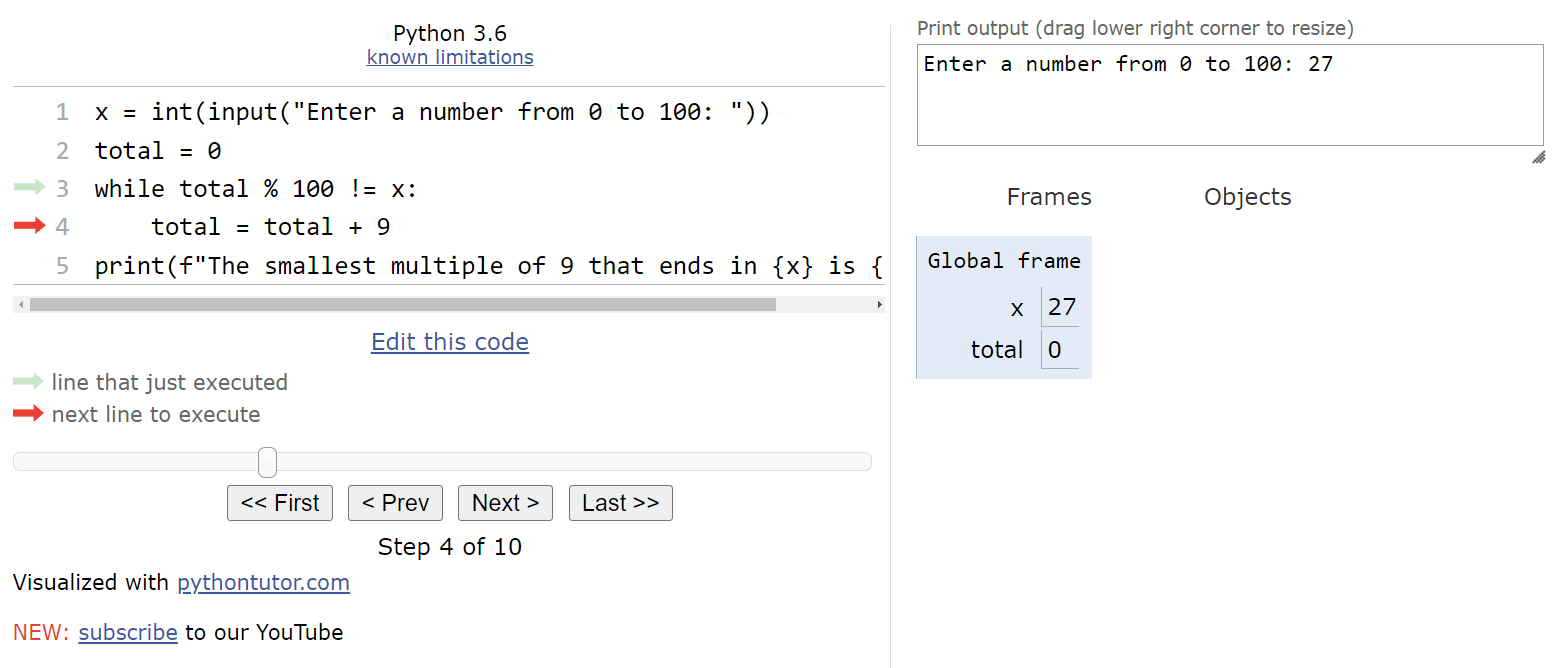
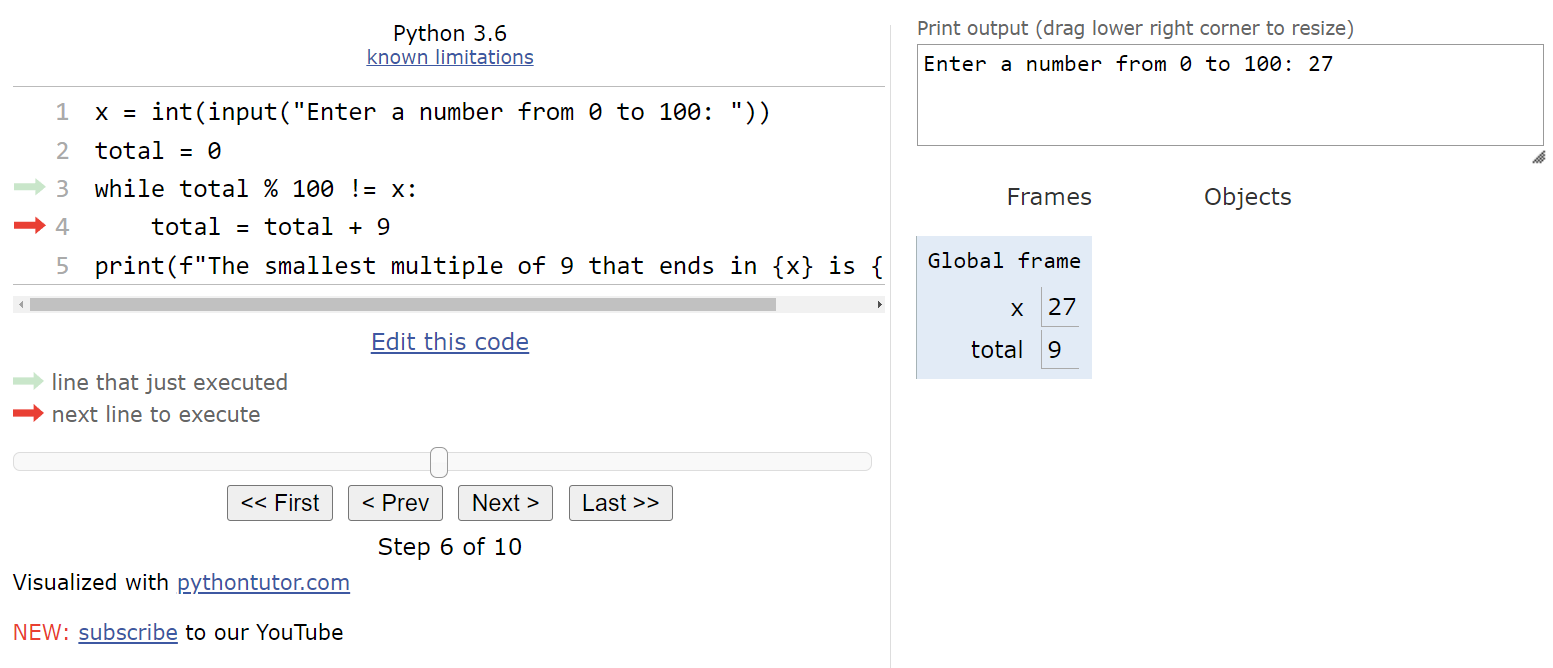
Inside of the loop, we are simply adding
$ 9 $ to the value in total. So, we’ll see that variable is updated, and the execution pointer goes back to the top of the loop.
Now that we are back at the top of the loop, we need to check the Boolean expression again. This time the value of total % 100 is
$ 9 $, which still isn’t equal to the value stored in x, so we’ll enter the loop again.
We’ll add
$ 9 $ to the total here, and jump to the top again.
Once again, we will check the Boolean expression and see that it is still True, so we’ll enter the loop and add
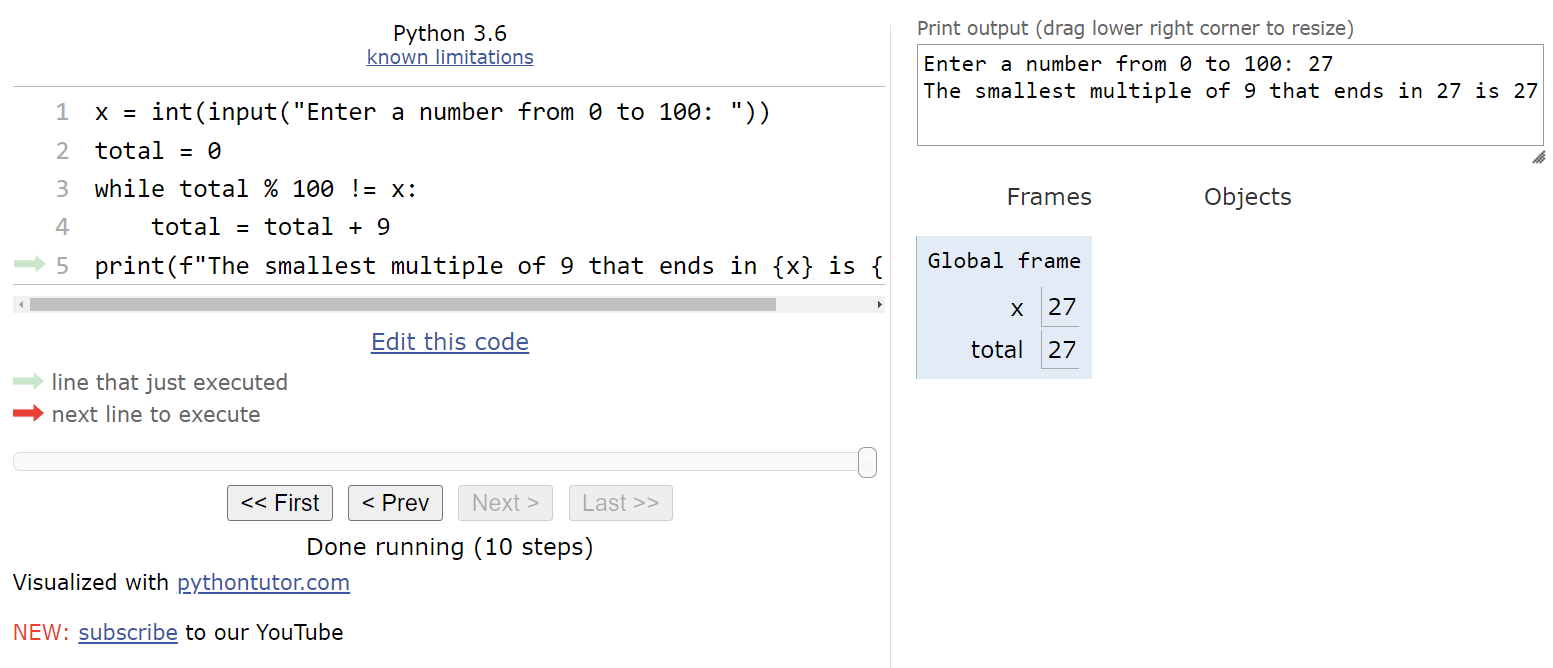
$ 9 $ to the total yet again before repeating the process from the top of the loop. At this point, we should see this state in Python tutor.
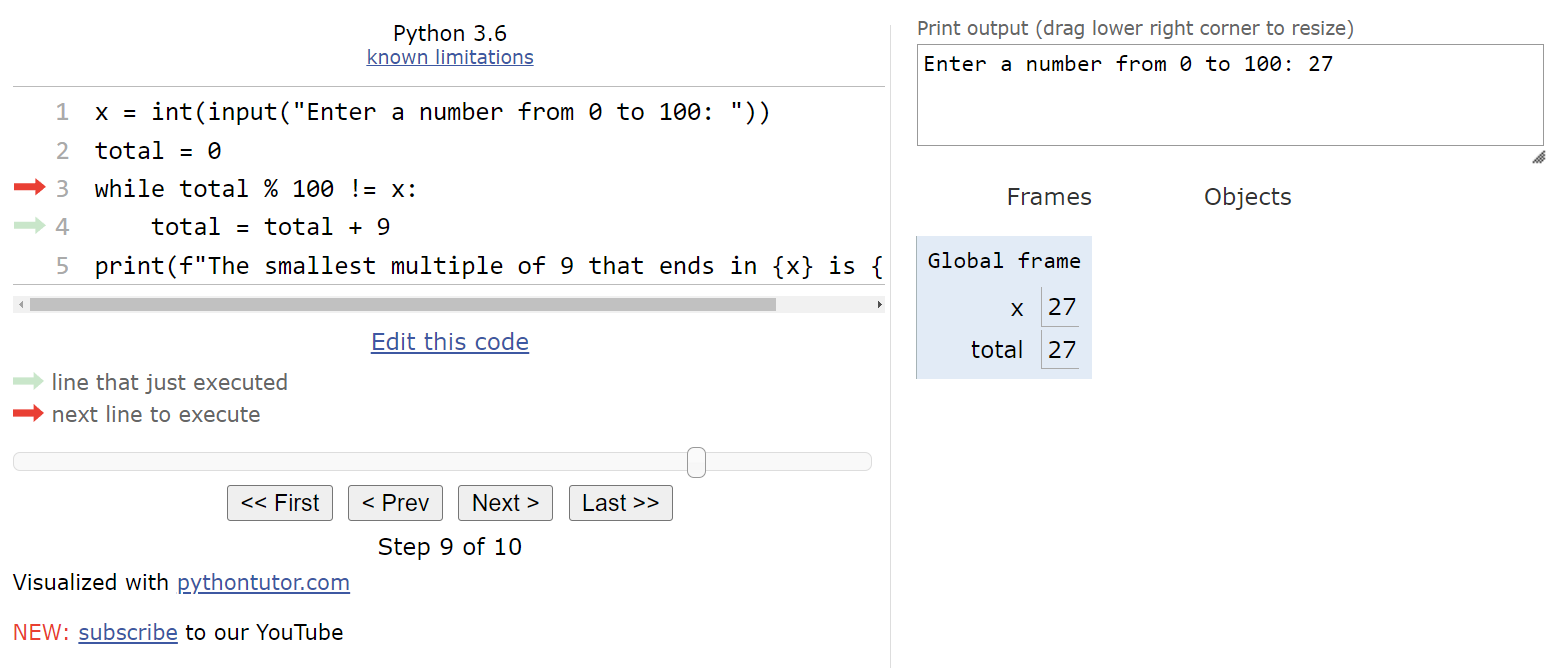
When we compute total % 100, we get the value
$ 27 $, which is the same as the value stored in x. This will make the Boolean expression evaluate to False, so we can skip the loop and jump to the bottom of the program.
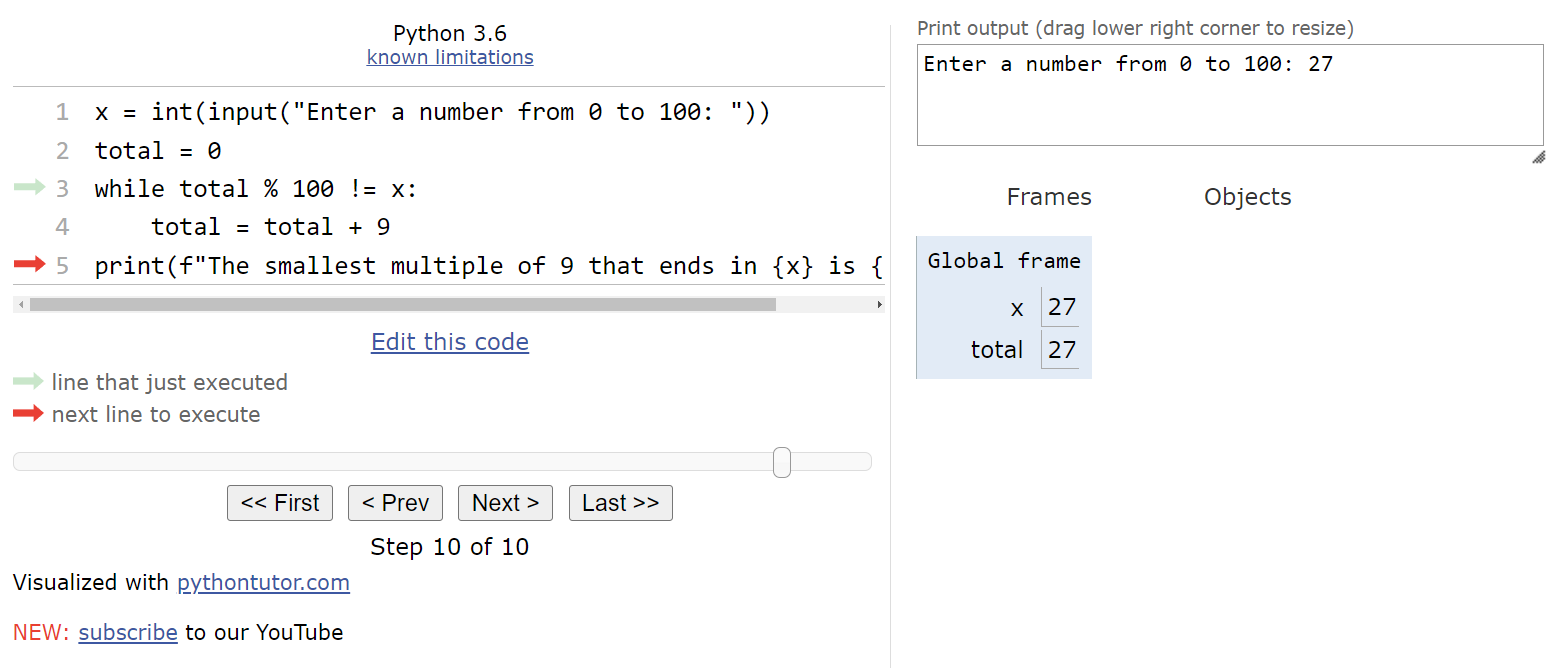
Here, we are simply printing out the output, and then the program will terminate.
A full animation of this program’s execution in Python Tutor is shown here.
Tracing the execution of a while loop is quite simple, especially with tools such as Python Tutor to help us make sure we’re updating the variables in the correct order.
Subsections of While Loops
For Loops
YouTube VideoResources
Python also includes a second type of loop that is very useful, the for loop. A for loop is used when we want to repeat the steps a certain number of times. However, in Python, we can’t just say that we want to repeat something
$ 10 $ times. Instead, we use the built-in range() function in Python to generate a list of numbers that we use in our loop. Then, our for loop will repeat once for each number in the list, and we can even access that number using an iterator variable
We’ll learn more about lists in Python in a later lab. For now, we’re just going to use the range() function to generate them for use with for loops.
Range Function
The range() function can be used in three different ways, depending on the number of arguments given when calling the function:
range(stop)- with a single argument, therange()function will generate a list of numbers that begins at $ 0 $ and stops before it reaches thestopvalue. For example,range(10)will generate a list of numbers from $ 0 $ through $ 9 $. This is great, since there will be $ 10 $ numbers in total, so a for loop usingrange(10)will repeat $ 10 $ times.range(start, stop)- with two arguments, therange()function will generate a list of numbers that begins atstartand stops before it reaches thestopvalue. So,range(3,8)will generate the list[3, 4, 5, 6, 7]. There will bestop - startnumbers in the range.range(start, stop, step)- with three arguments, therange()function will generate a list of numbers that begins atstart, increases bystepeach time, and stops before thestopvalue. Therefore,range(0, 10, 2)will generate the list[0, 2, 4, 6, 8]. We can also use a negative value forstepto count backwards. So,range(5, 0, -1)will generate the list[5, 4, 3, 2, 1].
You can read more about the Python range() function in the Python Documentation
For Loops
The general structure of a for loop in Python is shown here:
for <iterator variable> in <list>:
<block of statements>The first time we reach a for loop, we’ll keep track of the <list> that we’ll be iterating over. In general, once you start repeating in a for loop, the <list> cannot be changed.
If the list contains at least one item, then we’ll store the first item in the list in the <iterator variable> and enter the for loop to execute the code in the <block of statements> When we reach the end of the block, we’ll jump back to the top and check to see if the <list> contains another item. If so, we’ll store that item in the <iterator variable> and execute the code in the <block of statements> again.
This process will repeat until we’ve used every item in the <list>. Then, we’ll jump to the end of the for loop and continue the program from there.
Code Tracing Example
To really see how a for loop works in Python, let’s use Python Tutor to trace through a quick sample program. Consider this Python program:
x = int(input("Enter a number: "))
line = ""
for i in range(x):
line = line + "*"
print(line)Before working through the code in Python Tutor, see if you can determine what this program does just by reading it!
To step through the code, we can load it into Python Tutor by copy and pasting it there, or by clicking this Python Tutor link.
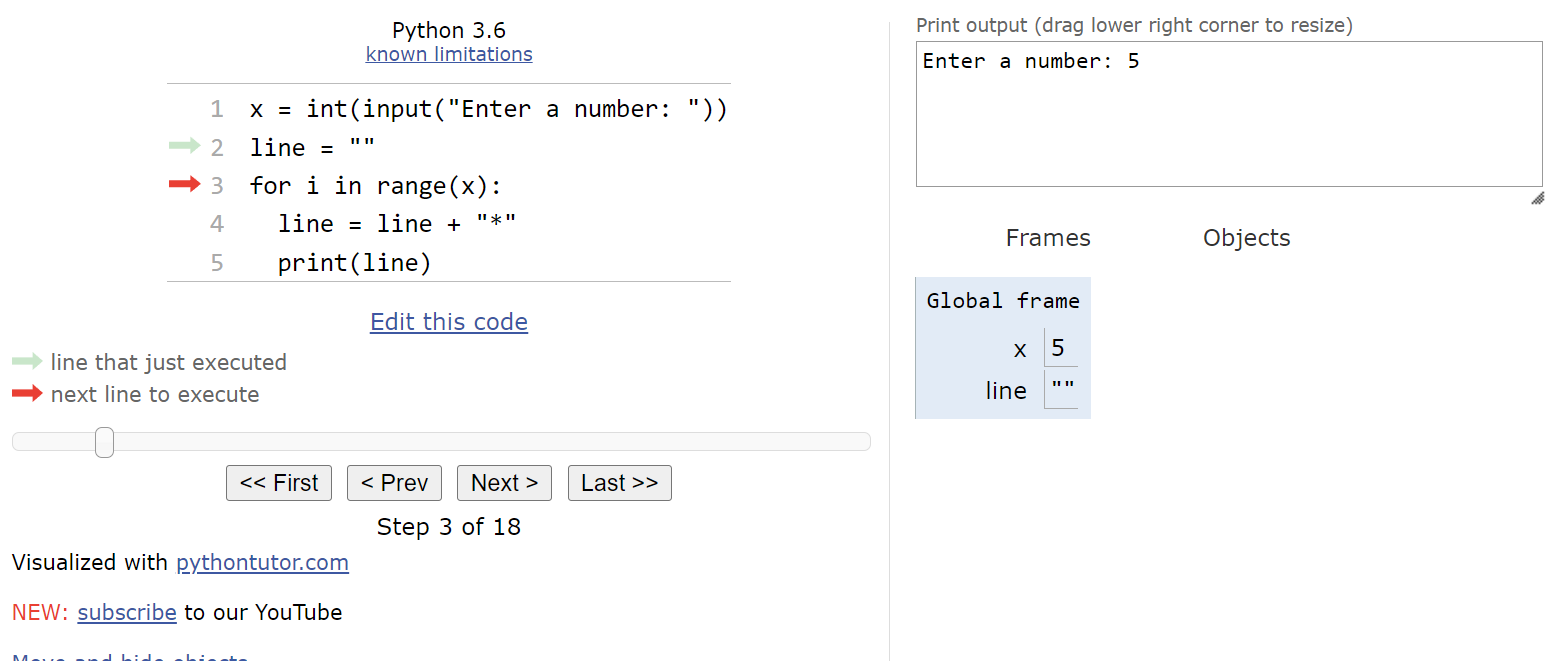
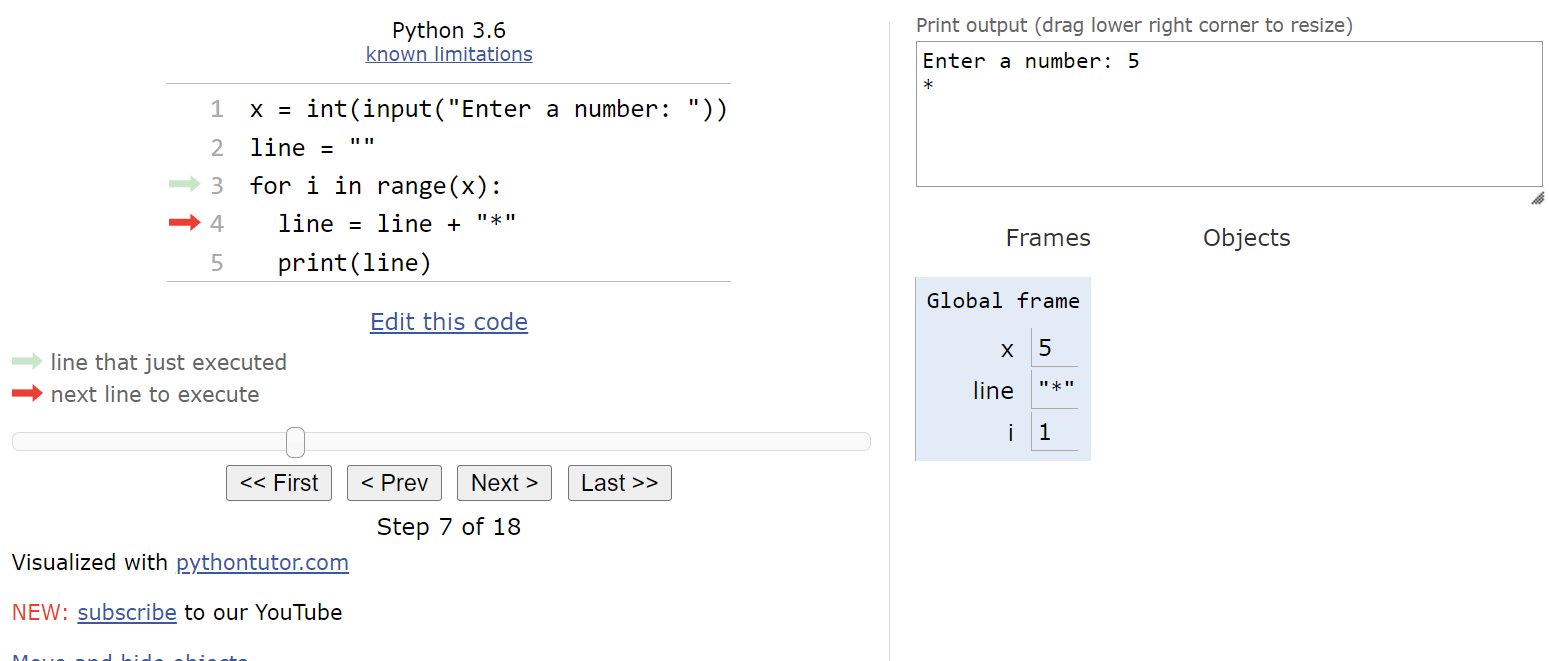
We’ll start with the usual default state as shown here. The first line will read the input from the user.
For this example, let’s assume the user inputs the string "5":
This means that we’ll store the number
$ 5 $ in the variable x. The program will also create an empty string value in the line variable, which we’ll use to generate output.
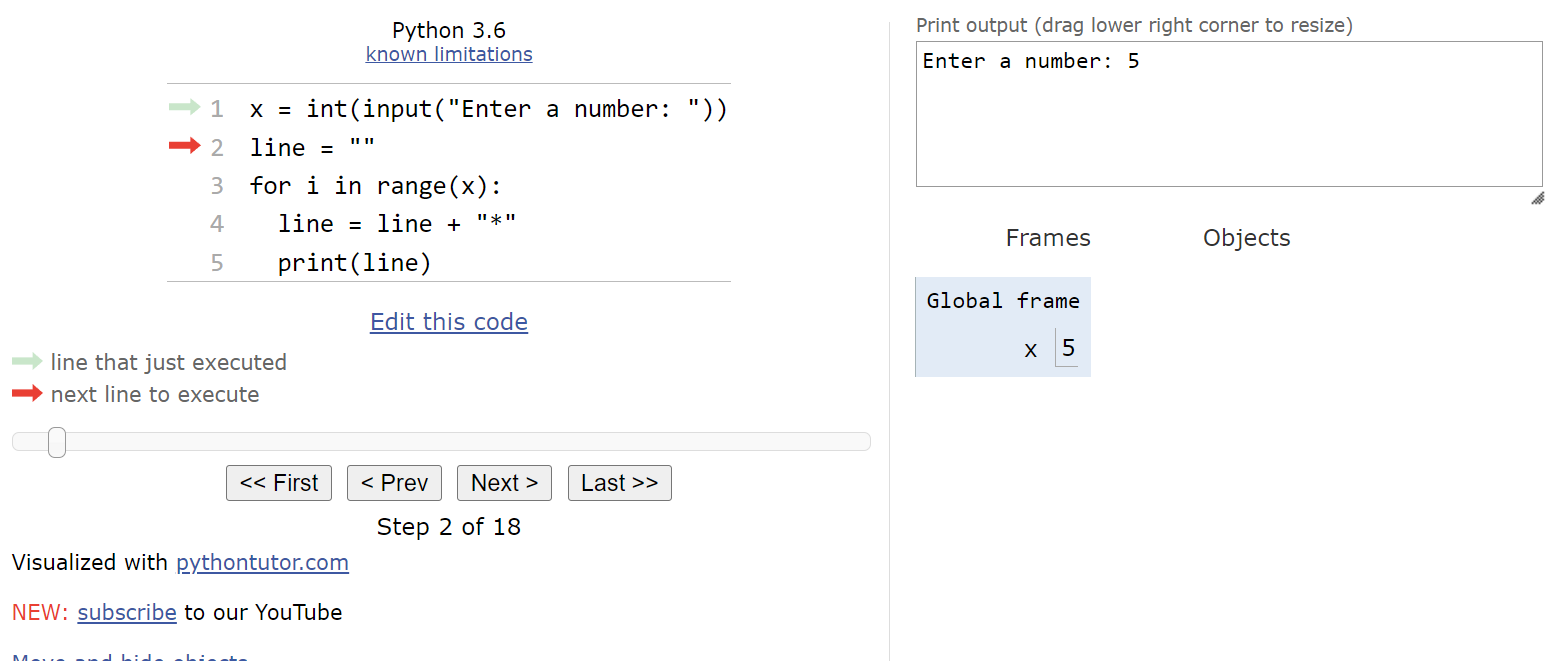
At this point, we should have reached the beginning of the for loop.
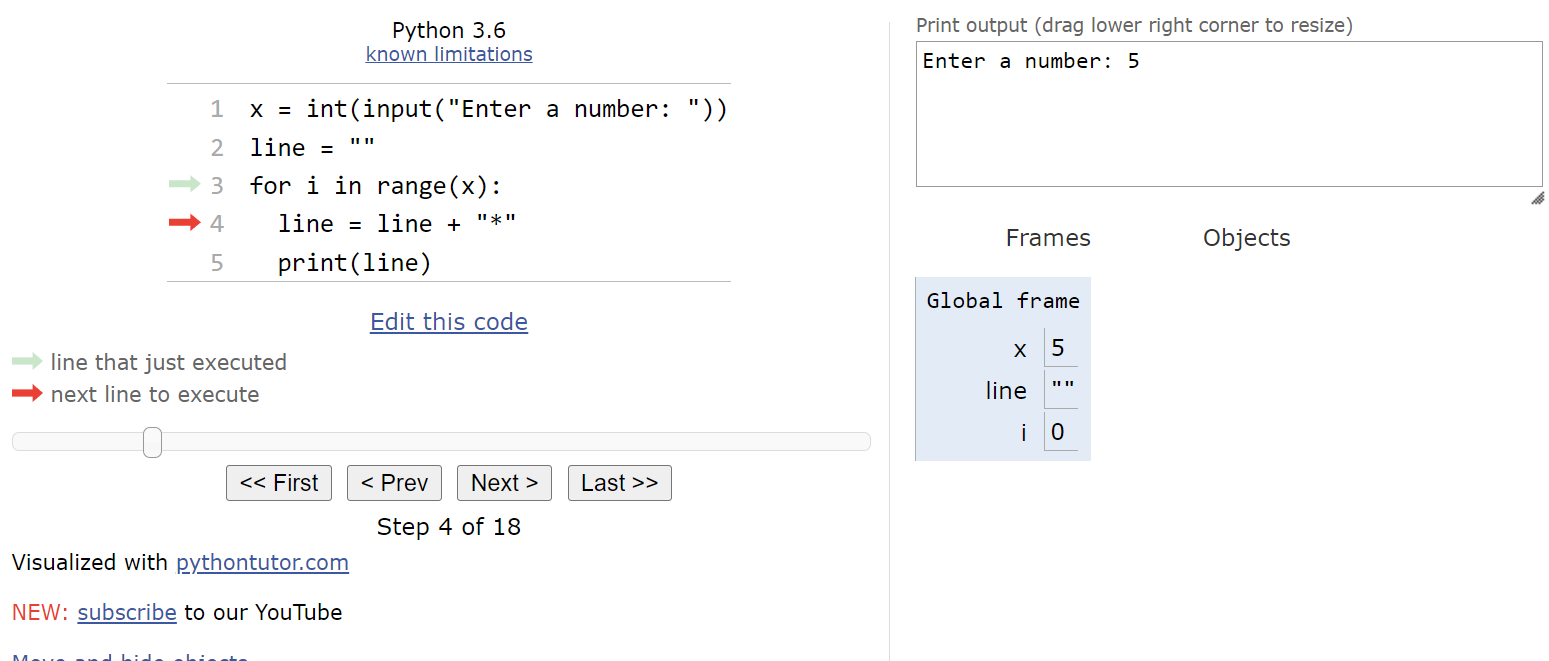
Behind the scenes, Python will generate a list of numbers based on the range() function. Since the range() function is called with a single argument, we know it will be a list of numbers starting at
$ 0 $ and ending before it reaches the value in x, which is
$ 5 $. So, the list will contain the numbers [0, 1, 2, 3, 4], and it will cause the for loop to repeat
$ 5 $ times. For the first iteration of the loop, Python will store the first number in the list,
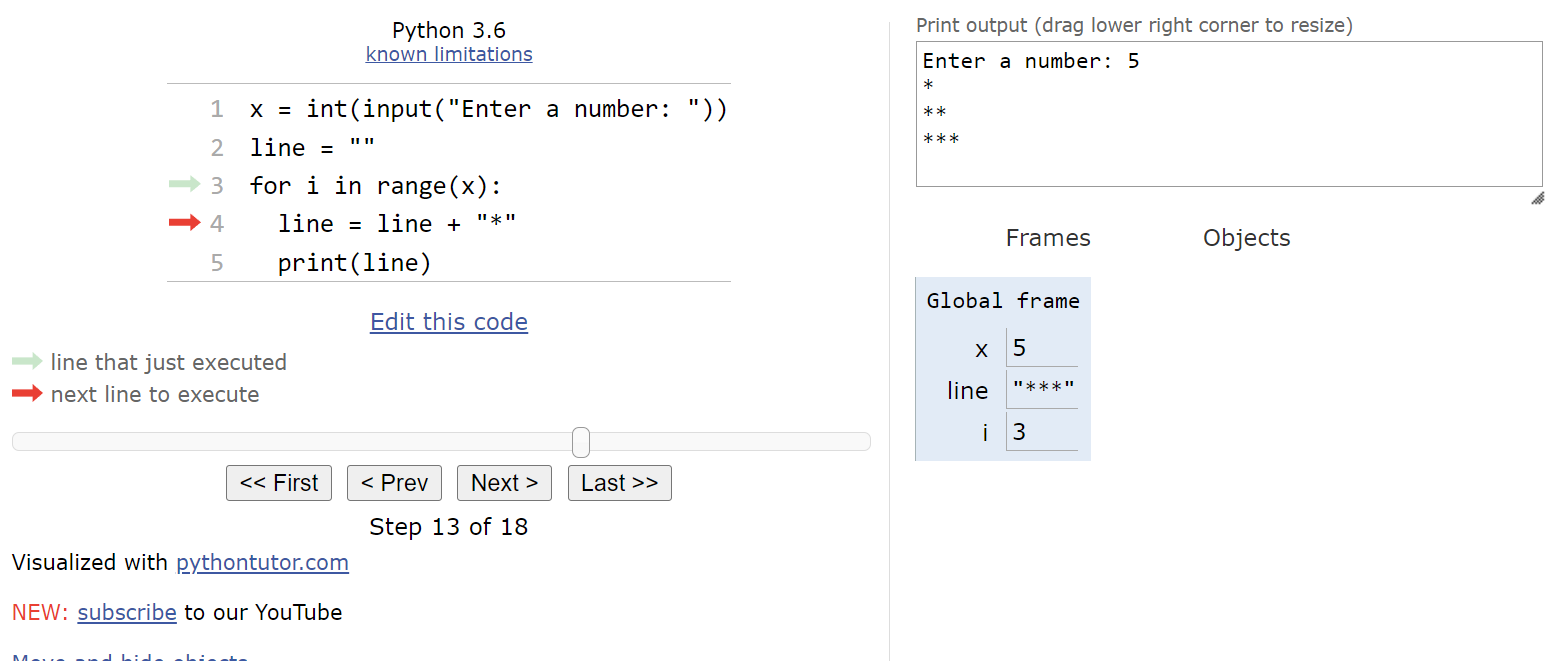
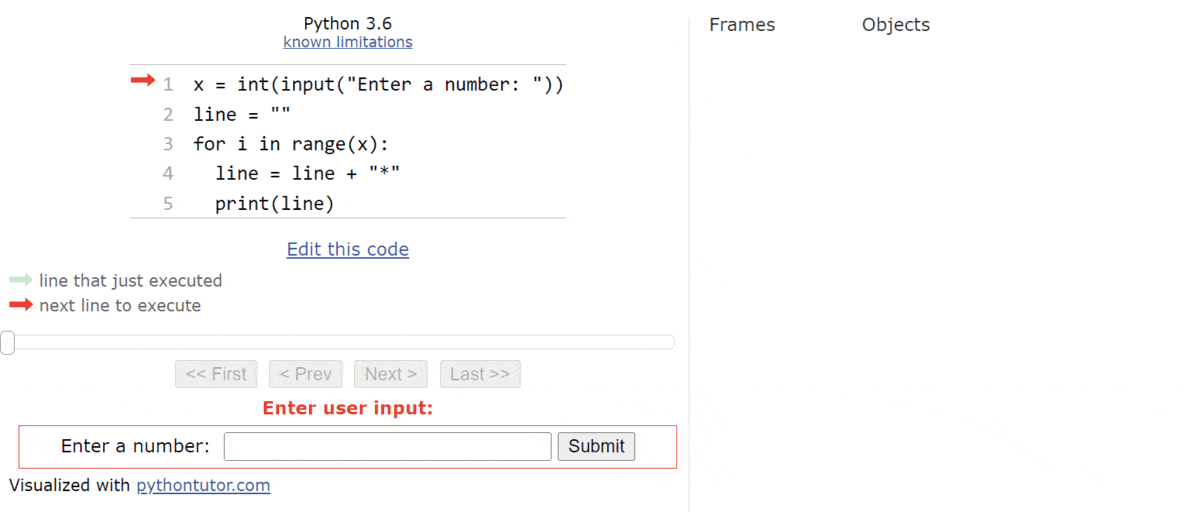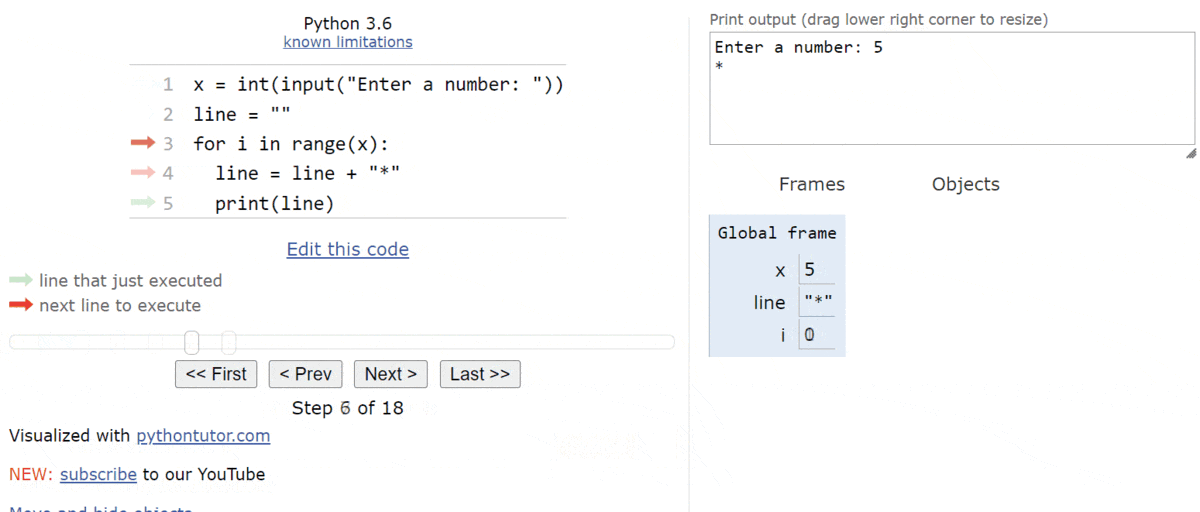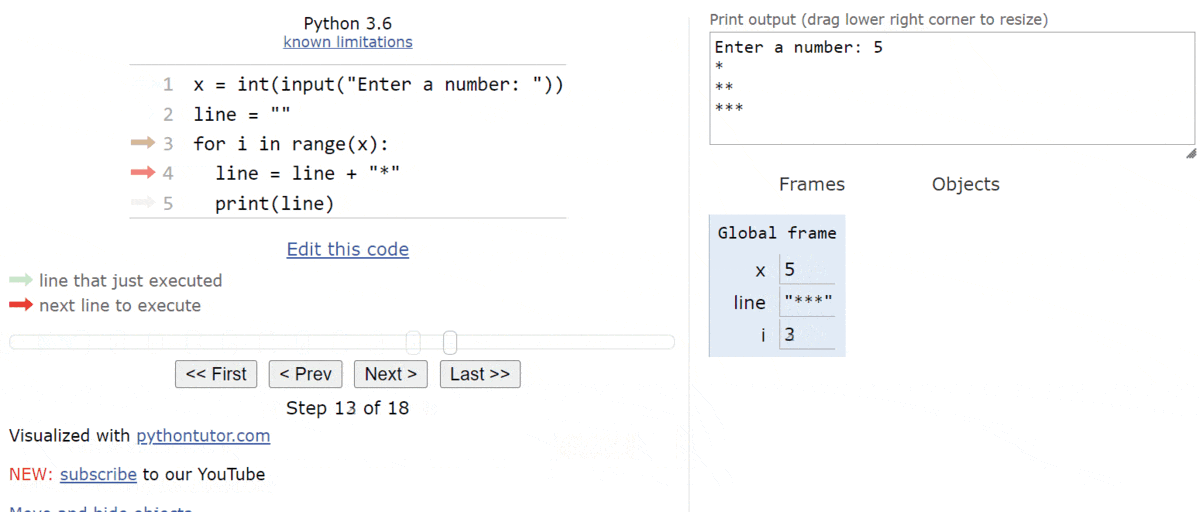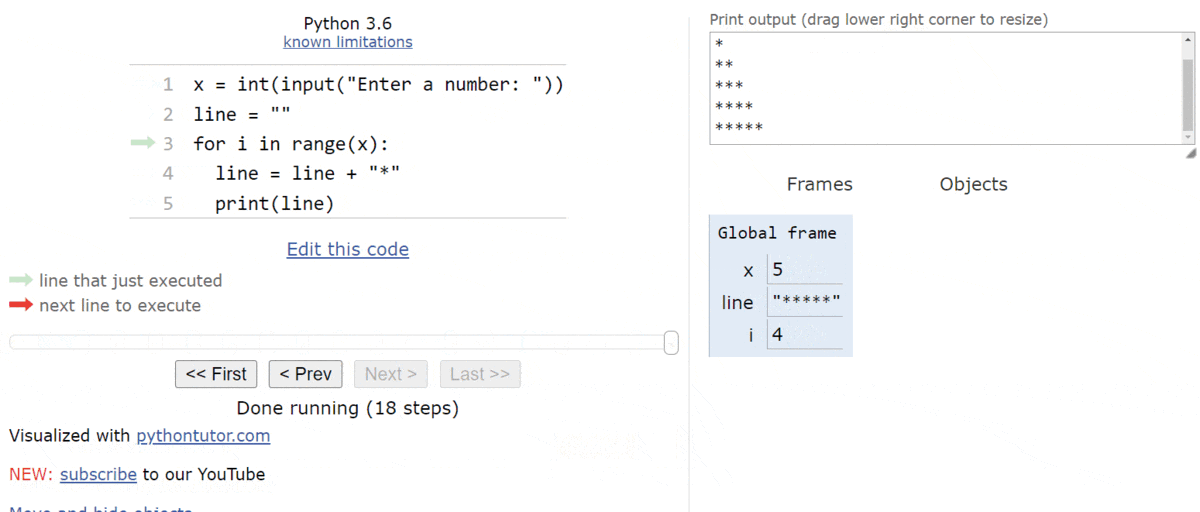
$ 0 $, in the iterator variable i. In programming, we typically use the variable name i to represent our iterator variable. So, once the program has entered the loop, we should see this state:
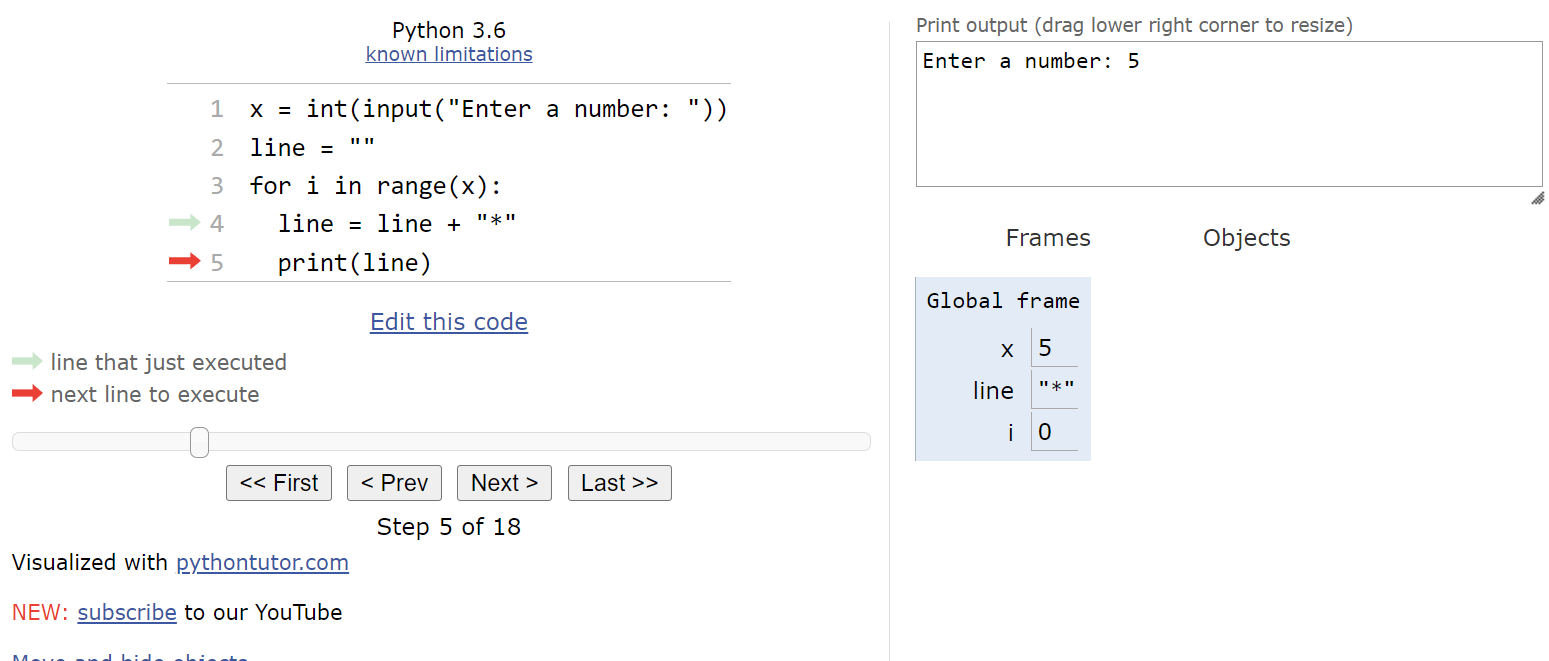
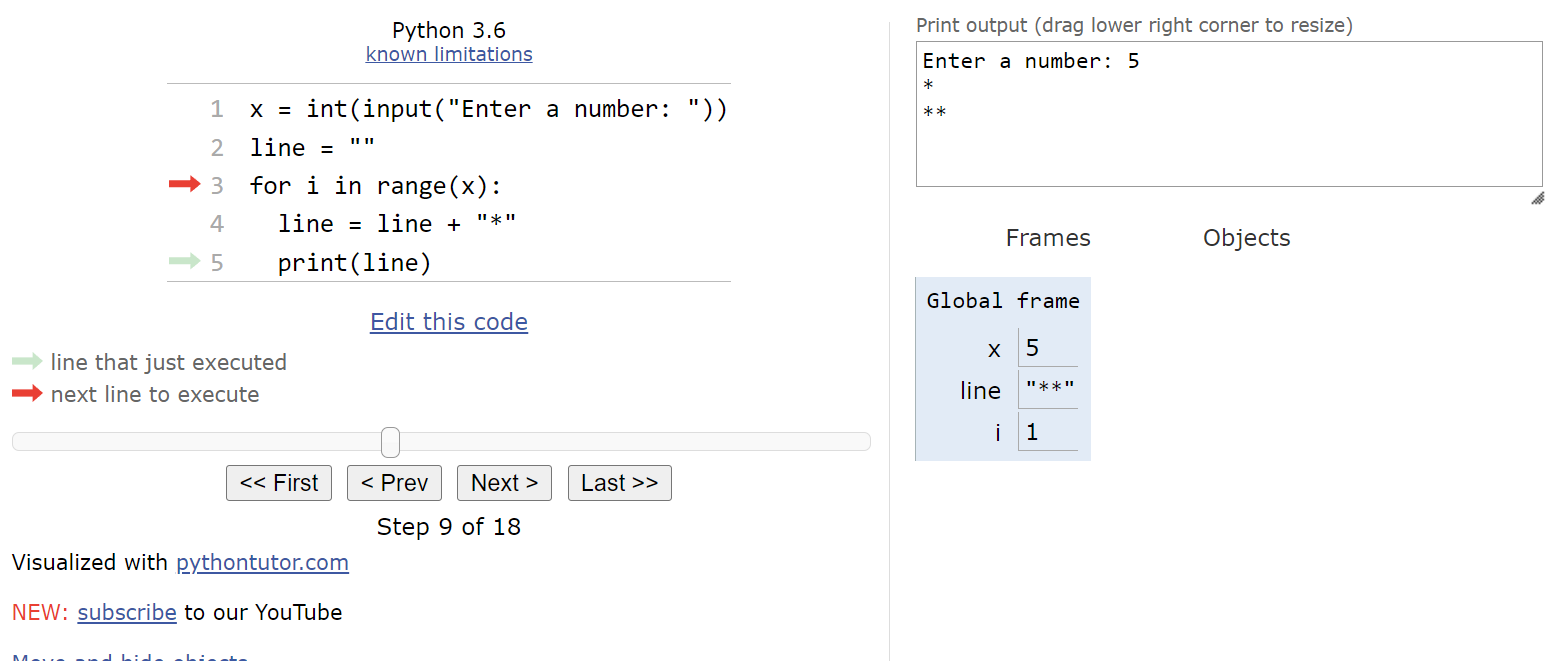
Inside of the loop, the first statement will update the line value by adding an asterisk * to the end of the string. So, after this statement is executed, the line variable will store a string containing a single asterisk.
The second statement will print the line variable to the output.
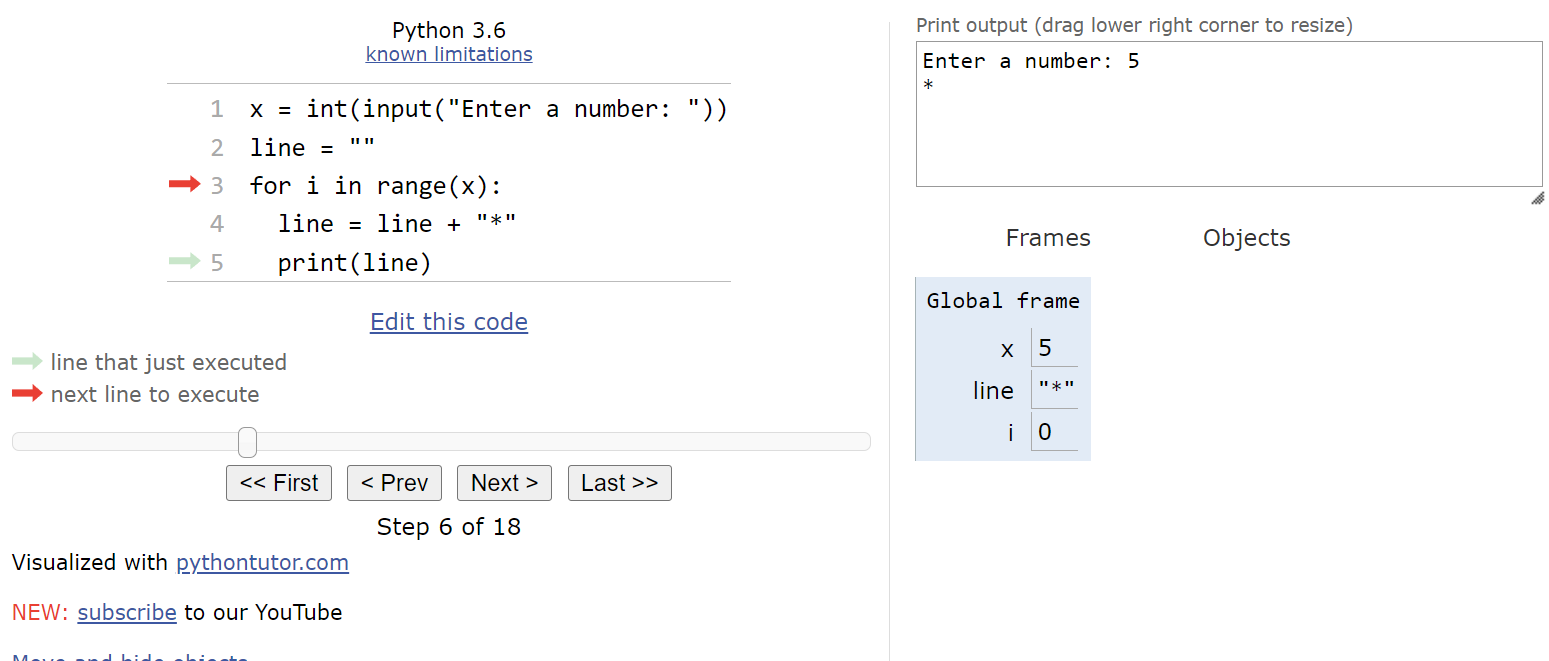
At this point, we’ve reached the end of the for loop, so our execution pointer jumps back up to the top of the loop. Then, we check to see if the list we are iterating through contains more values. Again, this list isn’t shown in Python tutor, so we have to mentally keep track, but we can see the current value in i, and we know what the list contains by looking at the range() function. So, we’ll update i to store the value
$ 1 $, and repeat the loop once again.
Just like before, this iteration will add an asterisk to the string in the line variable, and then print that to the output before repeating once again.
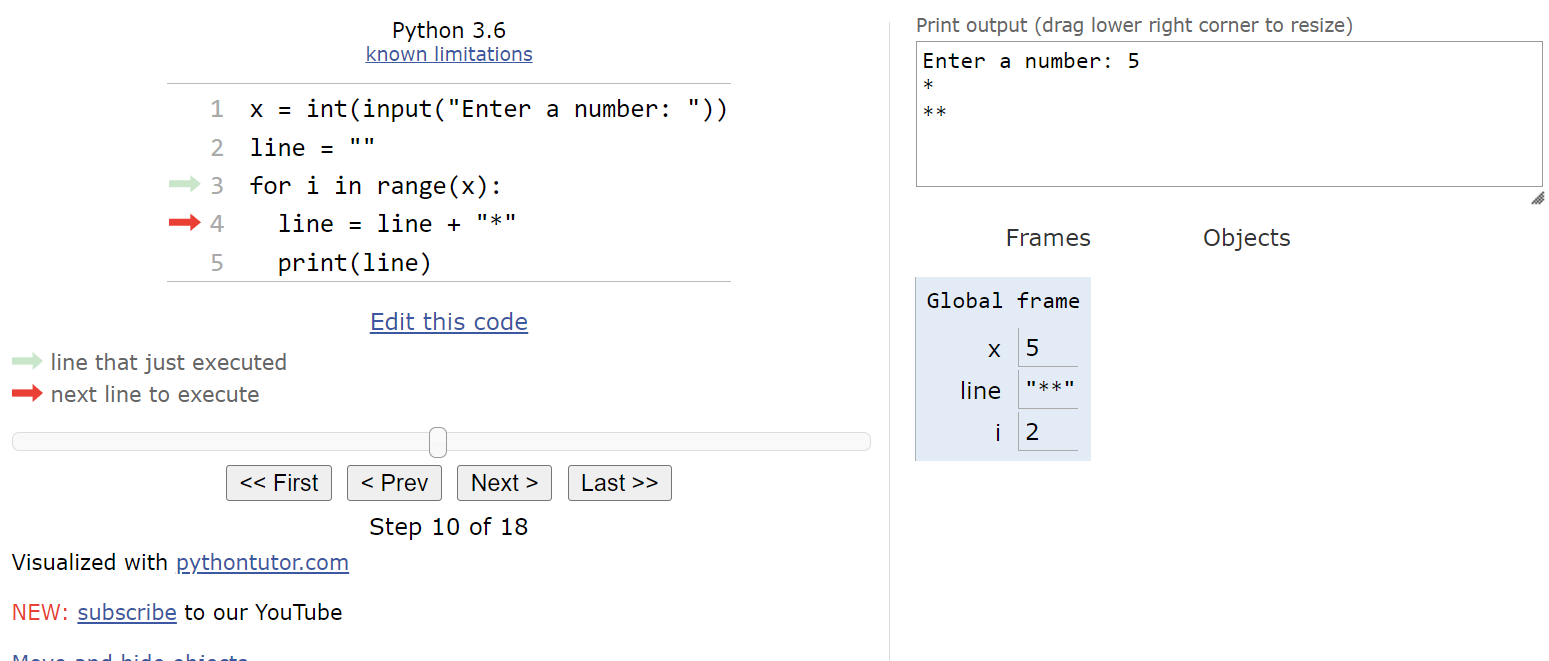
There are still more items in the list, so we’ll update i to the value
$ 2 $ and enter the loop:
In the loop, we’ll update line to contain one more asterisk, and then print it before looping back to the top.
The list still isn’t empty, so we’ll update i to be
$ 3 $ this time:
And then we’ll update line and print it.
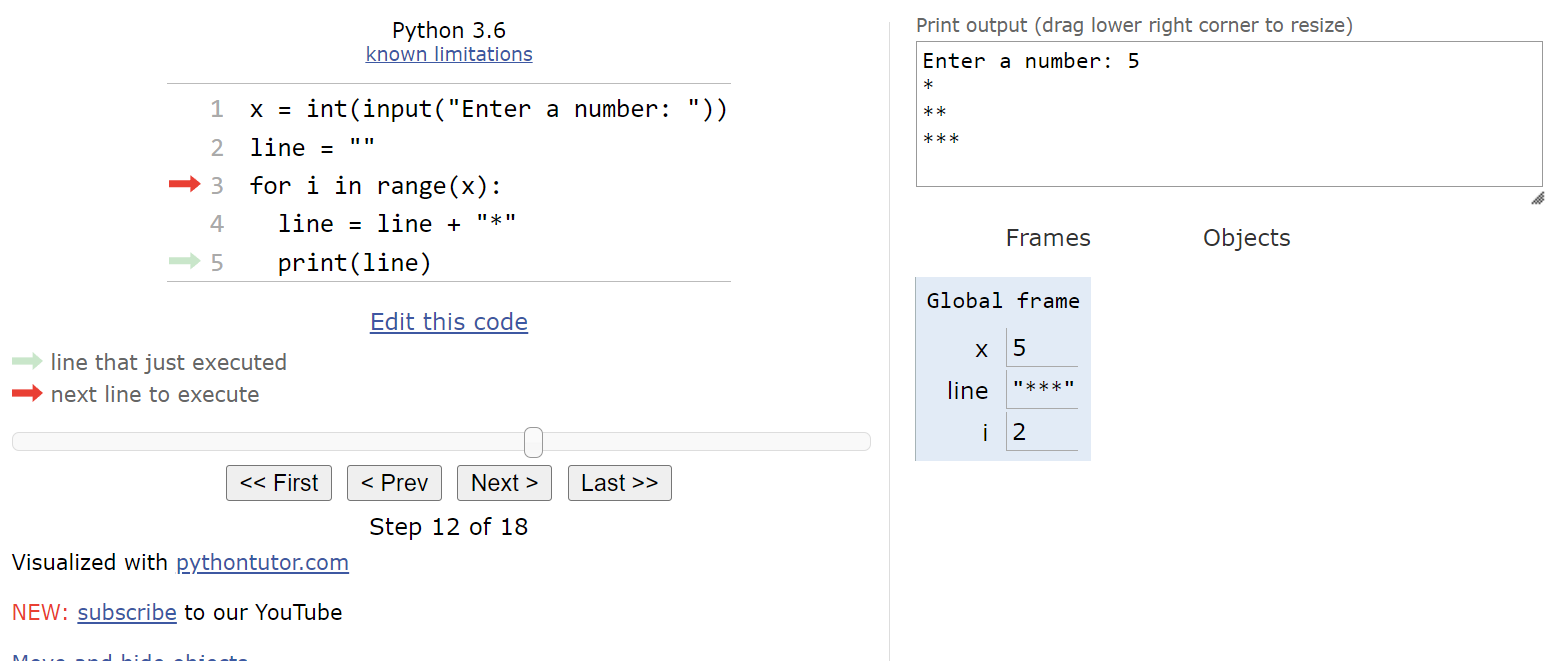
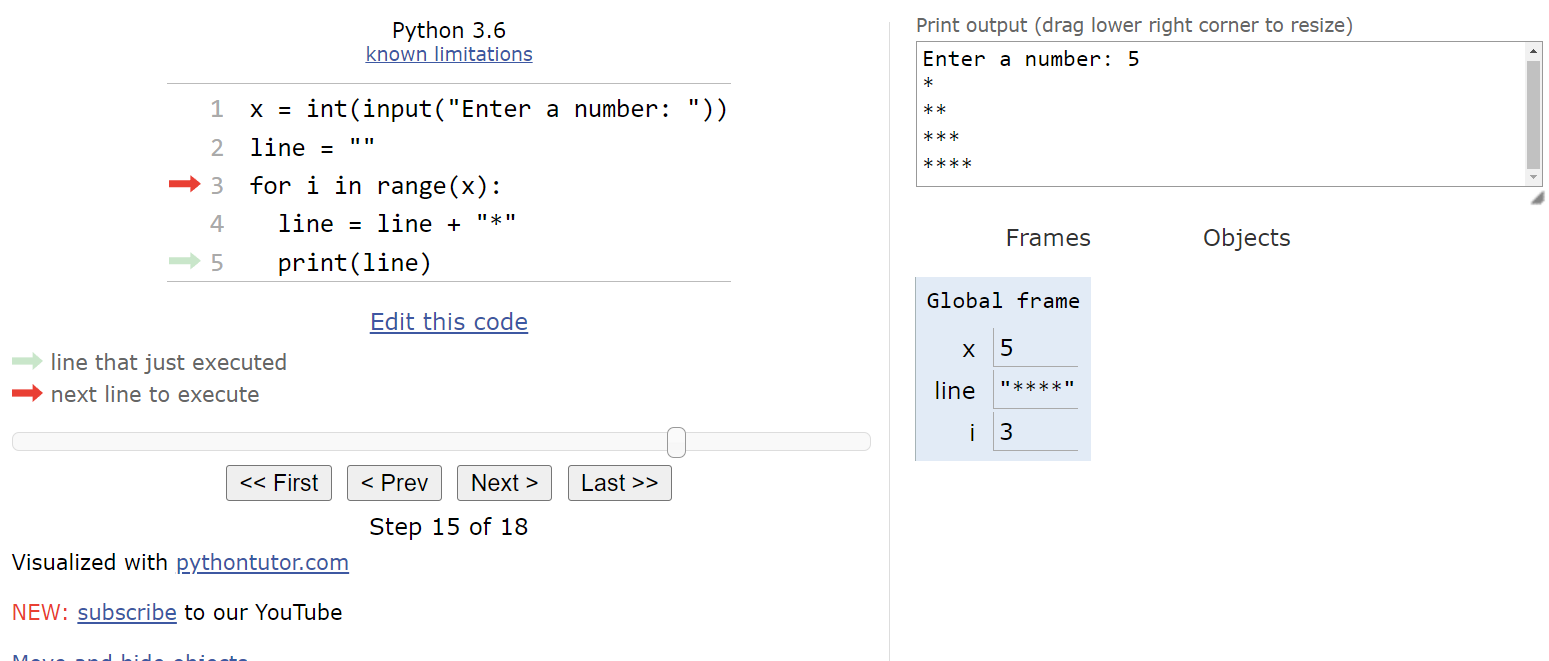
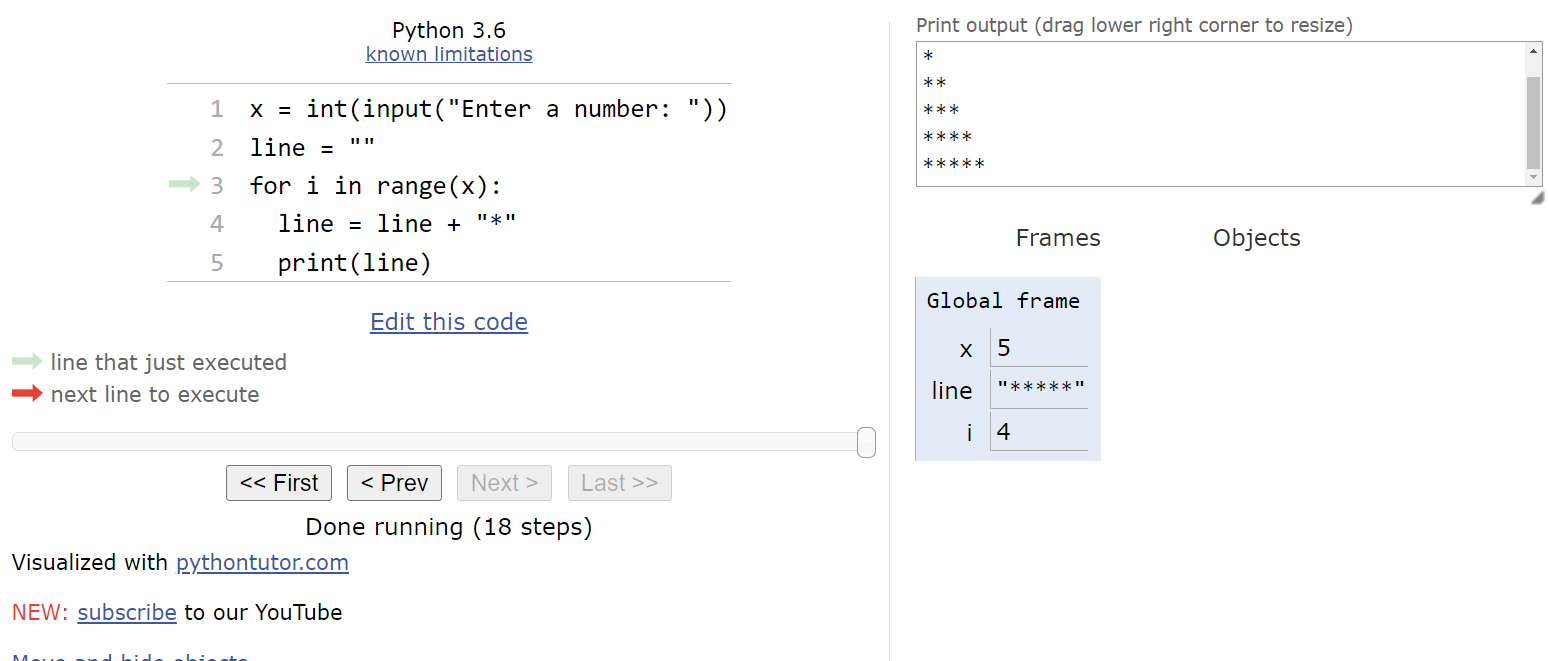
By now, we should have a pretty good idea of what this loop does. There’s one more item in the list, so we’ll update i to be
$ 4 $:
Inside the loop, we’ll add one more asterisk to line and then print it.
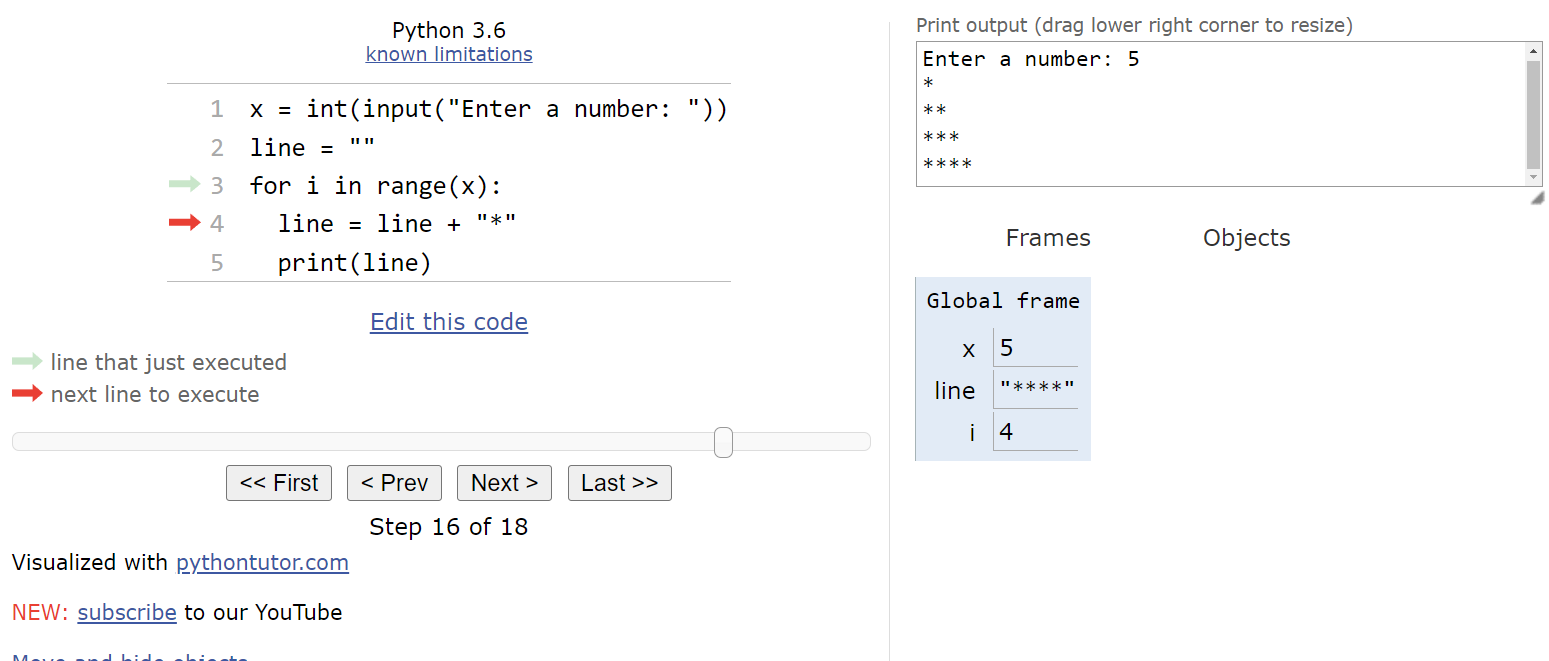
Finally, we’re back at the top of the loop. Since there are no more items left in the list, we can jump to the bottom of the for loop and continue the program from there.
In this case, there’s no more code left in the main() function, so it will end and the program will terminate.
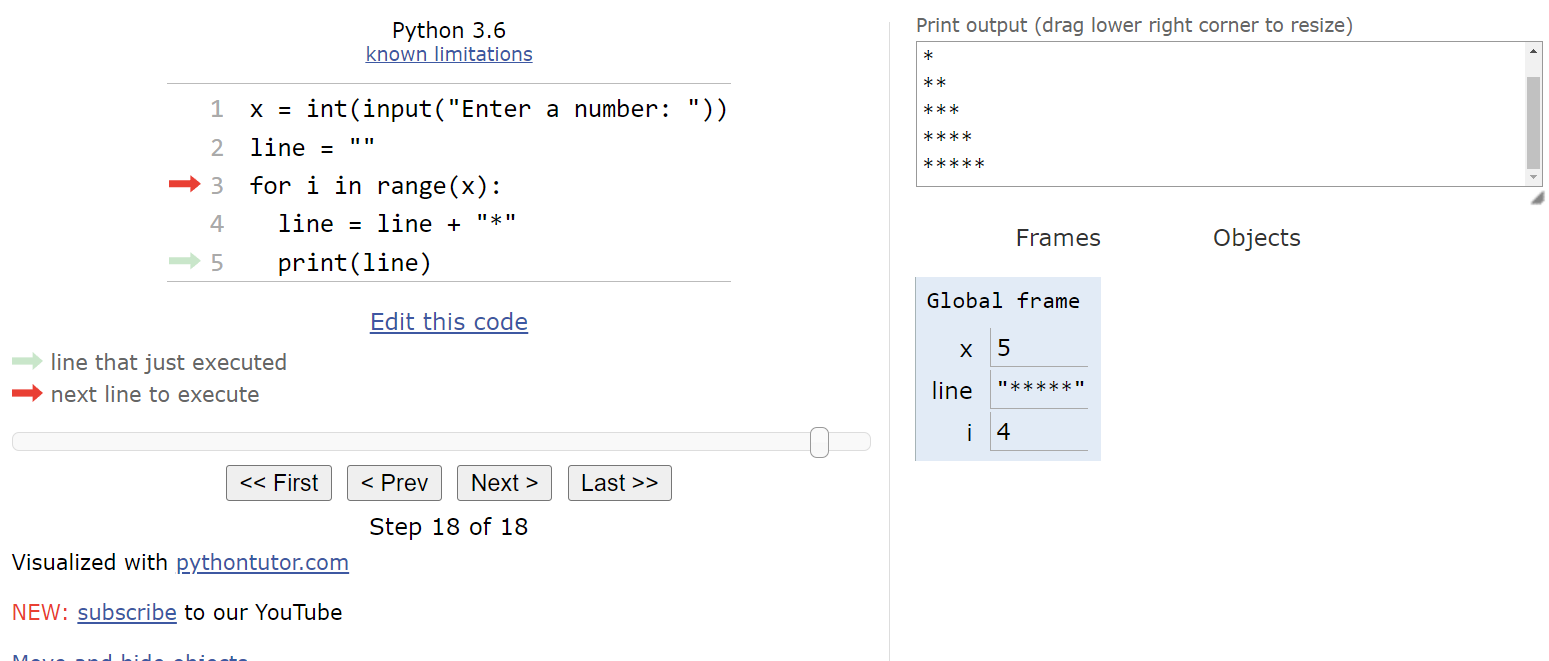
Looking at the output, we see that this program will print a right triangle of asterisks that is x lines tall and x characters wide at the bottom.
A full execution of this program is shown in this animation.
As we can see, working with for loops in Python is a quick and easy way to repeat a block of statements a specific number of times using the range() function.
Converting to a While Loop
It is possible to convert any for loop using the range() function in Python to a while loop. This can be done following a simple three-step pattern:
- Set an initial value for the iterator variable before the loop
- Update the iterator value at the end of each loop iteration
- Convert to a while loop and check the ending value of the iterator variable in the Boolean expression
Let’s look at the code from the example above:
x = int(input("Enter a number: "))
line = ""
for i in range(x):
line = line + "*"
print(line)To convert this for loop into a while loop, we can follow the three steps listed above. First, we must set an initial value for our iterator variable i before the loop. Since the first value stored in i is
$ 0 $, we’ll set it to that value.
x = int(input("Enter a number: "))
line = ""
i = 0
for i in range(x):
line = line + "*"
print(line)Next, we need to update the value of the iterator variable at the end of each loop iteration. Since we didn’t provide an argument for the step value in the range() function, we know that i will just be incremented by
$ 1 $ each time. So, we’ll add a short line to increment i at the bottom of the loop:
x = int(input("Enter a number: "))
line = ""
i = 0
for i in range(x):
line = line + "*"
print(line)
i = i + 1Finally, we can switch the for loop to a while loop. In the Boolean expression, we want to repeat the loop while the iterator variable i has not reached the maximum value. So, we’ll use the Boolean expression i < x in the new while loop:
x = int(input("Enter a number: "))
line = ""
i = 0
while i < x:
line = line + "*"
print(line)
i = i + 1There we go! That’s the basic process for converting any for loop using range() in Python to be a while loop. It’s a useful pattern to know and recognize when it is used in code.
Subsections of For Loops
Input with Loops
YouTube VideoResources
Loops in Python are also a great way to handle situations where a user must input a value that meets certain criteria. Previously, we used an if statement to determine if the input was valid, but if it wasn’t valid all we could do was print an error and end the program. If we use a loop instead, we can prompt the user to provide additional input until we receive a valid value.
To make this process easy to use, we can develop a block of code just to handle input from the user. For example, if we want the user to input a percentage, we could use code similar to this:
x = float(input("Enter a percentage as a decimal number from 0 to 1: "))
while(x < 0 or x > 1):
print("Invalid Input!")
x = float(input("Enter a percentage as a decimal number from 0 to 1: "))This code starts by prompting the user to input a number, and stores it as a floating-point value in the variable x. Then, it will reach the start of the while loop. The Boolean expression will check to see if the value provided is not a percentage, so if it is less than
$ 0 $ or greater than
$ 1 $ it is considered invalid.
If the input is invalid, we’ll print an error and prompt the user for input again. We’ll keep repeating this process until the user provides a value between
$ 0 $ and
$ 1 $, at which point the loop will terminate. At this point, we know that the value stored in x is a valid value.
Reading Input
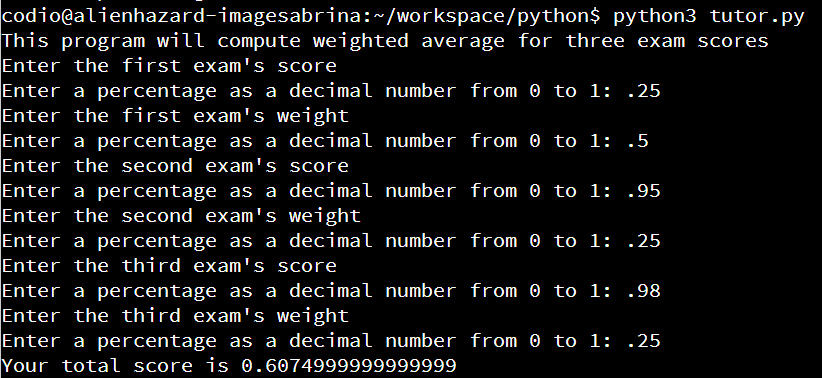
With code such as that in our program, we can use it to actually read input directly from the user. For example, we can write a quick program to calculate a weighted average of exam scores as shown below:
print("This program will compute weighted average for three exam scores")
print("Enter the first exam's score")
x = float(input("Enter a percentage as a decimal number from 0 to 1: "))
while(x < 0 or x > 1):
print("Invalid Input!")
x = float(input("Enter a percentage as a decimal number from 0 to 1: "))
exam1_score = x
print("Enter the first exam's weight")
x = float(input("Enter a percentage as a decimal number from 0 to 1: "))
while(x < 0 or x > 1):
print("Invalid Input!")
x = float(input("Enter a percentage as a decimal number from 0 to 1: "))
exam1_weight = x
print("Enter the second exam's score")
x = float(input("Enter a percentage as a decimal number from 0 to 1: "))
while(x < 0 or x > 1):
print("Invalid Input!")
x = float(input("Enter a percentage as a decimal number from 0 to 1: "))
exam2_score = x
print("Enter the second exam's weight")
x = float(input("Enter a percentage as a decimal number from 0 to 1: "))
while(x < 0 or x > 1):
print("Invalid Input!")
x = float(input("Enter a percentage as a decimal number from 0 to 1: "))
exam2_weight = x
print("Enter the third exam's score")
x = float(input("Enter a percentage as a decimal number from 0 to 1: "))
while(x < 0 or x > 1):
print("Invalid Input!")
x = float(input("Enter a percentage as a decimal number from 0 to 1: "))
exam3_score = x
print("Enter the third exam's weight")
x = float(input("Enter a percentage as a decimal number from 0 to 1: "))
while(x < 0 or x > 1):
print("Invalid Input!")
x = float(input("Enter a percentage as a decimal number from 0 to 1: "))
exam3_weight = x
total = exam1_score * exam1_weight + exam2_score * exam2_weight + exam3_score * exam3_weight
print(f"Your total score is {total}")A quick execution of this program is shown here:
Take a minute to confirm that the program works by running it yourself, either in Python Tutor or directly in Python. You can even adapt this program to help calculate your final grade in this course!
Learning to how to create building blocks of larger programs, such as loop for checking input described here, is a great way to develop our programming skills. If we can learn to take a large program and break it down into smaller, repeatable chunks, then the entire program becomes much easier to develop and maintain.
Are you starting to ask yourself if there is a better way to handle repeated blocks of code like this? If so, that’s great! We’ll cover functions, which is a way to build repeatable pieces of code that can be used throughout our programs, in the next chapter!
Subsections of Input with Loops
Testing Loops
YouTube VideoResources
Another important aspect of working with loops in code is learning how to properly test programs that contain loops. So, let’s look at some of the methods we can use when testing our programs containing loops to make sure they work correctly and won’t run into any problems.
Branch and Path Coverage
Loops, like conditional statements, introduce different branches and paths into our programs. So, one of the first steps when testing these programs is to develop a set of inputs that will execute each branch of the code, as well as finding inputs that will execute multiple different paths through the program. Since loops may repeat many times, typically we only worry about two possible paths when dealing with loops - one path where it is skipped entirely and another path where the loop is entered at least once.
Let’s consider this simple Python program that contains loops:
x = int(input("Enter a number: "))
y = int(input("Enter a number: "))
i = 0
line = ""
while i < x + y:
line = line + "*"
print(line)
i = i + 1
while i > x - y:
print("=", end="")
i = i - 1
print()This program will simply print a right triangle of asterisks * that is x + y characters wide and tall, similar to a previous example in this lab. However, it will also print a final line of equals signs = below that, consisting of x - y characters. To test this program, we want to try and find some input values for x and y that achieve branch and path coverage.
Branch Coverage
To achieve branch coverage, we want to execute each line of code in this program at least once. An easy way to do that is to provide inputs so that the sum of x and y is a positive number in order to enter the first loop. After the first loop terminates, the value of i will be equal to the sum of x and y, provided that value is greater than
$ 0 $. So, in order to also enter the second loop, we need to make sure the difference of x and y is smaller than their sum.
A set of inputs that achieves this would be
$ 3 $ and
$ 1 $ for x and y, respectively. Their sum is
$ 4 $, so the first loop will be executed 4 times. Then, the difference between the values is
$ 2 $, so the second loop will executed twice to reduce the value in i to
$ 2 $.
So, we can say that the inputs 3 and 1 are enough to achieve branch coverage.
Path Coverage
To achieve path coverage, we must consider three additional paths through the program:
- Neither loop is entered
- Only the first loop is entered
- Only the second loop is entered
First, in order to enter neither loop, we must have a set of inputs where the sum is less than or equal to $ 0 $, and also where the difference is less than or equal to $ 0 $. The simplest way to achieve this is to set both inputs to exactly $ 0 $! Sometimes the simplest inputs are the easiest for testing.
To enter the first loop only, we need the situation where the sum of x and y is greater than 0, but then their difference is even larger. An easy way to accomplish this is to set y to a small negative number. For example, we could set x to
$ 3 $ and y to
$ -1 $. That will make their sum
$ 2 $ but the difference
$ 4 $, so we’ll only execute the first loop but not the second one.
Finally, if we want to execute the second loop only, we need to make both the sum and the difference of x and y a number less than
$ 0 $. In that case, we can simply set both x and y to negative values, but make sure that x is overall a smaller value than y. So, we could set x to
$ -3 $ and y to
$ -1 $. In that case, their sum is
$ -4 $ but their difference is
$ -2 $. That will cause the program to skip the first loop but enter the second loop.
So, we can achieve path coverage with these four sets of inputs:
3, 10, 03, -1-3, -1
Loop Termination
When testing loops, we should also check to make sure that the loops will eventually terminate if we ever enter them. Thankfully, in this program, it is very easy to reason about this and convince ourselves that it works.
Consider the first loop - the only way to enter that loop is if the value of i is less than the sum of x and y, and each time the loop iterates the value in i will be incremented by
$ 1 $. Since i is getting larger each time, eventually it will reach a value that is greater than or equal to x + y and the loop will terminate.
The same argument can be made for the second loop. In that loop, i is initially greater than the difference of x and y, but i is decremented each time, so eventually the loop will terminate.
Technically speaking, we can come up with a loop variant for each loop and show that it is monotonically decreasing. This is easily done by simply finding the difference between the iterator variable i and the termination condition of the loop, either the sum or the difference of x and y. We won’t ask you to get to this level of detail when testing your own loops, but it is a very useful concept to understand when working with loops.
There we go! We were able to quickly come up with a set of inputs that will execute all possible branches and paths in this program, and we can also show that each of the loops will properly terminate anytime they are executed. So, we know that our program at least won’t crash, no matter what integers are provided as input. We can also examine the output of each test and make sure that it matches what the expected output should be in order to show that our program not only doesn’t crash, but that it provides the correct output.
Subsections of Testing Loops
Worked Example
YouTube VideoResources
Now that we’ve learned all about using loops in Python, let’s go through a complete worked example to see how all the pieces fit together. As we continue to develop larger and more complex programs, it is helpful to observe the entire process from start to finish so we can see how to easily develop a program one step at a time. Once we’ve created our program, we’ll also perform a bit of testing to make sure that it works correctly.
Problem Statement
For this example, let’s write a program to play a simple number guessing game. Here’s how it works:
The game will select two random numbers from $ 0 $ to $ 100 $, one for each player. Then, each player will guess a number in the range, and the game will print either “higher” if that player’s secret number is larger than the guess, or “lower” if the player’s secret number is smaller than the guess. Players will alternate turns until one player correctly guesses their secret number and wins the game.
This game is pretty simple, but there are still quite a few different parts that we need to build in order to write the entire program. So, let’s go through the process of building a complete program in Python to play this game.
Random Numbers
Before we start building our program, we need some way to generate a random number. Thankfully, Python has a built-in library called random that has many functions for working with random numbers in our programs.
To use a library in Python, we must first import it into our code. This is done using a simple import statement at the very top of our program’s code, followed by the name of the library we want to use. So, for this library, we’ll need to have the following import statement at the top of our source code:
import randomOnce we’ve done that, we can use the function random.randint(a, b) to generate a random number that is between a and b, inclusive. Mathematically, we can say that it generates an integer
$ x $ such that
$ a <= x <= b $.
So, here’s a quick test program we can use to explore how to use random numbers in Python:
import random
a = int(input("Enter a minimum value: "))
b = int(input("Enter a maximum value: "))
x = random.randint(a, b)
print(f"A random number between {a} and {b} is {x}")Take a minute to run this program and modify it a bit to make sure you understand how to work with random numbers in Python before continuing.
Basic Structure
For this program, we need to start by generating two random numbers from
$ 0 $ to
$ 100 $, one for each player. So, we can create and store those numbers in the code, and we’ll also need to import the random library at the top of our file.
import random
p1_secret = random.randint(0, 100)
p2_secret = random.randint(0, 100)Once we have the secret numbers, then we can sketch out the game itself. We’ll use a while loop to repeat until a player has guessed correctly, and we’ll also use a simple integer variable to keep track of the current player. Inside of the loop, we should get a new guess from a player, and also switch between players. So, let’s add that to our program structure using some comments:
import random
p1_secret = random.randint(0, 100)
p2_secret = random.randint(0, 100)
player = 1
while( ): # player has not guessed correctly
# swap player
# get new guess from player
# check if secret is higher or lowerFrom here, we can start to work on the actual logic in our program.
Boolean Expression
The trickiest part of this program is coming up with the correct Boolean expression to use in our while loop. That helps us determine if the player has guessed correctly and that the loop should stop. However, this is a bit complex since there are two different players, each one with their own secret number. So, in our Boolean expressions, we have to determine what the current player is as well as whether the most recent guess was correct.
To do this, we can use the and and or Boolean operators to combine several Boolean expressions together. For example, we can determine if the current player is player 1 using player == 1, and then we can determine if the most recent guess is equal to player 1’s secret number using guess == p1_secret. If we want both of those to be True in order to exit the loop, we can combine them using the and operator. We can do something very similar for player 2 as well. Then, if we want the loop to terminate if either of those is true, we can combine the two statements using the or operator.
So, all together, we want to repeat the loop as long as that entire statement is not True. So, the full Boolean expression would be:
not ((player == 1 and guess == p1_secret) or (player == 2 and guess == p2_secret))That’s pretty complex, but it easily encompasses all of the rules of the game!
Handling Input
To get input from the user, we can write a simple loop to handle input is very similar to the ones we saw earlier in this lab. We simply want to make sure the user has provided a value that is between $ 0 $ and $ 100 $, and prompt the user for another input if not. We’ll also add in a variable to print the current player in the prompt for input.
So, our loop to get input might look something like this:
x = int(input(f"Enter a guess for player {player}: "))
while x < 0 or x > 100:
print("Invalid Input!")
x = int(input(f"Enter a guess for player {player}: "))Then, in our code, we can simply use the new input loop to read a player’s current guess as shown here:
import random
p1_secret = random.randint(0, 100)
p2_secret = random.randint(0, 100)
player = 1
while(not ((player == 1 and guess == p1_secret) or (player == 2 and guess == p2_secret))): # player has not guessed correctly
# swap player
x = int(input(f"Enter a guess for player {player}: "))
while x < 0 or x > 100:
print("Invalid Input!")
x = int(input(f"Enter a guess for player {player}: "))
guess = x
# check if secret is higher or lowerChecking Guess and Swapping Players
Next, we need to add some conditional statements to check if the secret is higher or lower than the guess, and also to swap between players. First, let’s look at swapping players. This is pretty simple, since all we need to do is find out what the current player is, and switch that value to the other player. So, we can do that using a simple if statement as shown here:
import random
p1_secret = random.randint(0, 100)
p2_secret = random.randint(0, 100)
player = 1
while(not ((player == 1 and guess == p1_secret) or (player == 2 and guess == p2_secret))): # player has not guessed correctly
if player == 1:
player = 2
else:
player = 1
x = int(input(f"Enter a guess for player {player}: "))
while x < 0 or x > 100:
print("Invalid Input!")
x = int(input(f"Enter a guess for player {player}: "))
guess = x
# check if secret is higher or lowerThe process for checking a guess is very similar - we can simply check to see if the guess is higher or lower than the secret for the current player, and print the output accordingly. First, we’ll need to figure out the current player:
if player == 1:
# check player 1's secret
else:
# check player 2's secretThen, in each of those branches, we’ll check the guess:
if player == 1:
if guess < p1_secret:
print("Higher")
elif guess > p1_secret:
print("Lower")
else:
print("Correct!")
else:
if guess < p2_secret:
print("Higher")
elif guess > p2_secret:
print("Lower")
else:
print("Correct!")This is a pretty straightforward set of conditional statements, but it goes to show how many lines of code are required even for a simple guessing-game program like this one.
Initial Testing and Debugging
So, at this point, we can put all of the pieces together and test our program. Here is the complete program that we’ve written so far:
import random
p1_secret = random.randint(0, 100)
p2_secret = random.randint(0, 100)
player = 1
while(not ((player == 1 and guess == p1_secret) or (player == 2 and guess == p2_secret))): # player has not guessed correctly
if player == 1:
player = 2
else:
player = 1
x = int(input(f"Enter a guess for player {player}: "))
while x < 0 or x > 100:
print("Invalid Input!")
x = int(input(f"Enter a guess for player {player}: "))
guess = x
if player == 1:
if guess < p1_secret:
print("Higher")
elif guess > p1_secret:
print("Lower")
else:
print("Correct!")
else:
if guess < p2_secret:
print("Higher")
elif guess > p2_secret:
print("Lower")
else:
print("Correct!")So, let’s try to run this program and see if it works. Unfortunately, right from the start we have an error in our code, since when we try to execute this program, we’ll get the following error:
Take a minute to see if you can spot and fix the error before continuing!
Unfortunately, in our Boolean expression inside of the while loop, we’re referencing the guess variable, but that variable isn’t actually created until later inside the while loop itself. So, we’ll need to set the guess variable to a value outside of the while loop first.
Also, we must be very careful about what value we use. If we set guess to be
$ 0 $ initially, there is a very small chance that player 1 could win the game immediately if their secret number is
$ 0 $, since that is a valid guess. Instead, let’s set guess to be
$ -1 $ so that it will never be equal to a secret number.
After we make that change, when we run the program again, we may notice one other error:
Can you spot it by looking at this screenshot?
Unfortunately, our program starts with player 2’s turn instead of player 1. Why is that? Well, if we look closely at our code, we see that we are initially setting the player to player 1, but then immediately switching players inside of the while loop before we prompt for input. If we think about it, we can’t move the code that swaps players to later in the while loop, because then our Boolean expression to determine if the while loop should terminate will be incorrect. So, instead, we can simply initialize the player variable to be
$ 2 $, and then it will be switched to
$ 1 $ before we prompt for input the first time.
So, our final working program’s code with these two changes is shown here:
import random
p1_secret = random.randint(0, 100)
p2_secret = random.randint(0, 100)
player = 2
guess = -1
while(not ((player == 1 and guess == p1_secret) or (player == 2 and guess == p2_secret))): # player has not guessed correctly
if player == 1:
player = 2
else:
player = 1
x = int(input(f"Enter a guess for player {player}: "))
while x < 0 or x > 100:
print("Invalid Input!")
x = int(input(f"Enter a guess for player {player}: "))
guess = x
if player == 1:
if guess < p1_secret:
print("Higher")
elif guess > p1_secret:
print("Lower")
else:
print("Correct!")
else:
if guess < p2_secret:
print("Higher")
elif guess > p2_secret:
print("Lower")
else:
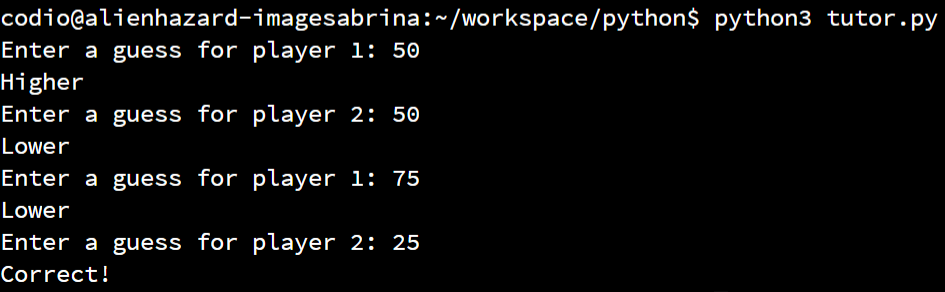
print("Correct!")A full example of running this program, complete with a very lucky guess, is shown in the screenshot below:
Testing - Branch and Path Coverage
Now that we have a complete and working program, let’s look at what it might take to test it. Unfortunately, testing a program that uses random numbers can be very tricky, since each time you run the program you might receive different outputs even if you provide the same inputs.
Thankfully, we can still perform some testing to achieve branch and path coverage by choosing our guesses carefully. Here are the basic methods we’ll want to try:
- Guessing
$ 0 $ for each player should result in
"Higher"for output, unless the secret number is $ 0 $. - Guessing
$ 100 $ for each player should result in
"Lower"for output, unless the secret number is $ 100 $. - Guessing the same value for one player while actually playing the game for the other player will eventually result in an output of
"Correct". Using a bit of logic, it is always possible to win the game in no more than $ 7 $ guesses. - Trying to input an invalid value should result in
"Invalid Input!"for output at least once.
Following those simple strategies and keeping track of the various outputs received, it is pretty easy to eventually test all branches and most, if not all, possible paths through the program.
Testing - Loop Termination
Checking for loop termination on this program is a bit trickier, since the secret numbers are random and the guesses that a player makes are also unpredictable. So, while we can’t say for sure that the program will terminate, we can always prove that there is a possible condition where the loop will terminate, and that condition depends entirely on the user providing the correct input. So, as long as it is possible, we can say that the loop is at least not an infinite loop, and the program will work correctly if the user makes the correct guess.
There we go! We’ve just explored a complete example of writing a program in Python, complete with loops and conditional statements. We also introduced random numbers and how we can easily use those in our programs. Beyond that, we explored how to test these programs and correct minor errors found in testing. Hopefully this process is very helpful as we continue to work on larger and more complex programs.
Subsections of Worked Example
Loops Practice
Let’s try some simple practice problems. These problems are not graded - they are just for you to practice before doing the real exercises in the lab itself. You can find the answers below each question by clicking the button below each question.
5.1 Reading Code
Consider the following pseudocode program:
x = int(input("Enter a positive integer: "))
while(x <= 0):
print("Invalid Input!")
x = int(input("Enter a positive integer: "))
a = 1
for i in range(9):
if x % a == 0:
print(f"{a}")
a = a + 1Explain, in your own words, the output that this program produces in relation to the input provided.
A fully correct answer is a succinct description of the output as it relates to the input. A partially correct answer is a step-by-step description of each line in the program and the output it will produce based on the input.
5.2 Testing Code
Consider the program above. Devise a set of inputs that will cause each of the 9 possible numerical outputs to print at least once, and for each input, list the numbers that will be printed as output.
5.3 Reading Code
Consider the following Python program:
x = int(input("Enter a positive integer: "))
while(x <= 0):
print("Invalid Input!")
x = int(input("Enter a positive integer: "))
a = ""
while x > 0:
if x % 2 == 0:
a = "0" + a
else:
a = "1" + a
x = x // 2
print(a)Explain, in your own words, the output that this program produces in relation to the input provided.
A fully correct answer is a succinct description of the output as it relates to the input. A partially correct answer is a step-by-step description of each line in the program and the output it will produce based on the input.
Hint: when numbers are stored digitally on a computer, what numerical format is used?
5.4 Testing Code
Consider the Python program above. Devise a set of inputs that you feel are sufficient to test the program, and briefly explain why those inputs are sufficient.
Hint: Achieving coverage is very simple, but providing enough input to be confident that the program is generating the correct output should also be considered.
5.5 Writing Code
Write a complete Python program that meets the specification below.
The Fibonacci Sequence is a sequence of numbers where the next number is the sum of the previous two numbers. The sequence starts with the numbers $ 1 $ and $ 1 $, making the next number $ 2 $. The following number is $ 3 $, since it is the sum of the second and third number of the sequence. The sequence continues indefinitely.
For this program, ask the user to input a number that must be greater than $ 5 $. If the user inputs a number that is $ 5 $ or less, display an error and prompt the user for another input until a valid input is received.
Then, determine if the number provided as input is part of the Fibonacci Sequence. This can be done by computing the sequence one number at a time until the desired number is reached or passed. Print either "In sequence" or "Not in sequence" depending on the result found.
5.6 Writing Code
Write a complete Python program that meets the specification below.
Write a program that will print the first $ 30 $ multiples of a given number, but only multiples where the last digit is equal to a second given number.
For this program, ask the user to provide two integers - the first between $ 1 $ and $ 100 $, inclusive, and the second between $ 0 $ and $ 9 $, inclusive. If the user provides an invalid value for either input, print an error message and prompt the user for another input until a valid input is received.
Then, the program should compute the first $ 30 $ multiples of the first given number. This would be equivalent to multiplying the number by $ 1 $ all the way through multiplying the number by $ 30 $. Then, if that computed multiple ends with the same digit as the second number, it should be printed. Otherwise, no output is produced for that number.
For example, if the first given number is $ 9 $ and the second number is $ 1 $, then the output should be:
81
171
261Your program should make use of a for loop and the Python range() function.
Hint: what is the value of 81 % 10? What about 27 % 10? Does that value help you determine whether the number should be printed or not?
Nested While Loops
YouTube VideoResources
Up to this point, we explored how we can use iterative structures in our code, such as while loops and for loops, to repeat steps a certain number of times or while a Boolean condition is true. This is a very powerful tool, since it allows us to build programs that can repeatedly ask the user to provide input until a valid value is received, or even perform a repeated calculation until it reaches a desired result.
Loops, just like conditional statements, can also be nested inside of one another, allowing us to build even more complex programs. In fact, you may have already done this using loops and code that contains loops in a previous lab without realizing it. Next, we’ll explore how to combine loops in many different ways, and learn how we can test and debug these complex programs.
Later in this course, we’ll learn about two different collection types in Python, and we’ll quickly see how we can use loops to work with them quickly and easily.
Nested While Loops
To create a nested loop in Python, we can simply place a loop structure inside of the block of statements that is repeated by another loop structure. This is very similar to how we can nest conditional statements as well.
For example, consider this short Python program:
i = 1
while i < 10:
j = i
while j < 10:
print(f"{j} ", end="")
j = j + 1
print("")
i = i + 1
print("Complete!")In this example, we see a Python while loop that uses the variable i in its Boolean expression first, and then inside of that loop we see another loop that uses j in its Boolean expression. When we run this code, each time we execute the steps inside of the outer while loop, we’ll have to completely go through the inner while loop as well. It can be very complex to keep track of everything, but with a bit of practice we’ll learn some strategies for mentally working through loops.
Before continuing, take a look at that program’s code and see if you can determine what it will print!
Code Tracing Example
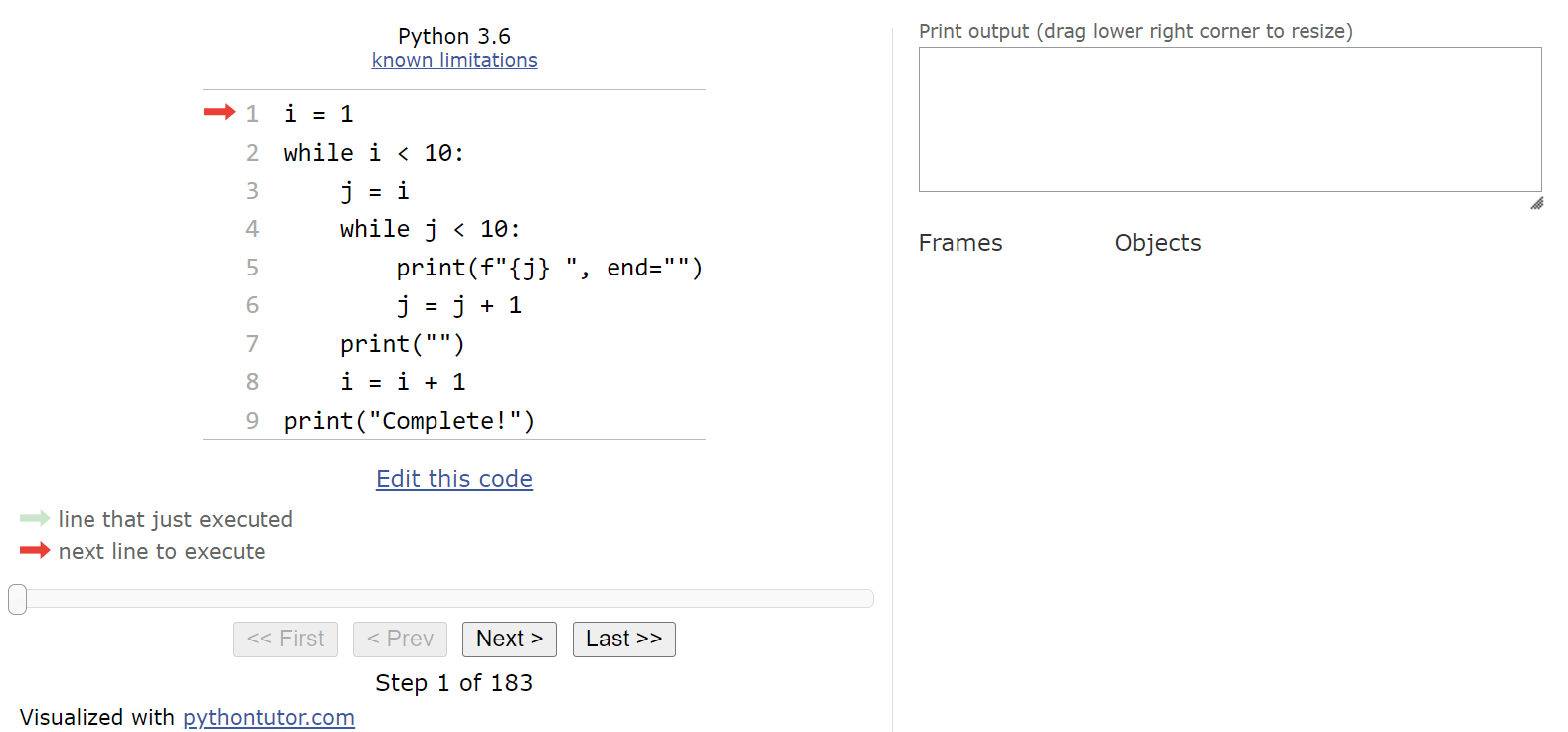
To really understand how a set of nested loops work, let’s go through a code tracing example using Python Tutor. To follow along, copy this code to Python Tutor or click this Python Tutor link to load Python Tutor in a web browser.
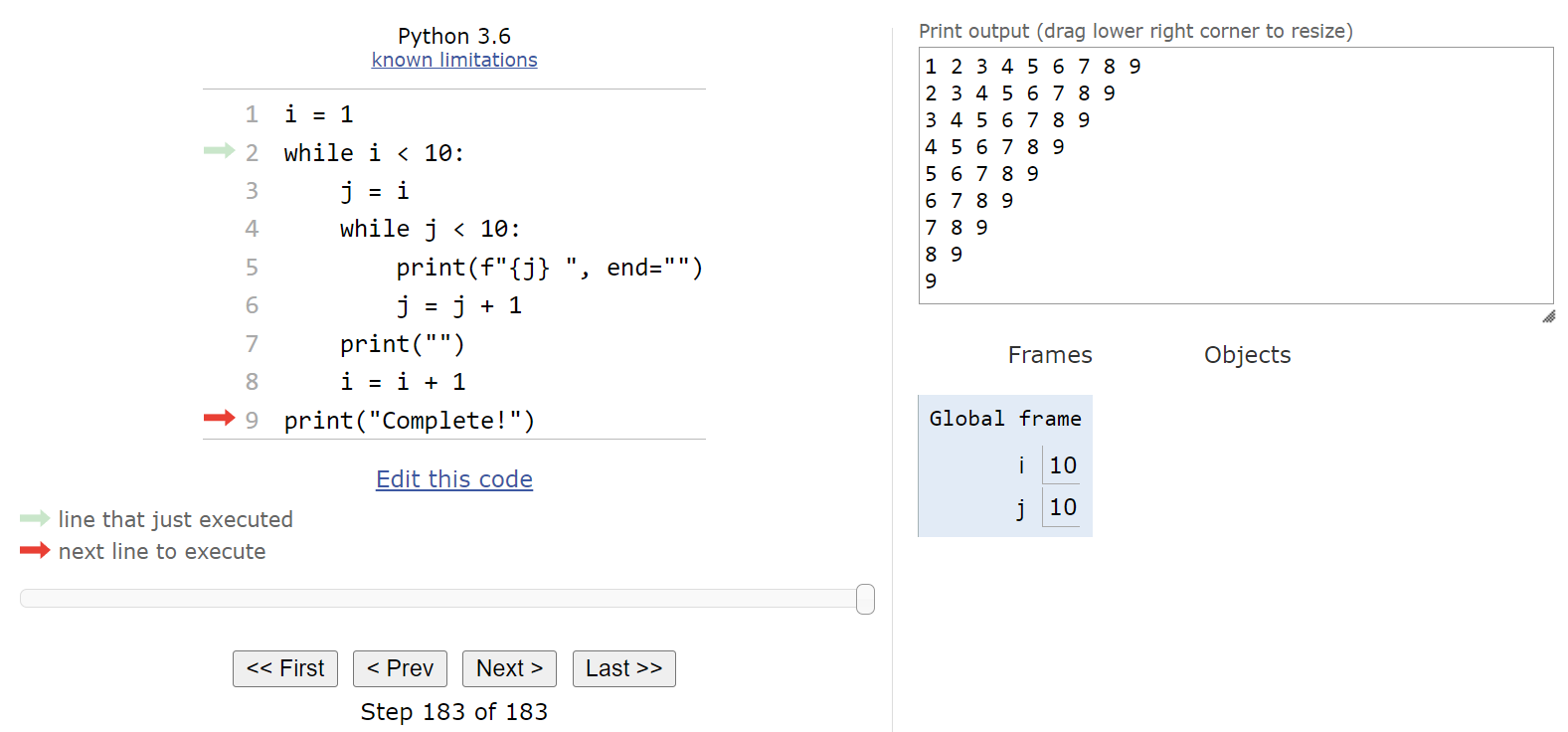
When we first load this code in Python Tutor, we should see the following state:
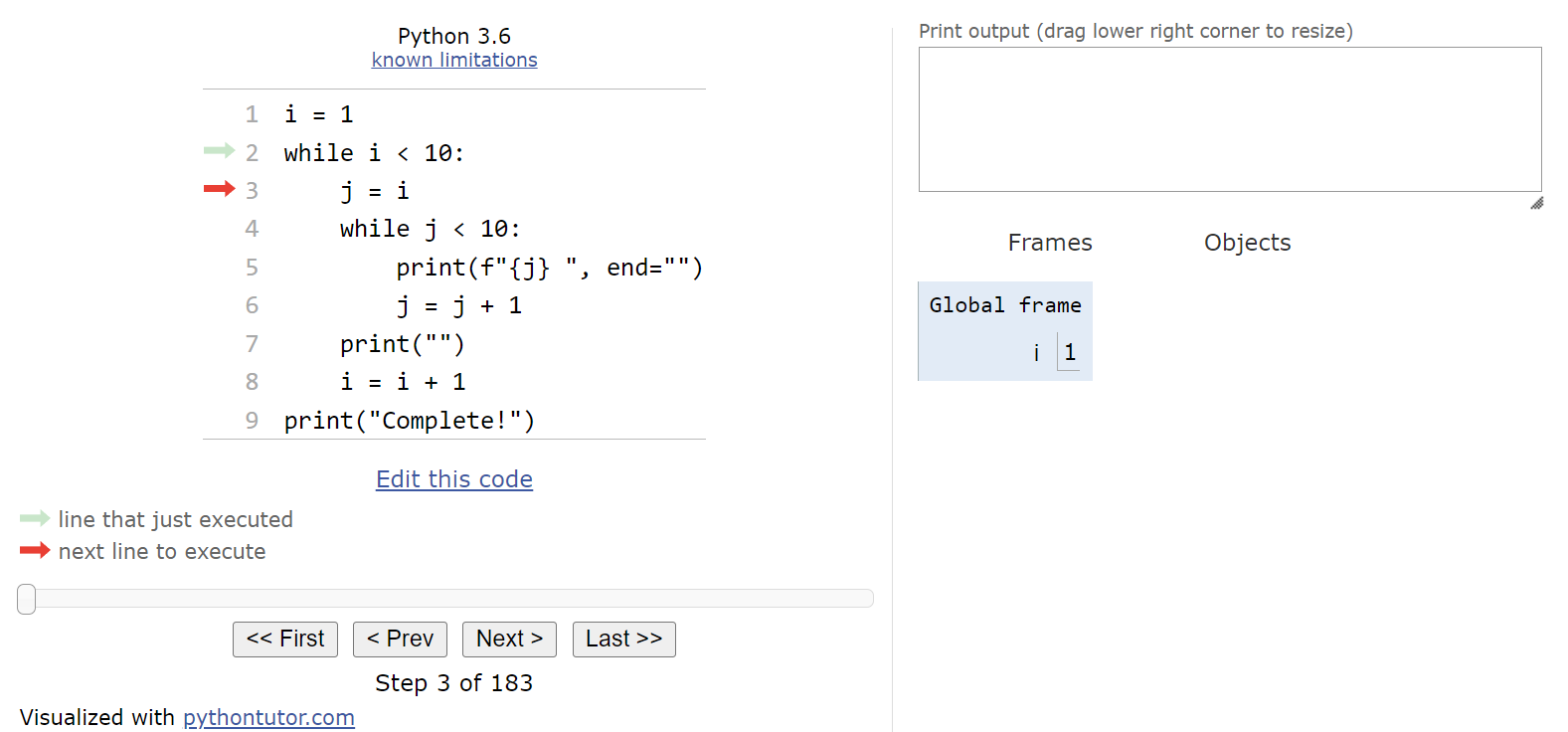
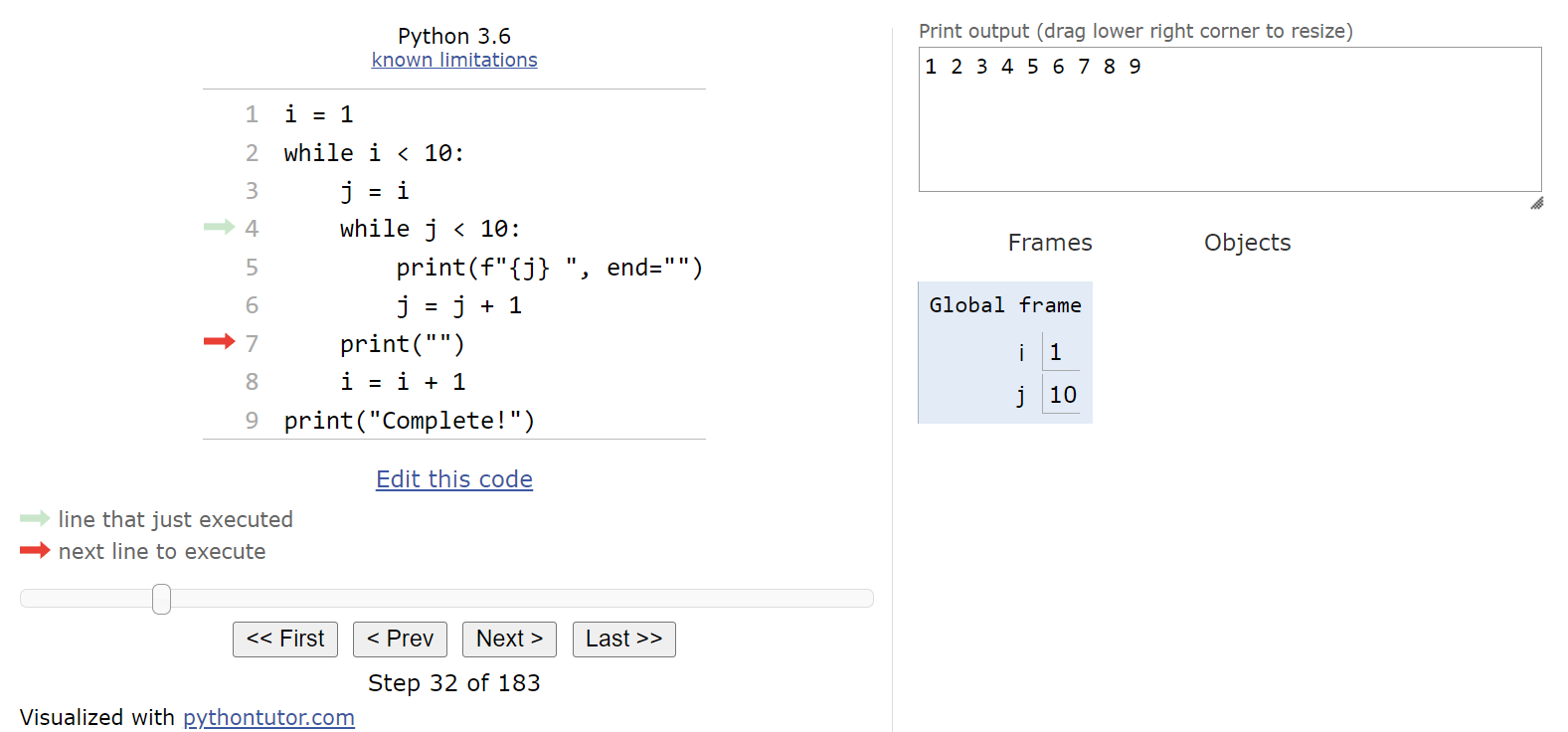
When we look at the bottom of the Python Tutor page, we’ll see that we are on step 1 of 183 steps! That’s a very large number of steps to deal with! Up to this point, most of our programs have been around 20 or 30 steps in total. So, already we’re seeing that nested loops can quickly create programs that execute many more steps.
Here, we are setting up the iterator variable i that is used for the outermost loop. So, we’ll store the value $1$ in i and then move to the next line:
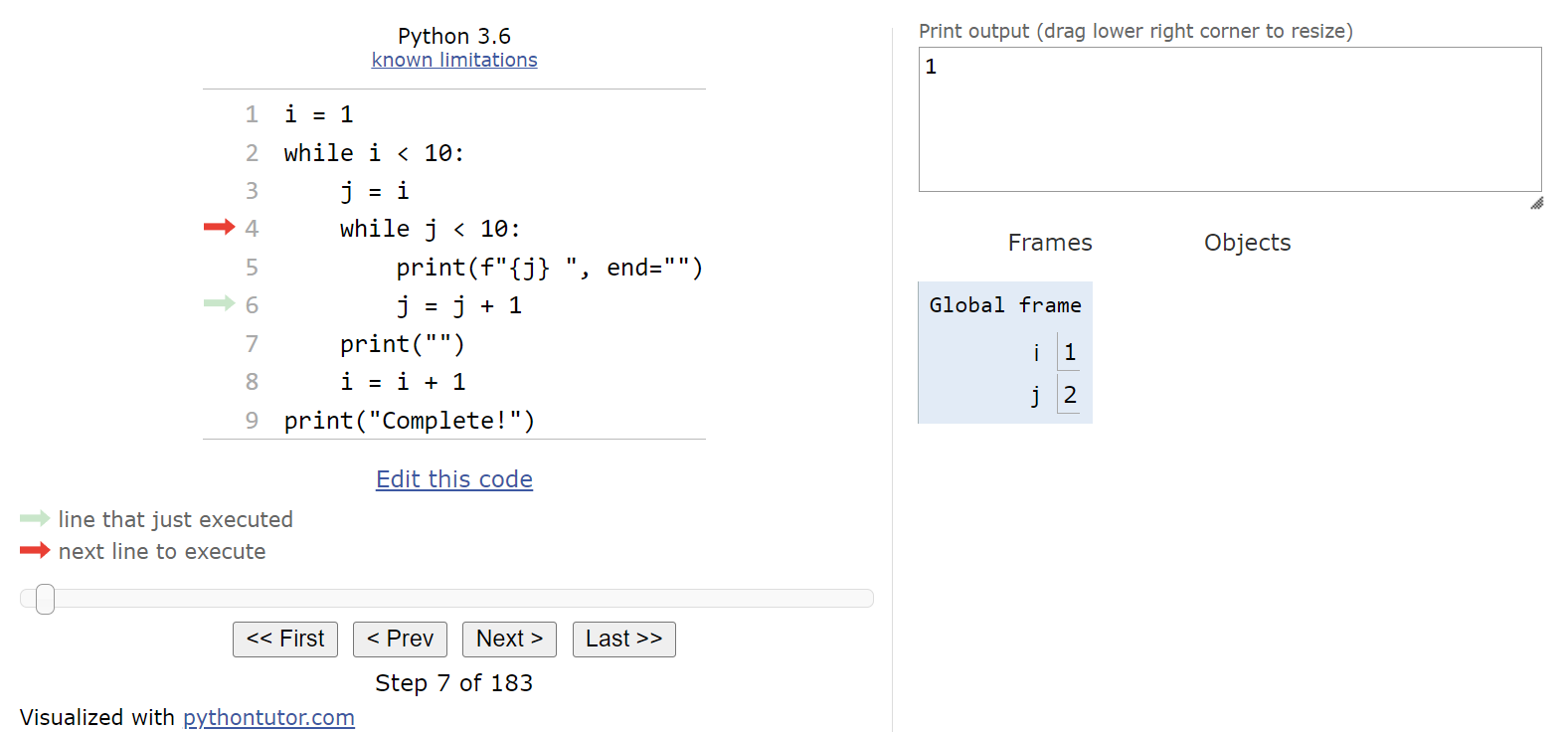
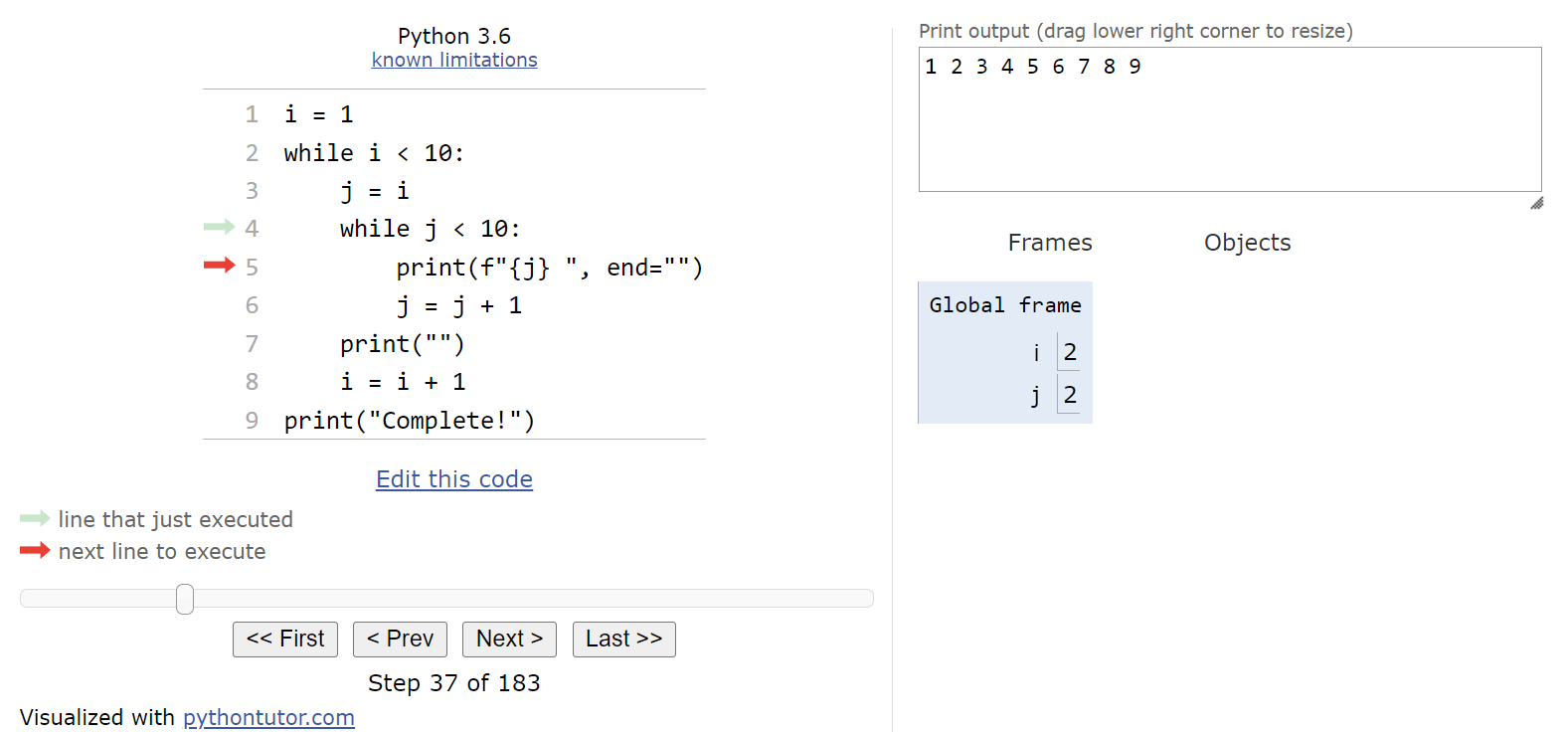
Now we’re at the start of our outer while loop. That means that we’ll need to evaluate the Boolean expression and determine if it is True or False. In this case, we can see that i < 10 will evaluate to True, so we should enter the loop.
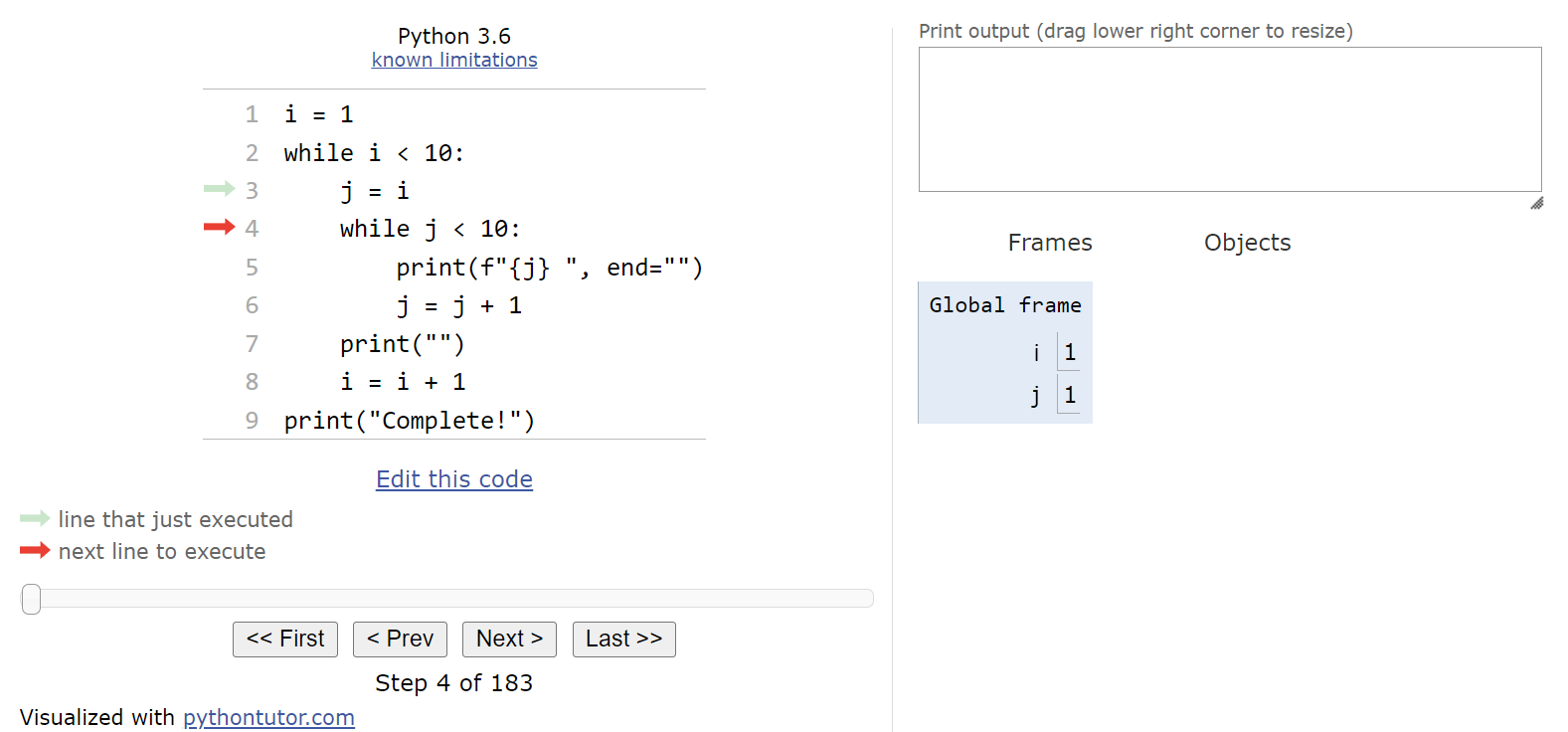
Once we are inside the loop, we’ll start setting up the iterator variable j for the inner loop. In this code, we are storing the current value of i in j, so at this point j will also contain $1$.
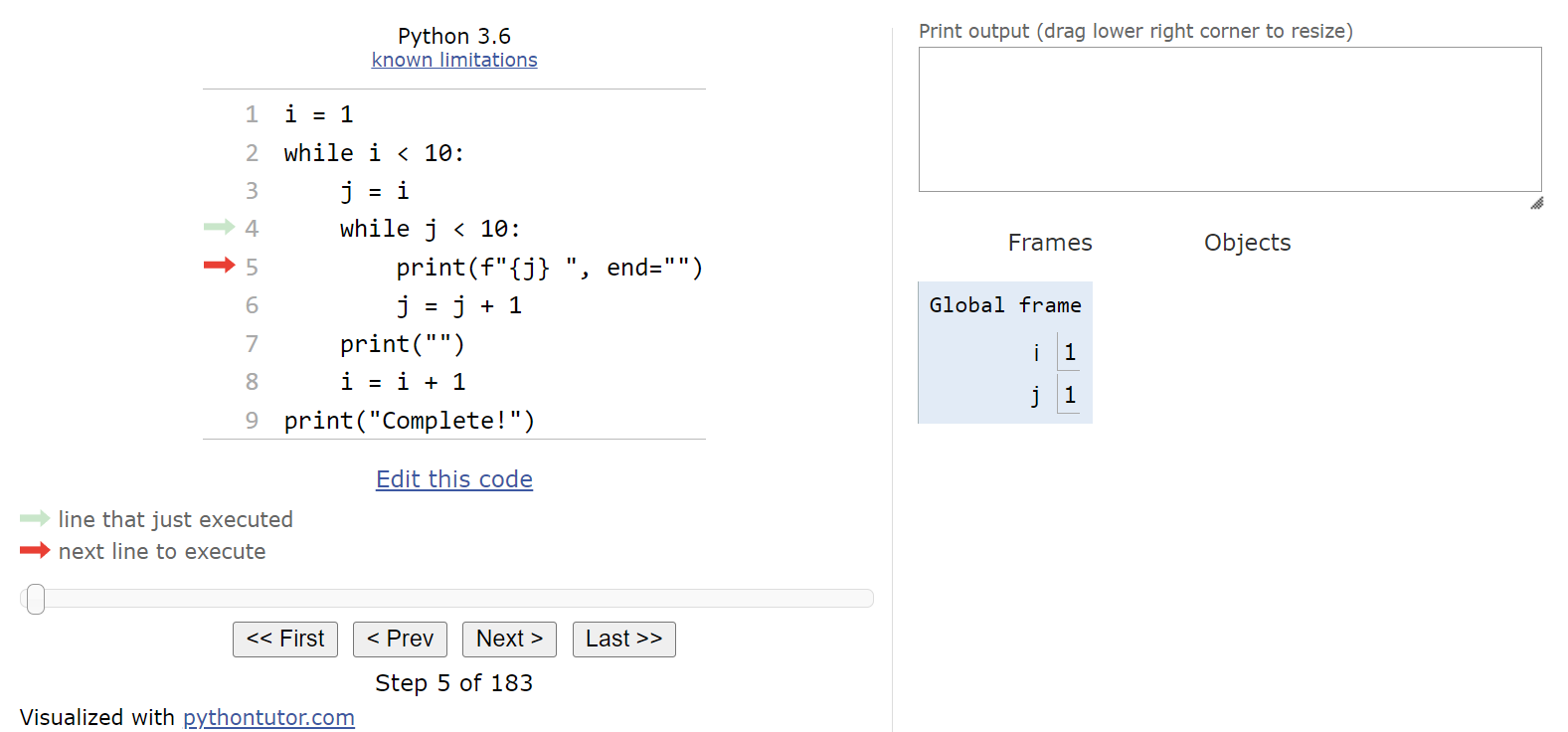
At this point, we need to decide if we should enter the inner while loop. So, once again we’ll look at the Boolean expression, j < 10, and see that it is also True and we should enter the loop.
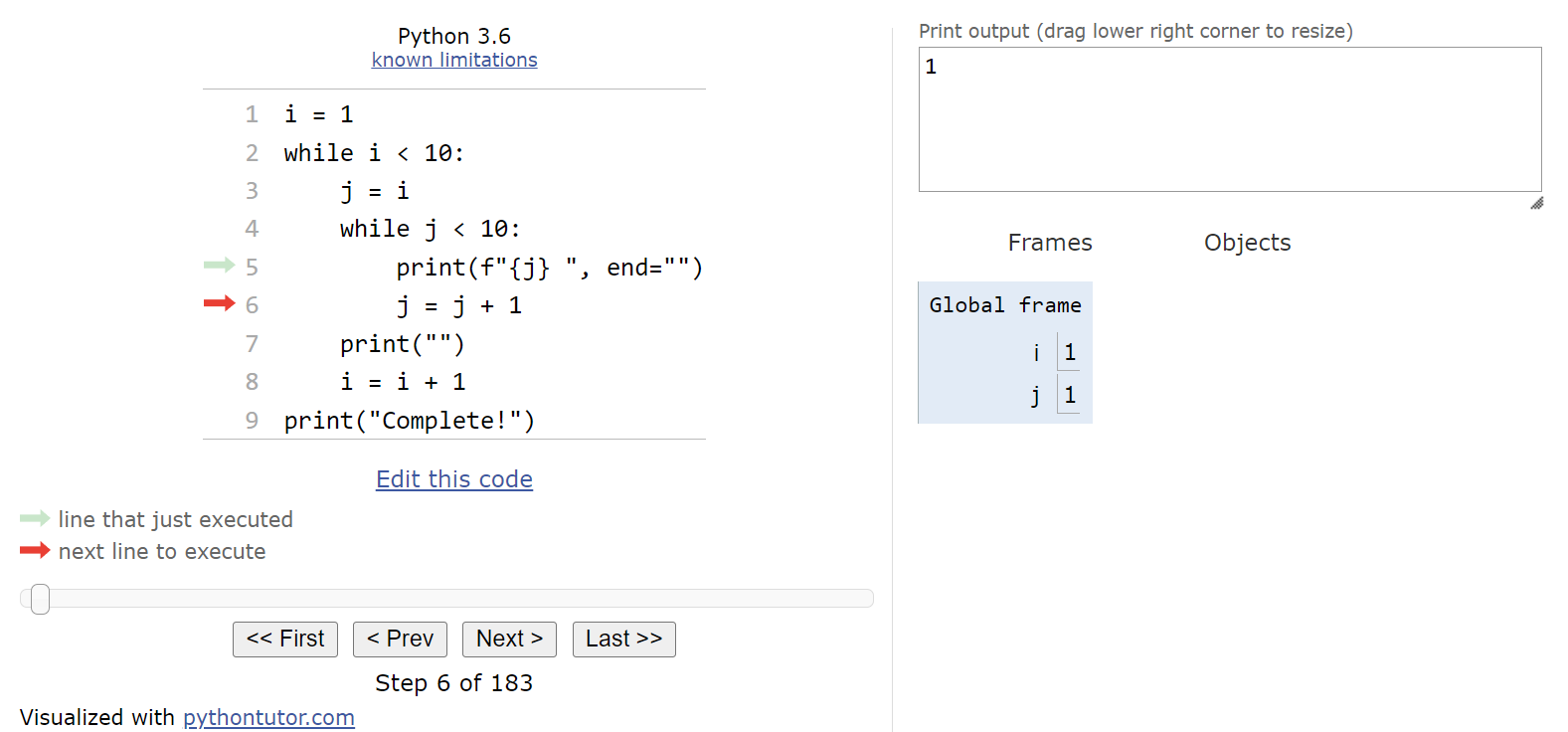
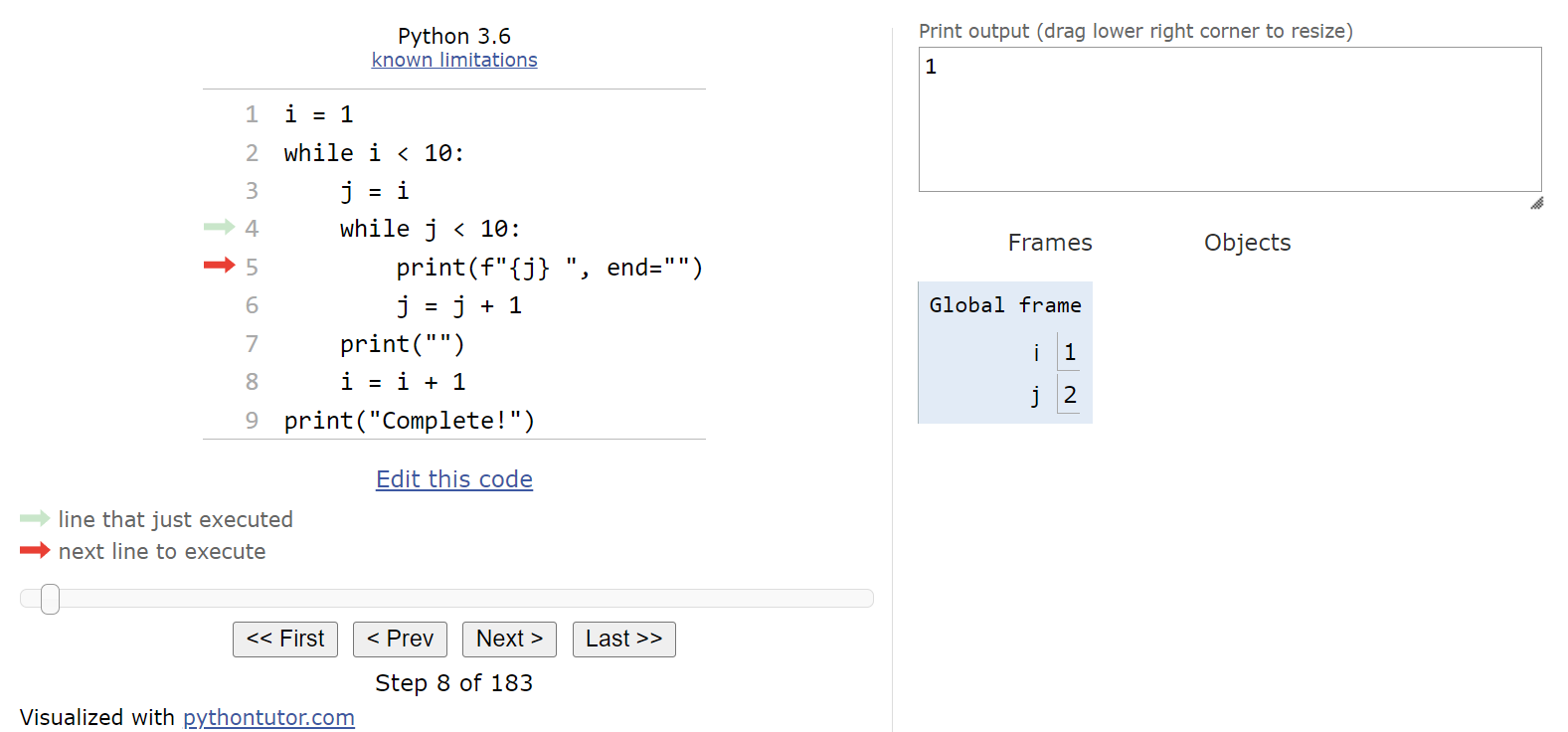
Inside of the inner while loop, we’ll perform two actions. First, we’ll print the current value of j to the output, but we won’t move to the next line since the end parameter is set to an empty string in the print() function:
Then, we’ll increment the value of j by $1$ before looping back to the top of the innermost loop:
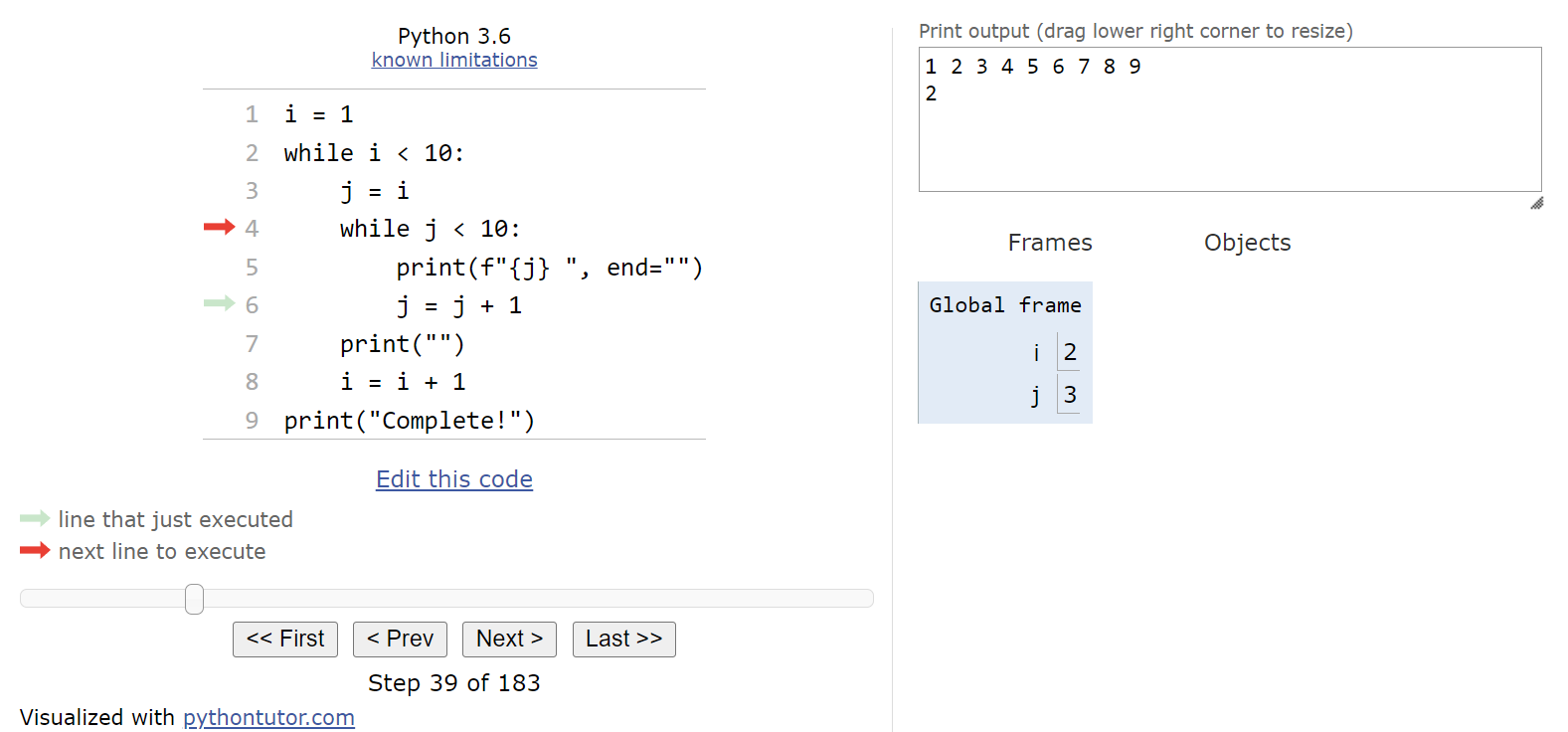
Notice that when we reach the end of the innermost loop, we jump back to the beginning of that loop, NOT to the beginning of the outermost loop. This is an important concept to learn - since we are only dealing with the inner loop at this point, we must continue to repeat its steps until the Boolean expression evaluates to False. So, since the Boolean expression j < 10 still evaluates to True, we should enter the loop once again.
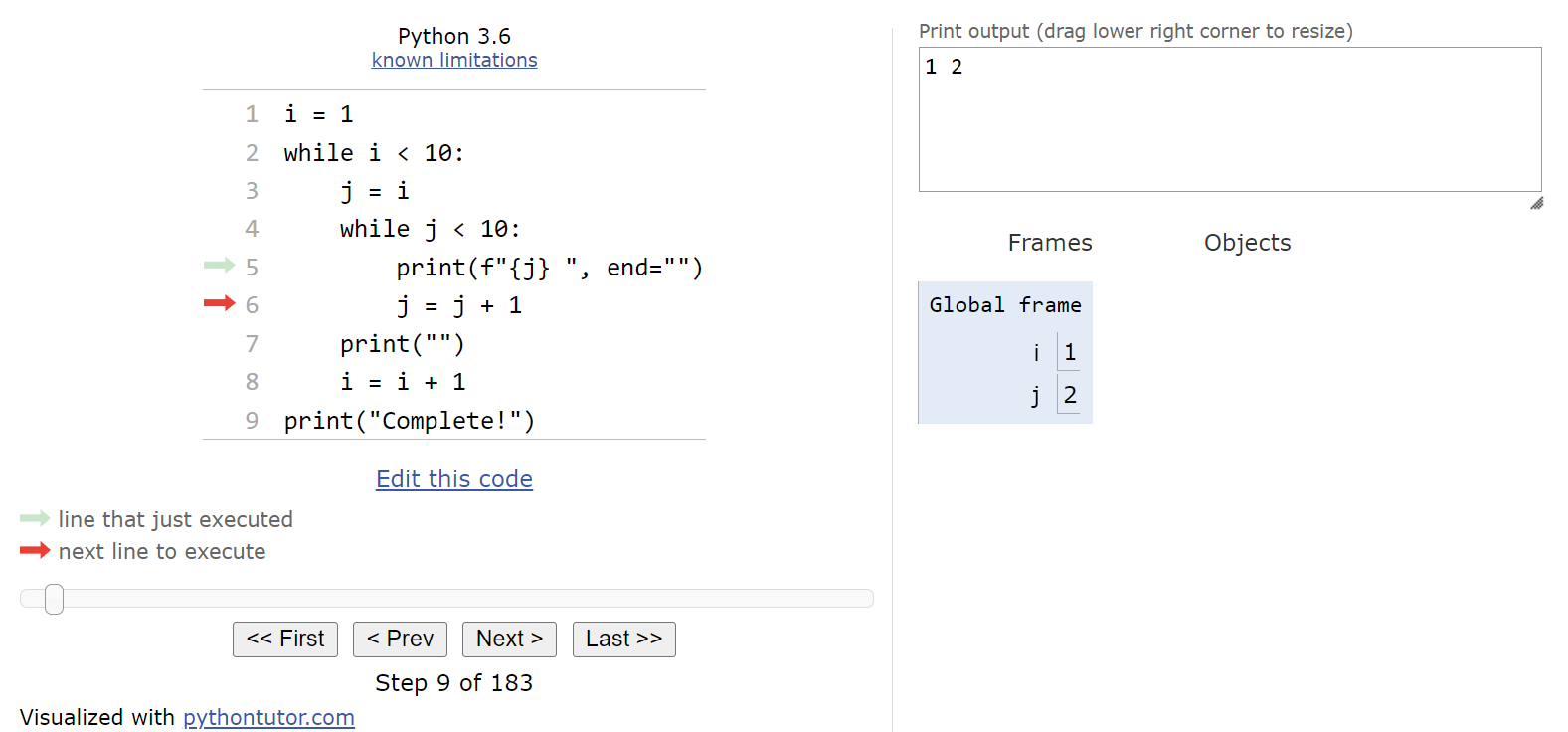
Inside the loop, we’ll print the current value of j to the same line of output as before:
And once again we’ll increment the value of j by $1$ and jump back to the top of the innermost while loop:
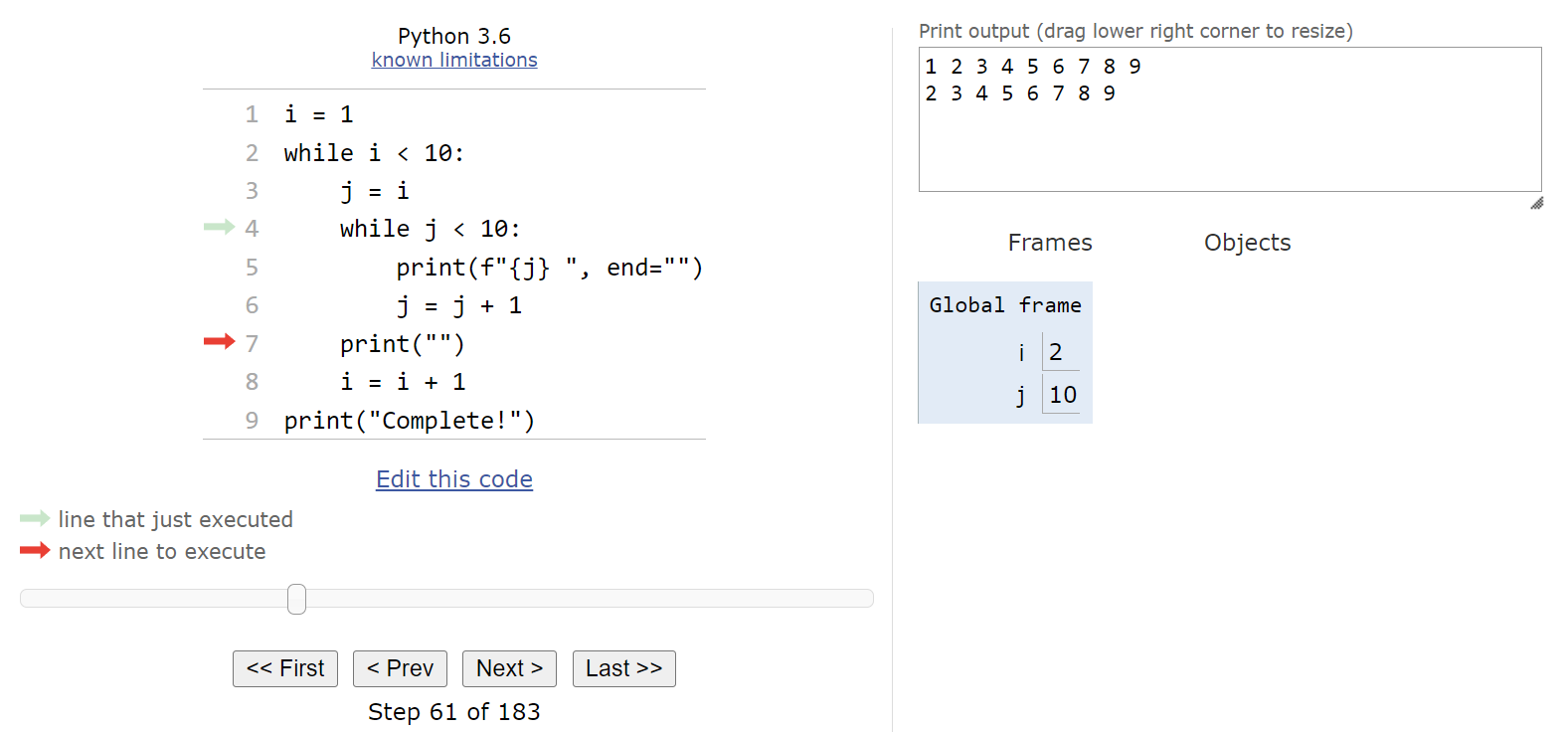
Hopefully at this point we have a pretty good idea of what each step of the innermost while loop does. It will simply print the value of j and increment it by $1$, repeating those steps until j is greater than or equal to $10$. So, once the inner while loop terminates, we’ll see this state:
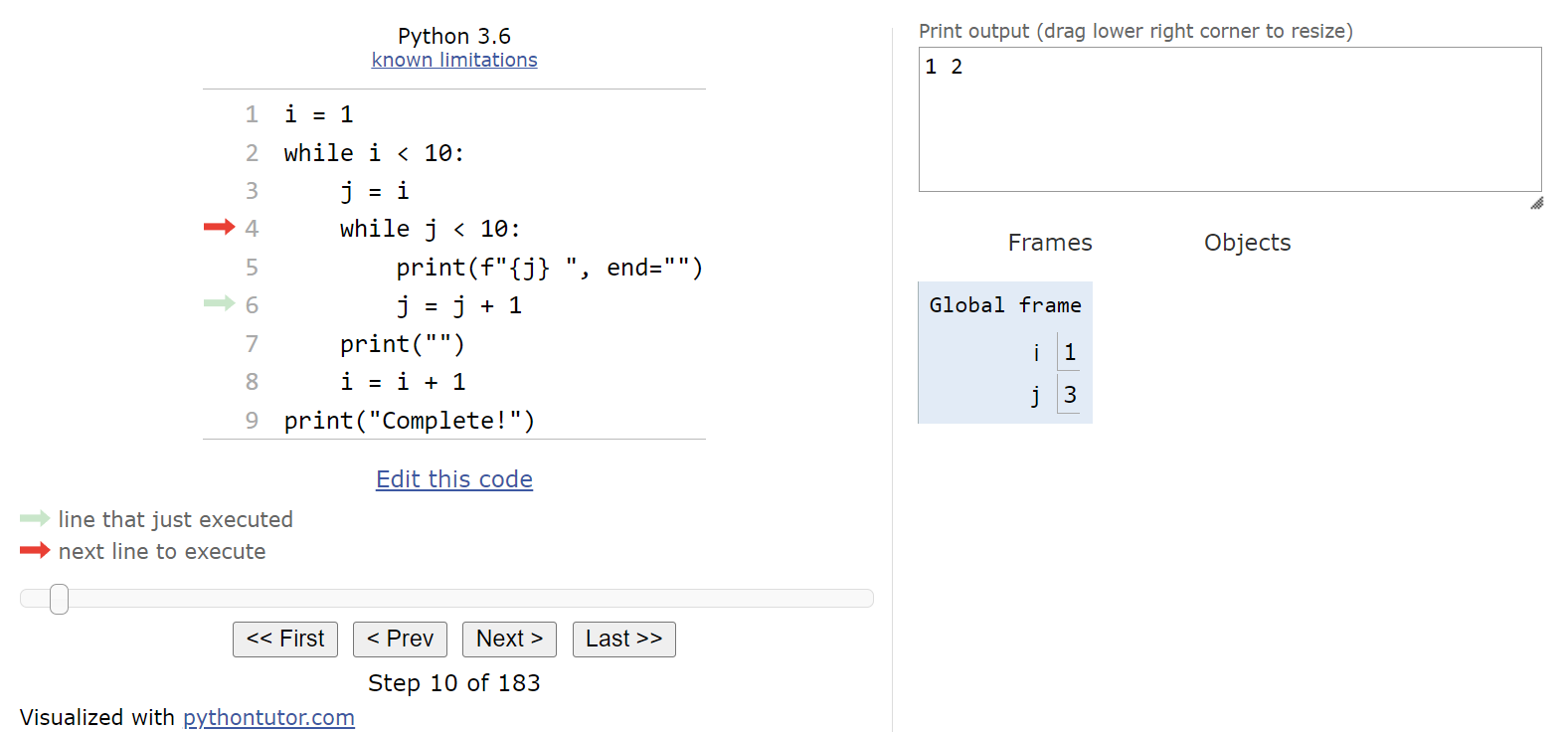
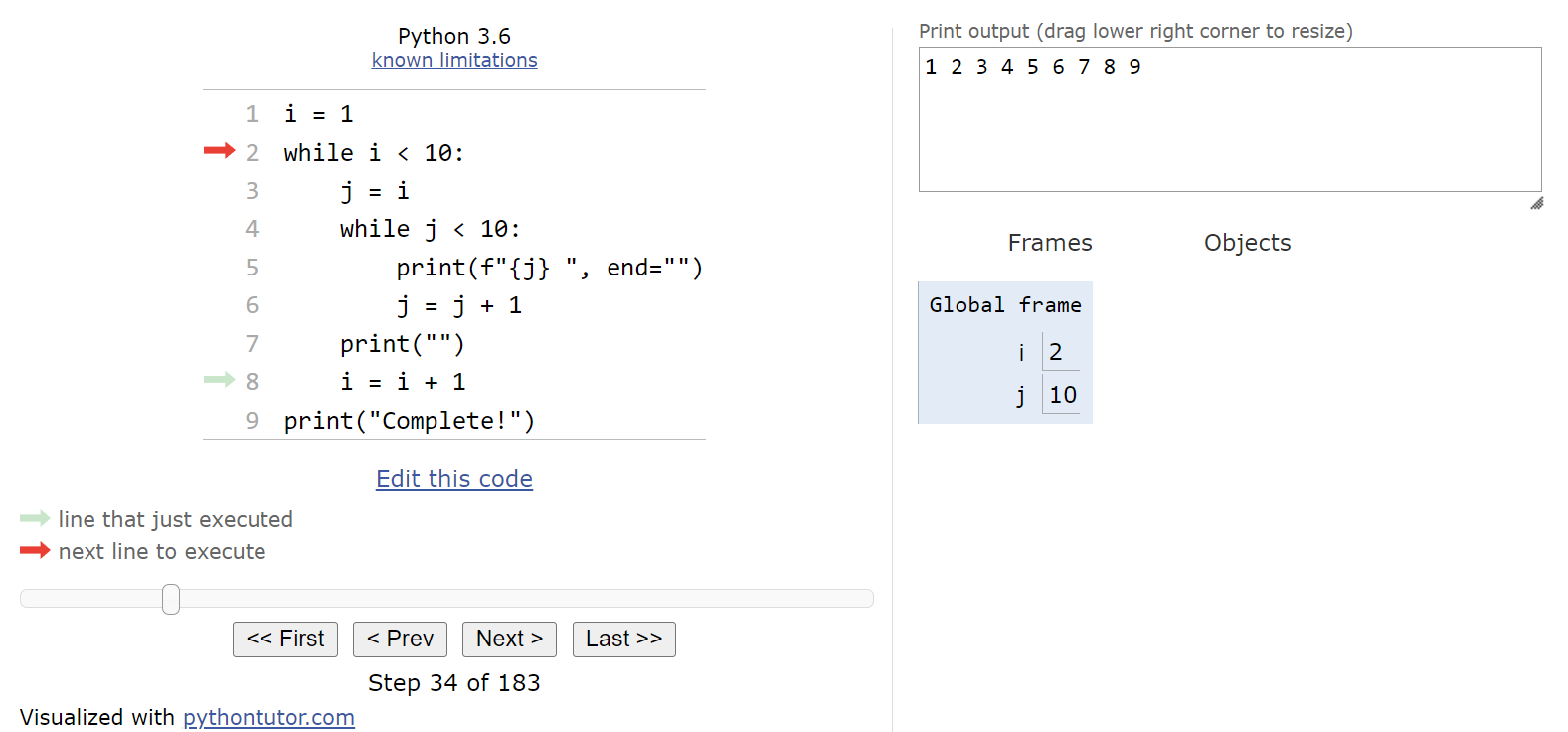
We jumped from step 10 to step 32 just to complete the inner while loop. Finally, at this point we’ll print an empty string, which will move our output to the next line, and then we’ll increment the value in i by $1$ before looping to the top of the outer while loop:
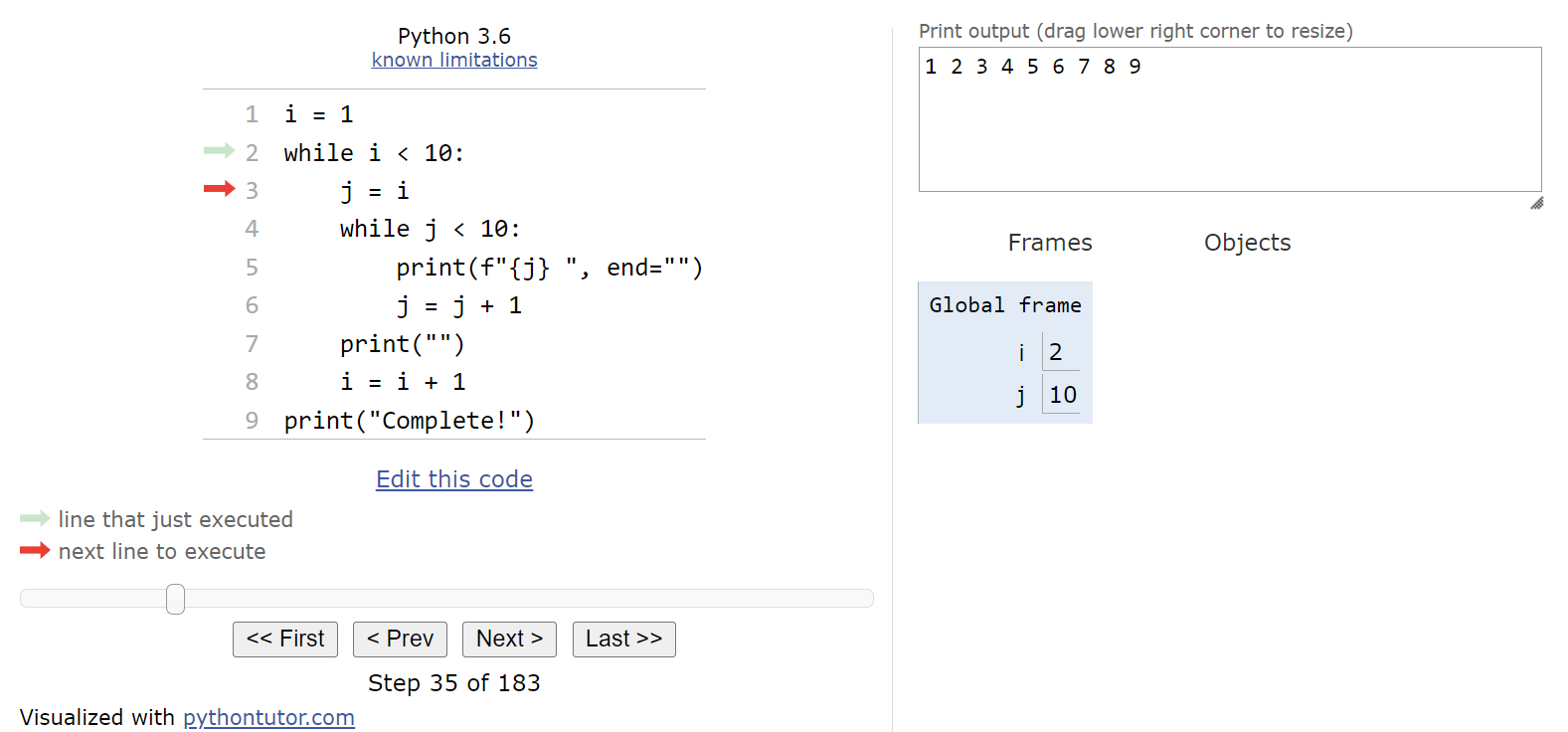
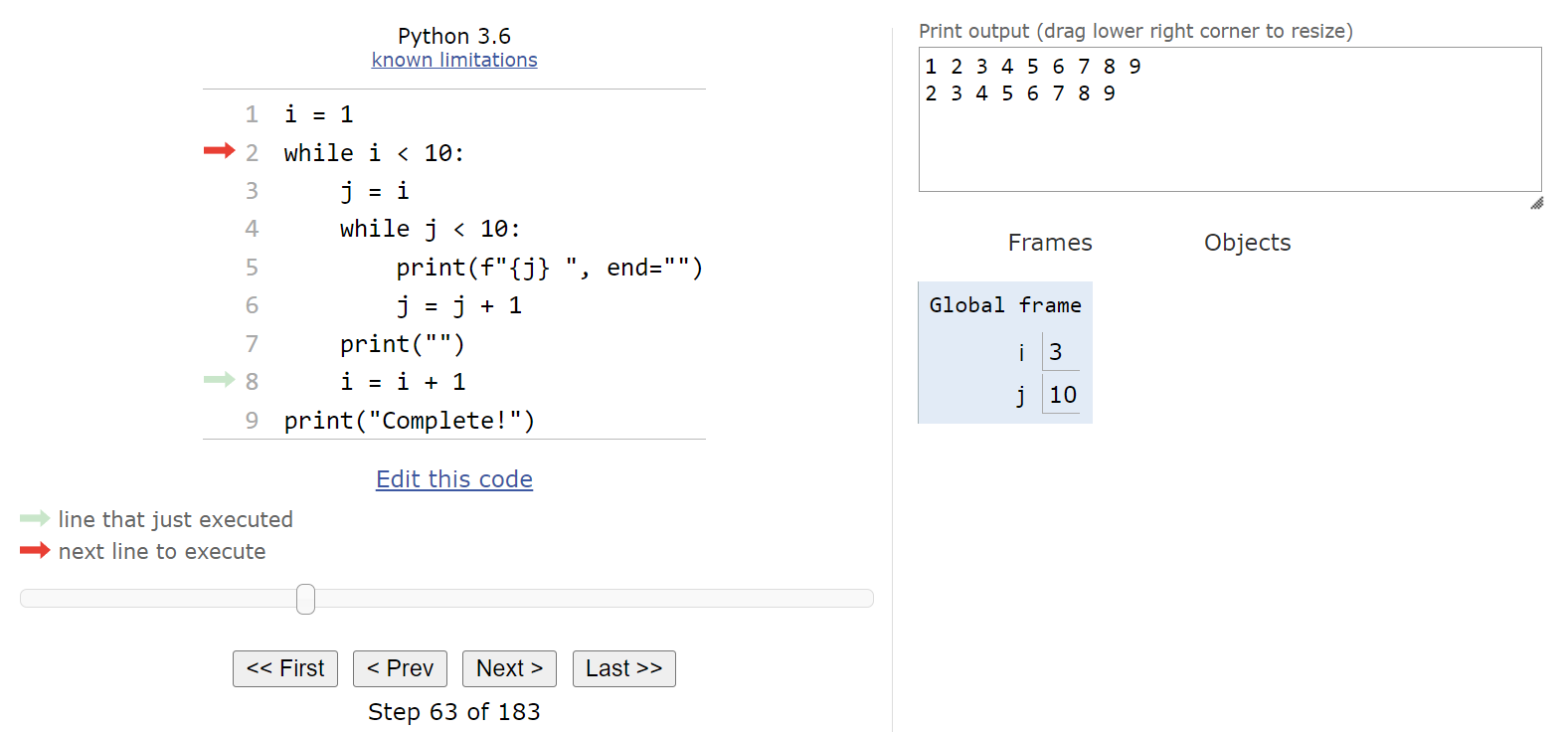
Now we must check to see if we should enter the outer while loop again by checking the Boolean expression i < 10. Since that evaluates to True, we’ll enter the loop a second time.
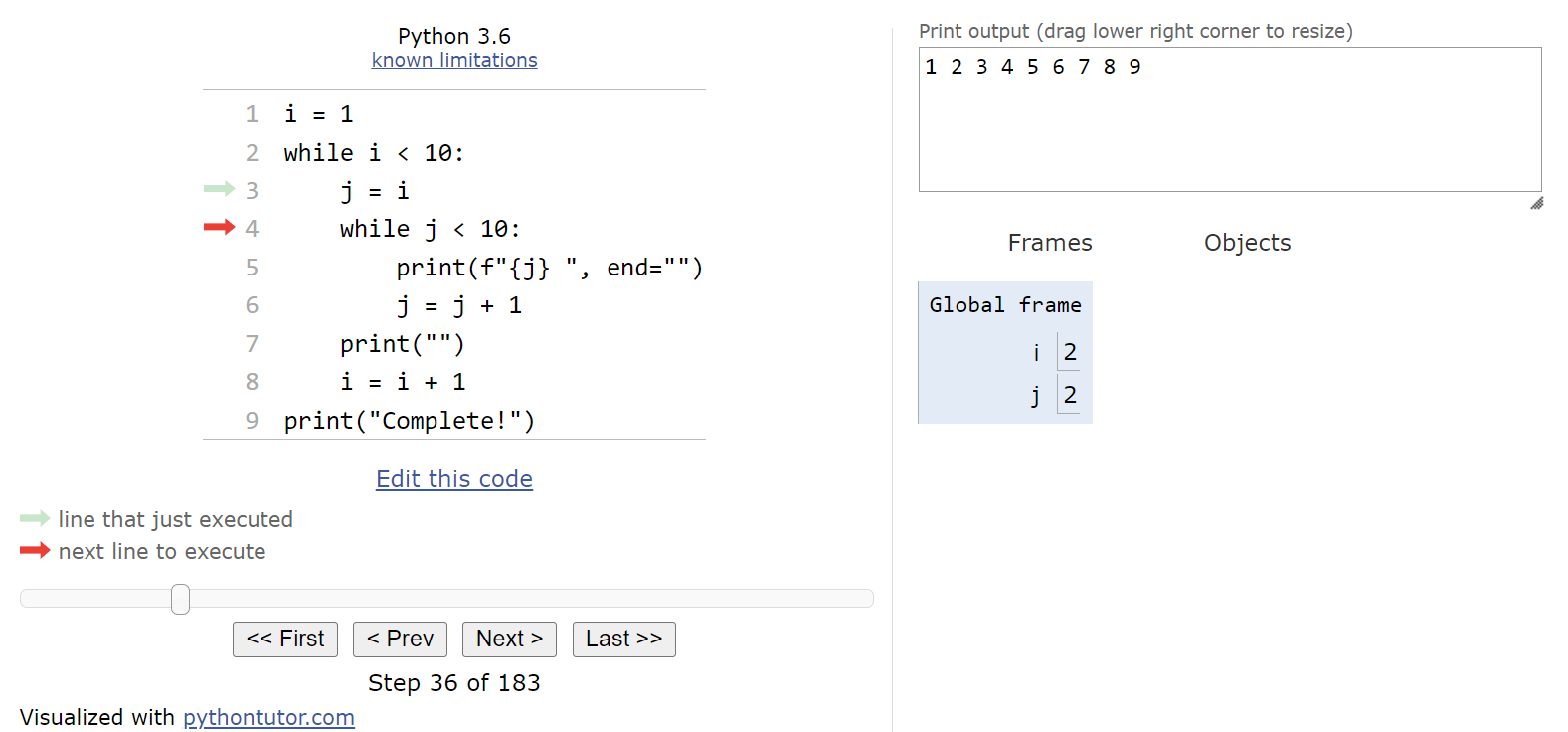
Inside the loop, we’ll reset the value of j to be the current value stored in i, which is now $2$, and then we’ll reach the inner while loop:
Here, we can evaluate the Boolean expression j < 10, which is currently True, and determine that we should enter the inner while loop.
Inside the loop, the code hasn’t changed, so we can use our understanding from before to quickly figure out what this loop does. It will print the current value in j and then increment j by $1$, so we’ll end up at this state:
At this point, we can easily assume that the inner loop will do pretty much the same thing as before - it will print all of the values from i up through $9$ to the output, all on the same line. So, once the inner loop has completely finished, we’ll see the following state in Python Tutor:
We were able to quickly jump from step 42 all the way to step 64 just by understanding what the inner loop is doing and extrapolating from our previous experience. Now, we can finish up this iteration of the outer loop by printing a newline and then incrementing i by $1$, and then we’ll be back at the beginning of the outer while loop:
At this point, we’ve completely worked through two iterations of the outermost while loop, including two complete executions of the innermost while loop. So, we’re at a good point to make a prediction about the output of the program as a whole, without executing the next 120 steps. It looks like the inner loop will print the values from i through $9$ on a single line, and then each line will start with the value of i being incremented by $1$ each time. So, overall, we can expect the entire outer while loop to produce the following output:
1 2 3 4 5 6 7 8 9
2 3 4 5 6 7 8 9
3 4 5 6 7 8 9
4 5 6 7 8 9
5 6 7 8 9
6 7 8 9
7 8 9
8 9
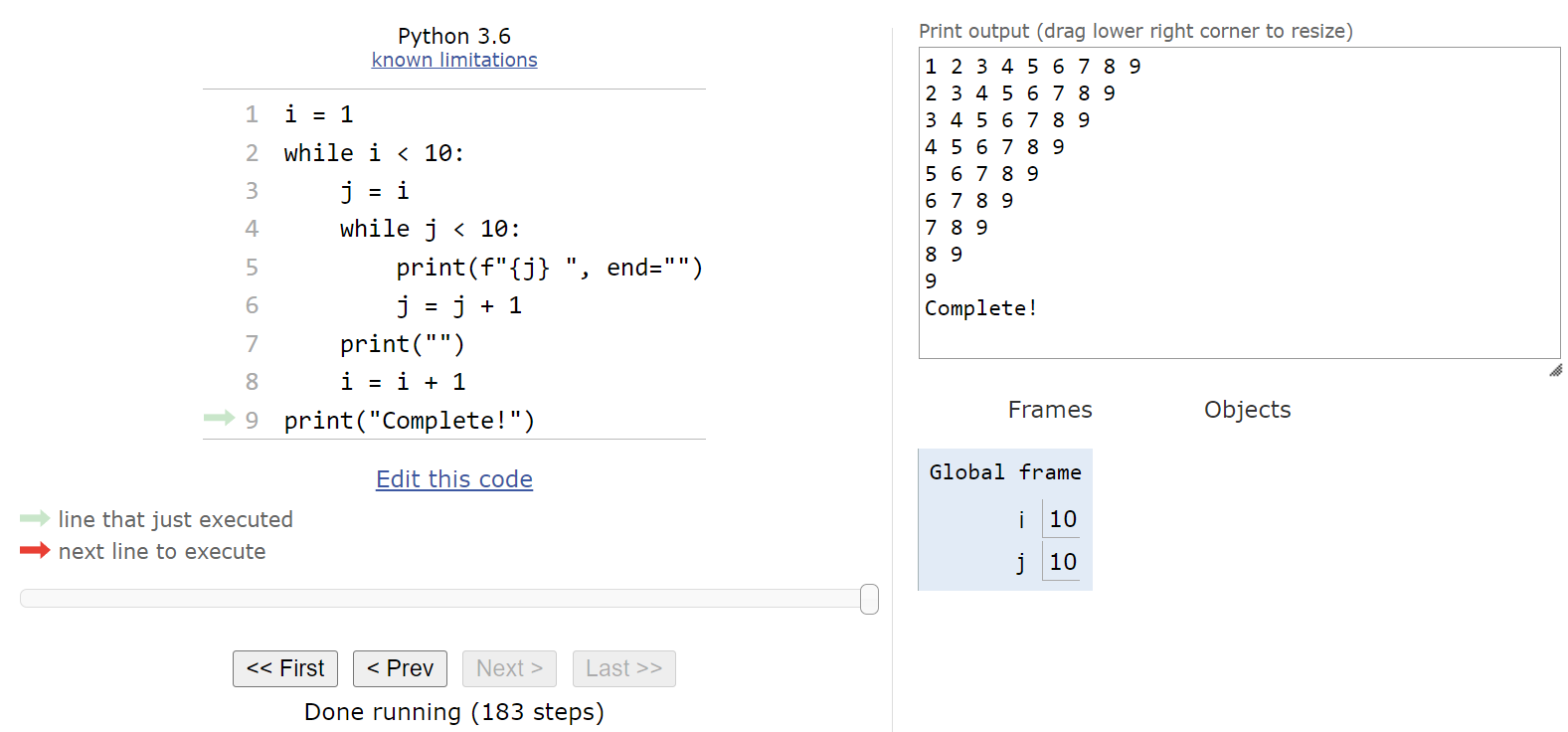
9And, indeed, if we jump ahead to the last line of the program we’ll see exactly that situation in Python Tutor:
The program ends by printing the string "Complete!". At the end of the program, we’ll see the following state:
Working through an example program such as this one is a great way to explore how nested loops work in Python
Tips for Nested Loops
Writing code that has nested while loops can be quite tricky, as there are several pitfalls that we might encounter. Here are a few tips to keep in mind when designing code that uses nested while loops:
- Try to understand the relationship between each loop’s Boolean expression. If possible, use different variables in each one. It is easy to write code where the Boolean expressions are closely related, causing an infinite loop to occur.
- Look for ways to combine the nested loops into a single loop if possible. While this may not always be an option, it can make reasoning about the code much simpler.
- Try to make the loops as simple as possible. It is much easier to debug loops that use a simple iterator that increments regularly instead of a complex Boolean expression. Likewise, try to build loops that either both increment or both decrement the iterator variable to maintain consistency.
Nested loops present a very difficult challenge for programmers, because they are short snippets of code that may end up resulting in hundreds or even thousands of individual steps to be executed. So, anything we can do to make the loops simpler and easier to understand will greatly improve our ability to write programs with fewer bugs.
Subsections of Nested While Loops
Nested For Loops
YouTube VideoResources
For loops can also be nested, just like while loops. In fact, nesting for loops is often much simpler than nesting while loops, since it is very easy to predict exactly how many times a for loop will iterate, and also because it is generally easier to determine if a for loop will properly terminate instead of a while loop.
A great way to explore using nested for loops is by printing ASCII Art shapes. For example, consider the following Python program that contains nested for loops:
for i in range(3):
for j in range(5):
print("* ", end="")
print("")Just by looking at the code, can you predict what shape it will print? We can check the result by running the program on the terminal directly. If we do so, we should receive this output:
* * * * *
* * * * *
* * * * * It printed a rectangle that is $ 3 $ rows tall (the outer for loop) and $ 5 $ columns wide (the inner for loop). If we look back at our code, this hopefully becomes very clear. This is a very typical structure for nested for loops - the innermost loop will handle printing one line of data, and then the outer for loop is used to determine the number of lines that will be printed.
The process for dealing with nested for loops is nearly identical to nested while loops. So, we won’t go through a full example using Python Tutor. However, feel free to run any of the examples in this lab in Python Tutor yourself and make sure you clearly understand how it works and can easily predict the output based on a few changes.
Example 1
Let’s look at a few more examples of nested for loops and see if we can predict the shape that is created when we run the code.
for i in range(5):
for j in range(i + 1):
print("* ", end="")
print("")This time, we’ve updated the inner for loop to use range(i + 1), so each time that inner loop is reached, the range will be different based on the current value of i from the outer loop. So, we can assume that each line of text will be a different size. See if you can figure out what shape this will print!
When we run the code, we’ll get this output:
*
* *
* * *
* * * *
* * * * * We see a triangle that is
$ 5 $ lines tall and
$ 5 $ columns wide. If we look at the code, we know that we’ll have 5 rows of output based on the range(5) used in the outer loop. Then, in the inner loop, we can see that the first time through we’ll only have a single item, since i is
$ 0 $ and the range used is range(i + 1).
The next iteration of the outer loop will have
$ 1 $ stored in i, so we’ll end up repeating the inner loop
$ 2 $, or i + 1, times. We’ll repeat that process until the final line, which will have
$ 5 $ characters in it to complete the triangle.
From here, we can quickly modify the program to change the structure of the triangle. For example, to flip the triangle and make it point downward, we can change the range in the inner loop to range(i, 5) instead!
Example 2
What if we want to flip the triangle along the vertical axis, so that the long side runs from the top-right to the bottom-left? How can we change our nested loops to achieve that outcome?
In that case, we’ll not only have to print the correct number of asterisks, but we’ll also need to print the correct number of spaces on each line, before the asterisks. One possible way to achieve this is shown in this code:
for i in range(5):
for j in range(4 - i):
print(" ", end="")
for j in range(i + 1):
print("* ", end="")
print("")Here, we have two for loops nested inside of our outer loop. The first loop creates a range using the expression 4 - i, and the second loop uses the expression i + i. So, when i is equal to
$ 0 $ during the first iteration of the outer loop, the first inner loop will be executed
$ 4 $ times, and the second loop only
$ 1 $ time. Then, on the next iteration of the outer loop, the first inner loop will only run
$ 3 $ times, while the second loop now runs
$ 2 $ times. Each time, the sum of the iterations will be
$ 5 $, so our lines will always be the same length.
When we run the code, we’ll get this output:
*
* *
* * *
* * * *
* * * * * Example 3
Up to this point, we’ve just been writing loops to print shapes using ASCII art. While that may seem trivial, understanding the “shape” that will be produced by a given set of nested loops can really help us understand how the code itself will function with other data.
Consider this example code:
total = 0
count = 0
for i in range(10):
for j in range(i + 1):
total = total + (i * j)
count += 1
print(f"sum: {total}, count: {count}")
main()Before we even try to run this code, can we guess what the final value of the count variable will be? Put another way, can we determine how many times we’ll execute the code in the innermost loop, which will help us understand how long it will take for this program to run?
Let’s compare this code to the first example shown above:
for i in range(5):
for j in range(i + 1):
print("* ", end="")
print("")Notice how the code structure is very similar? The outermost loop runs a given number of times, and then the inner loop’s iterations are determined by the value of the outer loop’s iterator variable. Since we know that the second example produces a triangle, we can guess that the program above runs in a similar way. So, the first iteration of the outer loop will run the inner loop once, then twice on the second iteration, and so on, all the way up to $ 10 $ iterations. If we sum up all the numbers from $ 1 $ to $ 10 $, we get $ 55 $.
Now let’s run that code and see if we are correct:
As this example shows, we can use our basic understanding of various looping structures to help us understand more complex programs, and even predict their output without running or tracing the program. This is a very useful skill to learn when working with nested loops.
Subsections of Nested For Loops
Testing Nested Loops
YouTube VideoResources
Testing nested loops can also be very tricky, especially because they can make our program’s control flow even more complex. So, let’s briefly go through an example to see how to determine what inputs we can use to test nested loops.
Consider the following example program:
x = int(input("Enter a positive integer: "))
while x <= 0:
print("Invalid input!")
x = int(input("Enter a positive integer: "))
y = int(input("Enter a positive integer: "))
while y <= 0:
print("Invalid input!")
y = int(input("Enter a positive integer: "))
while y <= x:
for i in range(x - y):
print("*", end="")
y = y + 2
print("")
print("Complete!")Let’s work through the process of generating some test cases for this program to see if it runs without any errors. As always, our biggest concern is to make sure that we don’t reach a situation where the program enters an infinite loop, and that we also try to provide inputs that will enter each loop at least once, and also bypass each loop if possible.
Input Loop
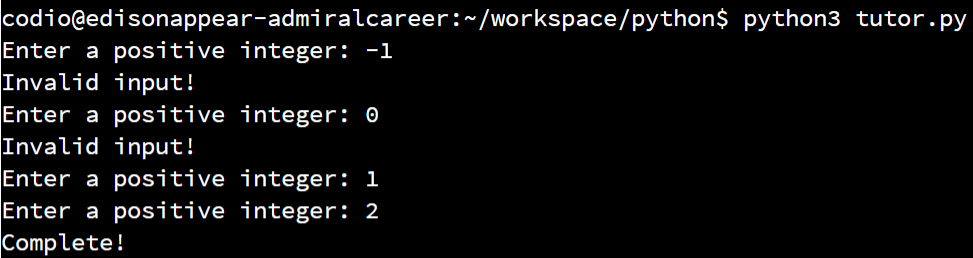
First, we see that the code uses a loop twice to make sure the user inputs only positive values. So, some of our first test cases could involve trying values such as $ -1 $, $ 0 $ and $ 1 $ to check the edge cases of that while loop’s Boolean expression. When we run the program and provide those inputs, we should see it enter the loop in that function at least once.
We can also bypass that loop by simply making sure we enter a positive integer each time. So, we know we have a few test cases available that will achieve branch coverage for that loop.
Outer While Loop
Next, let’s consider the outermost while loop after the input loops. That loop uses the Boolean expression y <= x to determine if the loop should be entered or not. So, we want to come up with a few tests that check the edge cases of that Boolean expression. We can start by choosing a value to use for x, such as
$ 5 $. Then, the edge cases of that Boolean expression would be when y is either
$ 4 $,
$ 5 $, or
$ 6 $.
If y is
$ 6 $, the Boolean expression would be False and it should bypass the loop. We can easily test this to make sure that is the case:
Likewise, if y is
$ 4 $, we know that it should enter the outermost loop. Inside, we see a for loop that will iterate based on the expression x - y. Effectively, it will compute the difference between x and y and then iterate that many times. So, if x is
$ 5 $ and y is
$ 4 $, the difference between those values will be
$ 1 $. So, we’ll enter the innermost for loop at least once. When we run the program with these inputs, we’ll see the following output:
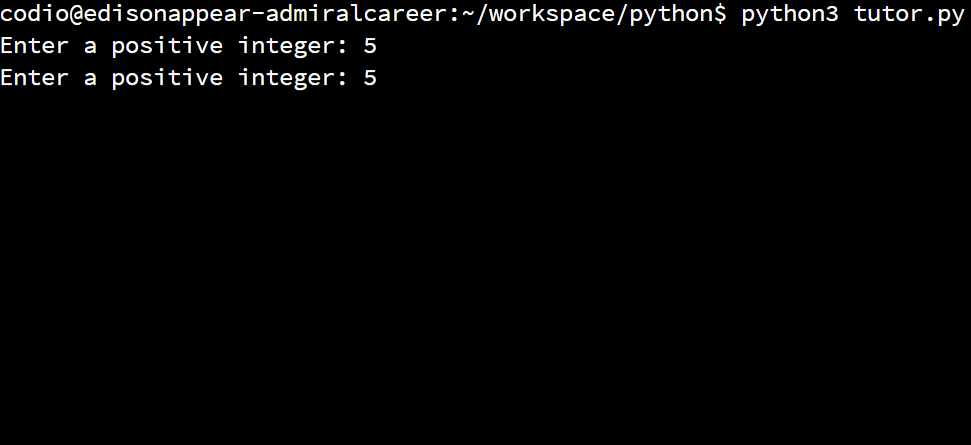
What if we set both x and y to be the same value? We know that the inner for loop will run x - y times, so if both x and y are the same value, this would be a way to bypass that loop, while still entering the outermost while loop since y <= x will be True. However, when we try to run the program with these inputs, we’ll see something interesting happen:
Our program will quickly start printing blank lines of output to the terminal. So quickly, in fact, that it is hard to even see what happens. As it turns out, we accidentally caused our program to enter an infinite loop! When this happens, the only way to stop the program is to close the terminal window it is running in, or use the CTRL+C keyboard command to interrupt it. So, let’s see why this infinite loop is occurring, and figure out how we can fix it.
Infinite Loop
Did you spot the infinite loop when you first read the program’s code? It can be really tricky to find, which is why we have to be very good about choosing test cases that will explore many different ways to run the program.
In this case, the infinite loop is caused by the interaction between the two loops. In the outermost while loop, we have the Boolean expression y <= x to enter the loop. However, inside that loop, the for loop will only execute x - y times, which also happens to be the loop variant for the outer while loop. The key to the infinite loop lies in the fact that the only line inside of the outer while loop that will change the value of either x or y is also inside of the inner for loop. So, if we don’t execute the for loop’s code at all, then the value of x and y won’t change either, and we’ll continually repeat the steps of the outermost while loop.
There are many ways to fix this problem, but the simplest would be to change the Boolean expression of the outermost while loop to be y < x. That will ensure that there is at least one iteration of the innermost for loop, and the infinite loop condition will be avoided.
So, as this example shows, testing nested loops is just like testing regular loops - we want to try and find inputs that will enter the loop at least once, as well as inputs that will bypass the loops if possible, just to make sure there aren’t any strange situations that may arise. While this won’t find all errors that are present in code containing nested loops, it is a great way to start testing your programs.
Subsections of Testing Nested Loops
Worked Example
YouTube VideoResources
Now that we’ve explored how to create programs that contain nested loops, let’s work through a complete example problem to see how we can convert a problem statement into working code.
Consider the following problem statement:
Write a program to print the sum of the first
nprime numbers, wherenis provided as input from the user.
This is a very simple problem statement, but it can be very complex to build a program that satisfies it. So, let’s go through the steps and see if we can get it to work.
Handling User Input
The first thing we’ll need to do is get input from the user, since we really can’t do anything else until we know what our goal is. While the problem statement doesn’t include any information about what inputs are acceptable, we can infer that only positive integers should be used as input. So, we can borrow the loop for input from earlier in this module to handle all of our input:
x = int(input("Enter a positive integer: "))
while x <= 0:
print("Invalid input!")
x = int(input("Enter a positive integer: "))
n = xReusing existing code, such as the loop for input we just included here, is a great way to build our programs. We can always think of previous code that we’ve already written and tested as possible building blocks for future programs, and reusing existing code is a great way to speed up our development process.
Prime Numbers
Next, we need some way to determine if a number is a prime number. Recall from mathematics that a prime number is a number that is only equally divisible by $ 1 $ and itself. For example, $ 7 $ is prime, but $ 8 $ is not since it can be evenly divided by $ 4 $.
Thankfully, we know that we can use the modulo operator % to determine if a number if evenly divisible by another number. So, all we need to do is check if each number less than our chosen number can equally divide it. If none of them can, then our chosen number is prime.
So, let’s write code that performs this operation. We know that we need to check all of the numbers from
$ 2 $ up to but not including x. We can do this using a for loop and the range() function:
for i in range(2, x):Inside of the for loop, we want to check and see if the iterator variable i can evenly divide the chosen number n using the modulo operator:
for i in range(2, x):
if x % i == 0:
# i equally divides xHere’s where things get a bit tricky - if i can equally divide x, we know that x is not prime. So, let’s add a Boolean value to keep track of this. We’ll set it initially to True before the loop, and then we can set it to False as soon as we know the number is not prime:
is_prime = True
for i in range(2, x):
if x % i == 0:
is_prime = False
# what if we get here?We might realize that we don’t have to check any other values once we have determined that x is not prime. So, in our code, we can just use the break statement to end the loop early and go to the next part of the code. In effect, we can use this to shortcut the rest of the loop.
is_prime = True
for i in range(2, x):
if x % i == 0:
is_prime = False
break
# what if we get here?We don’t introduce the break and continue statements in this class just to simplify things, but you are welcome to use them if you understand them.
However, what happens if we check all of the values from
$ 2 $ up to x and don’t find a single one that will equally divide our chosen number x? In that case, we’ll reach the end of our for loop, and is_prime will still be True. So, we’ve confirmed that x is indeed a prime number!
is_prime = True
for i in range(2, x):
if x % i == 0:
is_prime = False
# is_prime stores whether nx is prime or notThere we go! That’s a quick and easy way to determine if a given number is prime. This is a great example of a pattern that we’ll see many times as we write complex programs whenever we must determine if a particular situation is true for a given list of numbers. Inside of the loop, we’ll check each case and set a value to False if it isn’t true. If it is true, then we’ll complete the entire loop without setting that value to False, so we’ll know that it is True at the end of the code. We’ll see this pattern again in a later lab.
The code above is very simple, but not very efficient. With a bit of thought, it is easy to determine that we only have to actually check numbers up to x /2, since it is impossible for any number larger than that to evenly divide x. Likewise, we can do some quick math to eliminate numbers that end in an even digit or
$ 5 $, since those numbers will never be prime.
Finally, we could use a more advanced mathematical technique such as the Sieve of Eratosthenes to generate all prime numbers more quickly. However, for this example, we’ll stick to the simplest approach.
Complete Program
Finally, now that we have the code to determine if a number is prime, we can complete our program by simply iterating through all possible numbers until we’ve found n prime numbers, and then print the sum:
x = int(input("Enter a positive integer: "))
while x <= 0:
print("Invalid input!")
x = int(input("Enter a positive integer: "))
n = x
count = 0
x = 2
total = 0
while count < n:
is_prime = True
for i in range(2, x):
if x % i == 0:
is_prime = False
if is_prime:
total = total + x
count = count + 1
x = x + 1
print(f"The sum of the first {n} prime numbers is {total}")This program requires three additional variables. The variable count is used to keep track of the number of prime numbers found, so we’ll increment it inside of the if statement each time we find a prime number. Likewise, the total variable keeps track of the sum of the prime numbers, which we’ll print at the end. Finally, we use x as our iterator variable, so we must make sure that we increment x each time the while loop iterates, outside of the if statement. We’ll start x at
$ 2 $, since
$ 1 $ is not a prime number mathematically. A very common programming mistake is to forget to increment x outside the if statement, resulting in an infinite loop. Also, we chose to use a while loop instead of a for loop since our program’s goal is to sum up the first n prime numbers, which is better expressed as a while loop instead of a for loop.
Feel free to run this program in Python or using Python Tutor to confirm that it works as expected before continuing.
Testing
Testing this program is a bit complex, since we can only provide a single input. We can easily provide a negative value or $ 0 $ to confirm that the loop handling input is working correctly, but beyond that we have little control over the rest of the program just by changing inputs.
Instead, we have to rely on our ability to read and analyze the code to determine if it is working properly. For example, we can look at the second loop in the main part of the code. It is a while loop, which relies on the count variable increasing until it is greater than or equal to n before it will terminate. We can see that count will be incremented each time the value of x is prime, so as long as we are able to find enough prime numbers, and assuming our code to check prime numbers works correctly, this loop should eventually terminate.
In the code to check if a number is prime, we have a simple for loop, which will always terminate eventually. There is no way to bypass it, so we don’t really have to worry about that code not eventually terminating.
However, proving that this program creates the correct answer is a bit trickier. One of the best ways to do this is to simply check a few answers manually. For example, with a bit of searching online, we can find a list of prime numbers. According to Wikipedia, the first 9 prime numbers are:
2
3
5
7
11
13
17
19
23The sum of those numbers is easy to calculate using a calculator or other device, and eventually we can be fairly certain that the correct answer is $ 100 $. When we run our program, we should hopefully get the same result:
We can test a few other numbers until we are sure that our program is working correctly.
Hopefully this example is a good look at how to build a program using loops that meets a given problem description. We were able to put together various types of loops and conditional statements in our program, and then test it to be sure it works. As you continue to work on projects in this class, feel free to refer back to these examples for ideas and blocks of code that you may want to use in your own programs. Good luck!
Subsections of Worked Example
Nesting Practice
Let’s try some simple practice problems. These problems are not graded - they are just for you to practice before doing the real exercises in the lab itself. You can find the answers below each question by clicking the button below each question.
5.7 Reading Code
Consider the following Python program:
x = int(input("Enter a positive integer: "))
while x <= 0:
print("Invalid input!")
x = int(input("Enter a positive integer: "))
n = x
for i in range(n - 1):
for j in range(n - i - 1):
print(" ", end="")
for j in range(i + 1):
print("* ", end="")
print("")
for i in range(n):
for j in range(n):
print("* ", end="")
print("")Describe the shape that will be printed when this program is executed. Try to do so without running the code directly, but feel free to check your answer after guessing.
5.8 Debugging Code
Consider the following Python program:
x = 3
y = 5
while x => 0:
for i in range(y):
print("* ")
print("")
x = x + 1This code is supposed to print a rectangle of asterisks that is x rows tall and y columns wide. However, it contains multiple syntax and logic errors preventing it from working correctly. Describe how to fix the errors in the given code to produce the desired output.
5.9 Writing Code
Write a complete Python program in that file that meets the specification below.
Write a program that will print a Parallelogram of asterisks that is m rows tall and n columns wide, where the topmost row is furthest toward the left. The values m and n should be provided by the user as input. If the user inputs a value that is
$ 0 $ or negative, the program should print an error and prompt for input again.
For example, if the user inputs $ 3 $ and $ 5 $, the program should provide the following output:
* * * * *
* * * * *
* * * * * Notice that each asterisk is separated by a space, and each successive row of the parallelogram begins one space to the right of the previous row.
Summary
In this lab, we introduced several major important topics in Python. Let’s quickly review them.
Python While Loops
While loops in Python will execute while a Boolean expression evaluates to true.
while <boolean expression>:
<block of statements>Range Function
The range() function in Python is used to generate a list of numbers. It can be used in three ways:
range(stop)- numbers from $0$ up to (but not including)stoprange(start, stop)- numbers fromstartup to (but not including)stoprange(start, stop, step)- numbers fromstartup to (but not including)stop, withstepbetween each number.
Python For Loops
For loops in Python will execute a set number of times.
for <iterator variable> in <list>:
<block of statements>Input with Loops
Loops can be used to request new input from the user if invalid input is received.
x = float(input("Enter a percentage as a decimal number from 0 to 1: "))
while(x < 0 or x > 1):
print("Invalid Input!")
x = float(input("Enter a percentage as a decimal number from 0 to 1: "))Testing Loops
Loops can be tested for both branch and path coverage. In general, achieving path coverage involves writing code that will enter the loop, and also code that will bypass the loop entirely.
Loops should also be tested for termination and situations that may result in infinite loops. Using a loop variant and showing that it is monotonically decreasing is a helpful technique.
Nested Loops
Loops in Python can be nested, just like any other statement. While loops and for loops can be nested in any combination.
Testing Nested Loops
When testing nested loops, it is important to consider situations where a loop will be executed and where it will be bypassed. It is also important to consider the loop variants for while loops to ensure that there aren’t situations where a loop will accidentally run infinitely.
Efficiency
Nested loops can result in programs that execute many individual steps, even using just a few lines of code. It is always helpful to think about the number of times a loop will execute and make sure that it isn’t executing more times than necessary.