Worked Example
YouTube VideoResources
Finally, let’s work through another full example program in Python that uses lists and strings, just to gain some more experience with the various ways we can use the techniques we’ve learned in this lab.
For this example, consider the following problem statement:
Write a program to construct and print Pascal’s Triangle for a given number of rows. The user should be prompted to enter a positive integer indicating the number of rows, and if the user provides an invalid input the program should prompt for additional input until valid input is received.
Pascal’s Triangle is a simple mathematical construct that begins with the value $ 1 $, and then each value below on the triangle is the sum of the two values immediately above it. The first few rows of Pascal’s Triangle are shown below:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1We can easily do this with loops and lists. So, let’s go through the process of building that program from scratch.
Handling Input
To begin, we can start with our usual program structure consisting of a main() function and a call to the main() function at the bottom of the file:
def main():
main()Next, we’ll include the positive_input() function that we’ve used in several previous labs, which handles prompting the user for a positive integer input and will prompt the user for additional input if an invalid value is provided. Once again, we’re doing our best to reuse pieces of code we’ve already written:
def positive_input():
x = int(input("Enter a positive integer: "))
while x <= 0:
print("Invalid input!")
x = int(input("Enter a positive integer: "))
return x
def main():
main()In our main() function, we can quickly call the positive_input() function to get the required piece of input from the user and store it in the variable n:
def positive_input():
x = int(input("Enter a positive integer: "))
while x <= 0:
print("Invalid input!")
x = int(input("Enter a positive integer: "))
return x
def main():
n = positive_input()
main()That’s the basic structure of our program to handle input. It’s very simple and mostly reused code, so it should be quick and easy to get to this point of our development process.
Initial Setup
Next, we should add some of the initial steps to our program. For example, we know that the first row of Pascal’s Triangle is simply the number $ 1 $, so we can create an initial list that contains just that single element, and then print that to the terminal:
def main():
n = positive_input()
row = [1]
print(row)Next, we know we need to create additional rows of Pascal’s Triangle, up to n rows in total. So, we can quickly build a for loop that will handle that in our main() function:
def main():
n = positive_input()
row = [1]
print(row)
for i in range(1, n):
# update row
print(row)Notice that we are starting our range at
$ 1 $ instead of
$ 0 $. This is because we’ve already printed the first row, so we only want to print additional rows if the value of n is greater than
$ 1 $. That’s the basic structure we need in our main() function
Computing the Next Row
Finally, we need to deal with the process of updating our row list to include the next row’s information. While we could do that directly in the main() function, it makes the most sense to create a separate method for that. So, we’ll start by creating a new function update_row() that requires a single parameter:
def update_row(row):In this function, we need to use the previous row on Pascal’s Triangle to compute the next row. This is a bit tricky to figure out, but thankfully there are a few helpful rules that we can follow:
- Each successive row is $ 1 $ element larger than the previous row
- The first item in the row is always $ 1 $
- The item at index
i+1of the new row is the sum of the items at indexiandi+1on the previous row. - The last item in the row is always $ 1 $
Using those rules, we can write a loop in code that will create a new list for the next row. First, since we’ll be using multiple items from the row list in our loop, we’ll need to start with the generic while loop structure to iterate through the list:
def update_row(row):
i = 0
while i < len(row):
# use list elements
i = i + 1We can also initialize our new list to start with the value $ 1 $ initially:
def update_row(row):
i = 0
new_row = [1]
while i < len(row):
# use list elements
i = i + 1Inside of the while loop, we can append new items to our new_row by simply summing the elements at index i and i + 1 of our previous list:
def update_row(row):
i = 0
new_row = [1]
while i < len(row):
new_row.append(row[i] + row[i + 1])
i = i + 1At the end, we’ll need to add the final $ 1 $ to the new row. Finally, since we’re creating a new list instead of modifying the existing one, we’ll need to return that reference back to the main function:
def update_row(row):
i = 0
new_row = [1]
while i < len(row):
new_row.append(row[i] + row[i + 1])
i = i + 1
new_row.append(1)
return new_rowIt may seem like we can simply do row = new_row in the update_row() method instead of returning it, but that actually doesn’t work. This is because the row variable in the update_row() function’s frame is a reference to the previous list in memory. If we update that reference, it will point to the new list in the update_row() function’s frame, but not in the main() frame - that variable still points to the previous list. You can confirm this behavior by testing it in Python Tutor to see how it looks in memory.
Final Program
The last step is to simply update the for loop in our main() function to call the update_row() function and store the returned list reference back into the row variable. So, our final program looks like this.
def positive_input():
x = int(input("Enter a positive integer: "))
while x <= 0:
print("Invalid input!")
x = int(input("Enter a positive integer: "))
return x
def update_row(row):
i = 0
new_row = [1]
while i < len(row):
new_row.append(row[i] + row[i + 1])
i = i + 1
new_row.append(1)
return new_row
def main():
n = positive_input()
row = [1]
print(row)
for i in range(1, n):
row = update_row(row)
print(row)
main()Now that we’ve completed this program, let’s test it once and make sure that it produces the correct output.
Logic Error
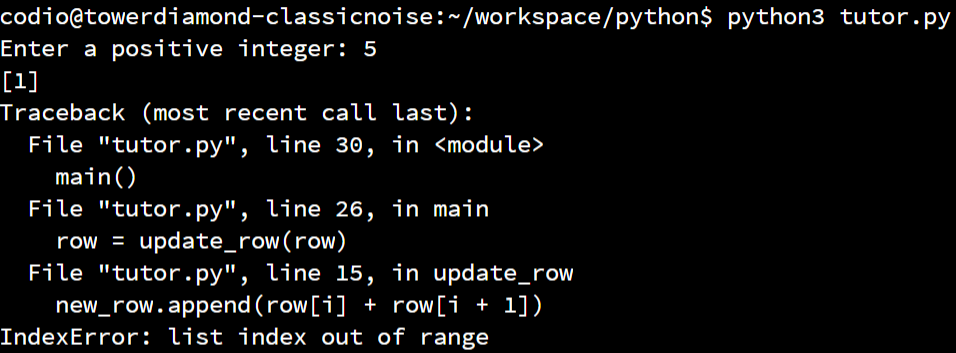
When we run this program, we should see the following appear in our terminal:
Uh oh! We’ve run into an error! This error is telling us that somewhere we are trying to access an index inside of a list that doesn’t exist. Helpfully, it tells us that we are doing this in the update_row() function, right inside of the for loop:
def update_row(row):
i = 0
new_row = [1]
while i < len(row):
new_row.append(row[i] + row[i + 1])
i = i + 1
new_row.append(1)
return new_rowSo, let’s see if we can figure out what is going on here. Let’s assume that it is failing when we are passing in the first row, which is simply the list [1]. On that line of code, we are appending a new item to the end of our new_list that is the sum of row[i] and row[i+1].
Ah ha! At this point, our row only contains a single item, so even if i is initially set to
$ 0 $, we cannot access an element that has index
$ 1 $ in that list. That’s where our logic error is coming from!
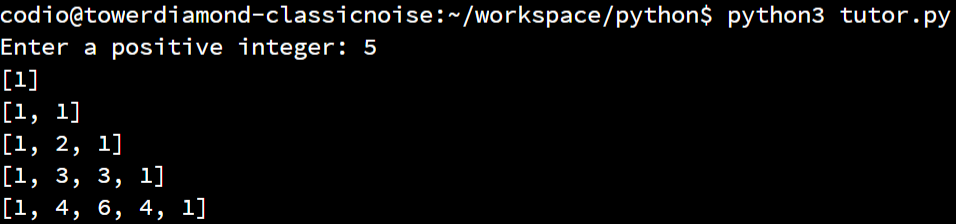
Since we need to access elements that are at one index higher than i, we must adjust our while loop so that it stops at the element before the last one. We can easily do that by modifying our while loop’s Boolean expression to i < len(row) - 1. If we make that change and try our program again, we should see the correct output:
The full, working example code is shown here:
def positive_input():
x = int(input("Enter a positive integer: "))
while x <= 0:
print("Invalid input!")
x = int(input("Enter a positive integer: "))
return x
def update_row(row):
i = 0
new_row = [1]
while i < len(row) - 1:
new_row.append(row[i] + row[i + 1])
i = i + 1
new_row.append(1)
return new_row
def main():
n = positive_input()
row = [1]
print(row)
for i in range(1, n):
row = update_row(row)
print(row)
main()There we go! We’ve written a complete program that will generate Pascal’s Triangle for any given number of rows. It uses both while and for loops and lists to accomplish that goal. Try to work through this entire example and run the program many times along the way to make sure you have a good understanding of why it works before continuing in this lab.
You might be wondering why we’ve chosen to keep the logic error in this example program instead of simply fixing it in our explanation. As it turns out, that logic error was actually made by the author while writing this example, and we felt that it was best to demonstrate how to quickly identify and resolve such an error instead of simply explaining it away. Hopefully seeing how easy it is to make simple logic errors like this will help you understand that it can happen to anyone, and it is not a big deal to have to fix small bugs along the way.