MyTree Recursive I

Again, we want to be able to implement a working version of a tree. From the last module, we had functions to add children, remove children, get attributes, and instantiate MyTree. We will now build upon that implementation to create a true tree.

Info

A recursive program is broken into two parts:

A base case—a simple version of the problem that can be solved directly, and
A recursive case—a general solution to the problem that uses smaller versions of the problem to compute the solution to the larger problem.

MyTree with recursion

Recall that in the previous module, we were not yet able to enforce the no cycle rule. We will now enforce this and add other tree functionality.

Info

Disclaimer: In the previous module we had a disclaimer that stated our implementation would not prevent cycles. The following functions and properties will implement recursion. Thus, we can maintain legal tree structures!

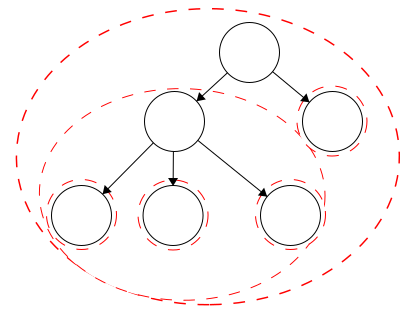
In the first module, we discussed how we can define trees recursively, meaning a tree consists of trees. We looked at the following example. Each red dashed line represented a distinct tree, thus we had five trees within the largest tree making six trees in total.

We will use our existing implementation from the first module. Now to make our tree recursive, we will include more getter functions as well as functions for traversals and defining node relationships.

Get depth, height, size, and root

We can define each of these recursively.

Get Depth

Depth - The depth of a node is its distance to the root. Thus, the root has depth zero.

We can define the depth of a node recursively:

Base case: we are at the root and the depth is zero
Recursive case: for any other node, the depth is 1 plus the depth of the parent

function GETDEPTH()
    if ROOT
        return 0
    else 
        return 1 + PARENT.GETDEPTH()
end function

Get Height

Height of a Node - The height of a node is the longest path to a leaf descendant. The height of a leaf is zero.

We can define the height of a node recursively:

Base case: we are at the leaf and the height is zero
Recursive case: for any other node, return 1 plus the maximum height of its children

function GETHEIGHT()
    if LEAF
        return 0
    else 
        MAX = 0
        for CHILD in CHILDREN
            CURR_HEIGHT = CHILD.GETHEIGHT()
            if CURR_HEIGHT > MAX
                MAX = CURR_HEIGHT
        return 1 + MAX
end function

Get Root

Root - the topmost node of the tree; a node with no parent.

We can define returning the root recursively:

Base case: we are at the root so return it
Recursive case: for any other node, return the root of the nodes parent

function GETROOT()
    if ISROOT()
        return this tree
    else
        return PARENT.GETROOT()
end function

Get Size

We define the size of a tree as the total number of children.

function GETSIZE()
    SIZE = 1
    for CHILD in CHILDREN
        SIZE += CHILD.GETSIZE()
    return SIZE
end function

Find a Value

To find a value within our tree, we will traverse down a branch as far as we can until we find the value. This will return the tree that has the value as the root.

function FIND(VALUE)
	if ITEM is VALUE
		return this node
	for CHILD in CHILDREN
		FOUND = CHILD.FIND(VALUE)
		if FOUND is not NONE
			return FOUND
	return NONE
end function