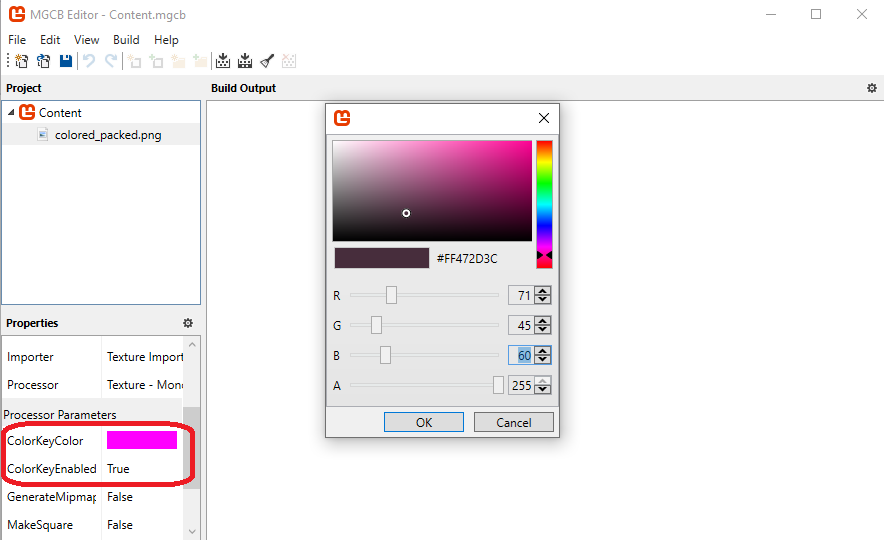
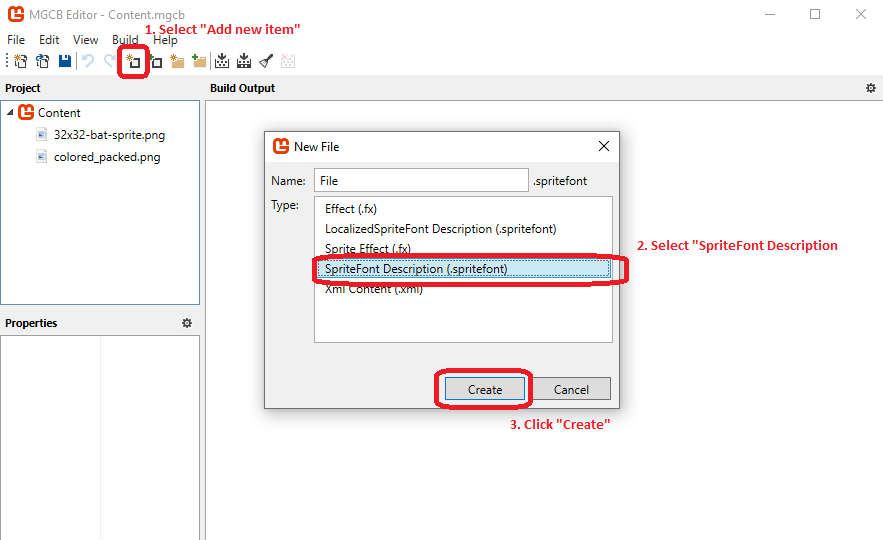
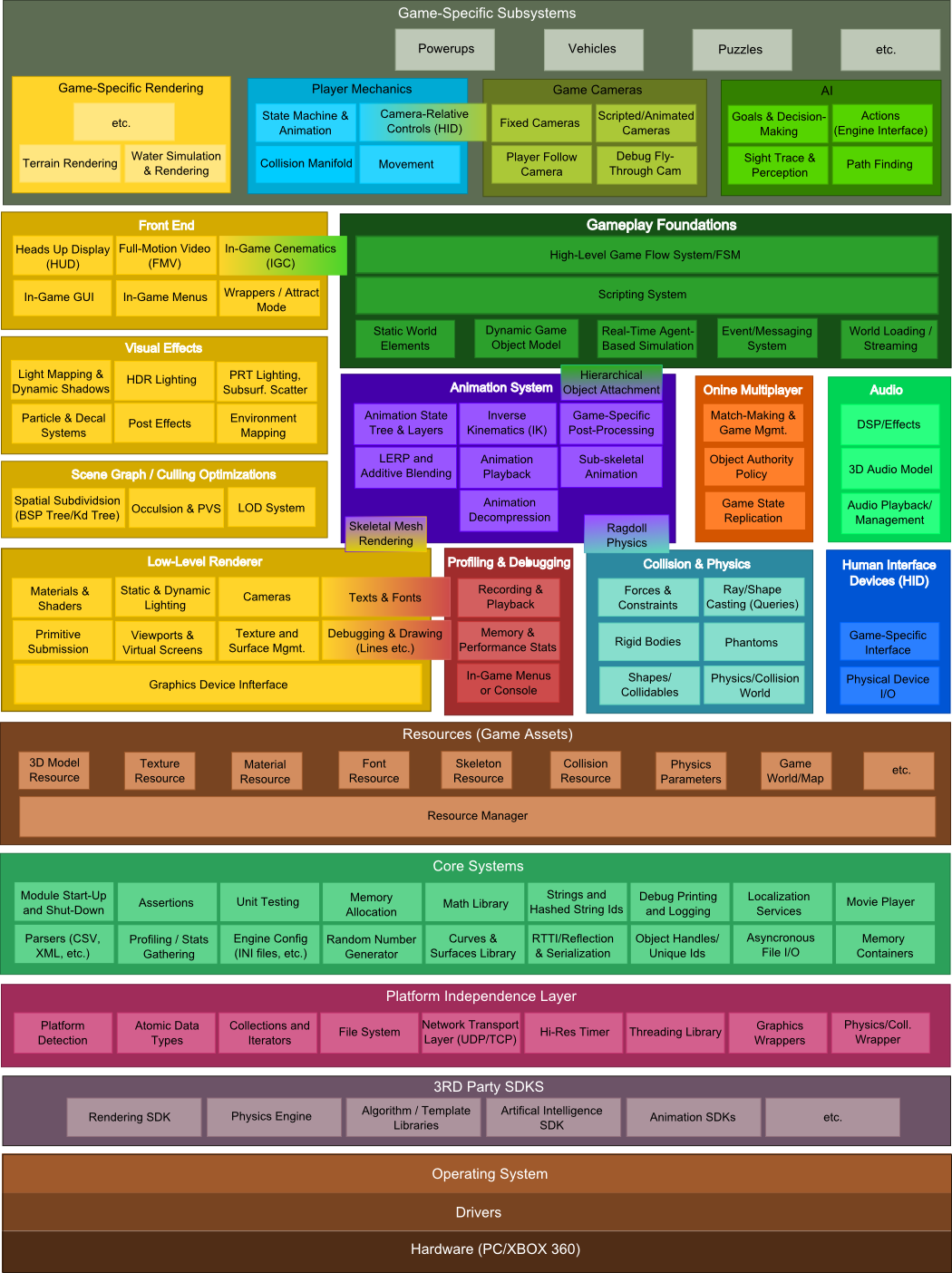
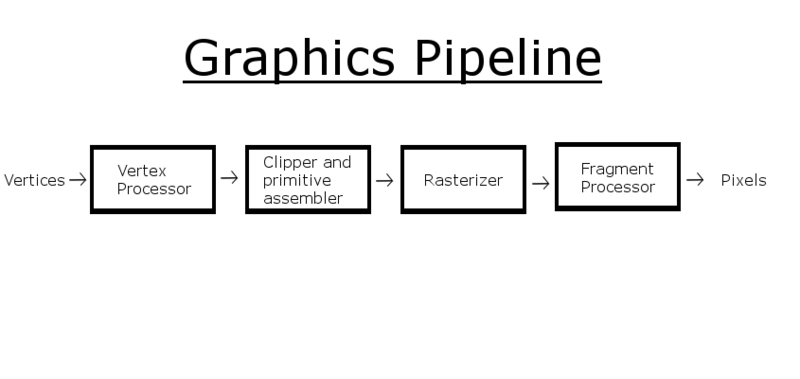
Course Structure
Web Only
This textbook was authored for the CIS 580 - Fundamentals of Game Programming course at Kansas State University. This front matter is specific to that course. If you are not enrolled in the course, please disregard this section.
A good portion of this course is devoted to learning about algorithms, data structures, and design patterns commonly used in constructing computer games. To introduce and learn about each of these topics we have adopted the following pedagogical strategies:
- To introduce the topic, you will read a textbook chapter or watch a recorded lecture on the theory behind the algorithm, data structure, or design pattern.
- You will then be asked to follow video tutorial to implement the approach in a sample/demo project. When you finish, you will submit the project you have created.
- You will then be challenged to use the approach in one (or more) original game assignments. This requires some thought of what kind of game makes sense for the approach, and it needs to be adapted to work with that game.
In addition to learning about the programming techniques used in games, you are also challenged to build good games. This requires you to consider games from the standpoint of an aesthetic experience, much like any form of art or literature. Accordingly, we are borrowing some techniques from the study of creative subjects:
- Some of your readings will be focused on the aesthetics of game design. Why do we play games? What makes a good game?
- For each original game you produce, a portion of the grade will be derived from the aesthetic experience it provides, i.e. is it fun? Does it invoke emotional responses from the player?
- You will also engage in activities focused on critiquing games - evaluating them in terms of an aesthetic experience. What works in the game design? What helps you engage as a player? What doesn’t work in the game design? What interferes with your ability to enjoy the game?
- You will also submit some of your original games to be “workshopped” by the class - critiqued by your peers as a strategy to help you evaluate your own work.
Class Meetings
This class is presented in a “flipped” format. This means that you will need to do readings and work through tutorials before the class period. Instead of lectures, class meetings are reserved for discussion, brainstorming, development, and workshops. Attendance is expected - remember class time is your opportunity to ask questions, get help, and garner feedback on your game designs. Active participation in discussions and critiques is likewise expected.
Info
In the case of illness, you should not attend class in-person, but may join via Zoom by notifying me before class begins. This will allow you to participate to the best of your ability. However, this option should only be used for illness.
Course Modules
The course activities have been organized into modules in Canvas which help group related materials and activities. You should work your way through each module from start to finish.
Course Readings
Most modules will contain assigned readings and/or videos for you to study as a first step towards understanding the topic. These are drawn from a variety of sources, and are all available on Canvas.
We will make heavy use of Robert Nystrom’s Game Programming Patterns, an exploration of common design patterns used in video games. It can be bought in print, but he also has a free web version: https://gameprogrammingpatterns.com/contents.html.
Course Tutorials
Most modules will also contain a tutorial exploring implementing the covered topic with the MonoGame/XNA technologies we will be using in this course. These are organized into the course textbook (which you are reading now). It is available in its entirety at https://textbooks.cs.ksu.edu/cis580/.
Original Game Assignments
Every few topics you will be challenged to create an original game that draws upon the techniques you have learned about. For each game, there will be a limited number of algorithms, data structures, or approaches you are required to implement. Each original game is worth 100 points.
These are graded using criterion grading, an approach where your assignment is evaluated according to a set criteria. If it meets the criteria, you get full points. If it doesn’t, you get 0 points. The criteria for your games are twofold. First, you must implement the required techniques within your game. If you do, you earn 70 points. If you don’t, you earn 0. For games that meet the criteria, they are further evaluated as a game. If you have created a playable game that is at least somewhat fun and aesthetically pleasing, you can earn an additional 30 points.
I have adopted this grading system as I have found it allows for more creative freedom for students in creating their games than a detailed rubric does (which, by its very nature forces you to make a particular kind of game). However, I do recognize that some students struggle with the lack of a clear end goal. If this is the case for you, I suggest you speak with myself, the TAs, or the class to brainstorm ideas of what kind of game you can build to achieve the criteria.
Serial Submissions
In this course, it is acceptable to submit the same game project for multiple assignments. Each time you submit your game, you will need to incorporate the new set of requirements. This allows you to make more complex games by evolving a concept through multiple iterations.
Working in Teams
You may work with other students as a team to develop no more than three of your original game submissions. These cannot be one of the first four original game assignments. If you choose to work as a team, you must send me a message in Ed Discussion board listing each member of the team, ideally before you start working on the game. Students working on teams will also be required to submit a peer review evaluating the contributions of each member of the team. This will be used to modify the game score assigned to each student. Be aware that I will not tolerate students letting their teammates do all the work - any student who does will receive a 0 for the assignment.
Workshopping is an approach common to the creative arts that we are adapting to game design. Each student will have the opportunity to workshop their games during the semester. In addition, for your first two workshops you may and earn up to 100 extra credit points (50 points for each).
Workshops will be held on Wednesdays, and we can have up to four workshops per day. Workshops are available on a first-come basis. To reserve your slot, You must sign up by posting to the Workshops discussion board in Canvas.
The class should play the week’s workshop games before the class meeting on Wednesday. In that class meeting we will discuss the game for ~10 minutes while the creator of the game remains a silent observer and takes notes. After this time has elapsed, the team can ask questions of the game creator, and visa versa. During these workshops, please use good workshop etiquette.
Warning
In order to earn points for a workshop, you must:
- Post your game to be workshopped before the Monday of the week the workshop will be held.
- This post should include a description of your game, and a link to a release in your public GitHub repository for the game.
- The release must contain the game binaries as additional downloads, i.e. zip your release build folder and upload it to the GitHub release page.
If one or more of these conditions are not met, you will earn NO POINTS for your workshop.
Where to Find Help
Web Only
This textbook was authored for the CIS 580 - Fundamentals of Game Programming course at Kansas State University. This front matter is specific to that course. If you are not enrolled in the course, please disregard this section.
As you work on the materials in this course, you may run into questions or problems and need assistance.
Class Sessions
A portion of each class session is set aside for questions that have come up as you’ve worked through the course materials. Please take advantage of this time; not only will you benefit from the answer, but so will your classmates!
Ed Discussions Forum
For questions that crop up outside of class times, your first line of communication for this course is the Ed Discussions forum, which can be reached through Canvas. This forum allows you to post questions which can be answered by me or your classmates, which can be searched by everyone in the class. In addition, it allows for anonymous postings (if you feel uncomfortable letting people know who is asking), or write posts that can only be viewed by the instructor (for questions about grades, etc). The Ed Discussions forum also has good support for writing posts in markdown and writing an displaying code snippets.
Info
The helping hand extra credit assignment provides bonus points for students who are caught helping other students in the class Ed Discussions.
Other Features
Ed Discussions includes lots of useful features:
- Use the
@ symbol with a username in a message to create a mention, which notifies that user immediately, i.e. @Nathan Bean will alert me that you’ve made a post that mentions me.
- Use the backtick mark (, i.e.
`var c = 4;`) to enclose code snippets to format them as programming code, and triple backtick marks to enclose multiple lines of code (```[multiline code]```).
- You can also set your status to indicate your current availability.
Email
Ed Discussions is the preferred communication medium for the course because 1) you will generally get a faster response than email, and 2) writing code in email is a terrible experience, both to write and to read. Ed Discussions’s support of markdown syntax makes including code comments much easier on both of us.
However, if you have issues with Ed Discussions, feel free to email one of the instructors directly if you are unable to post directly on Ed Discussions itself for some reason.
Game Development Club
Another great resource available to you is the Kansas State University Game Development Club. You can learn more at the club website https://gdc.cs.ksu.edu/. They also have a channel on the departmental Discord Server, #game-dev-club.
Other Avenues for Help
There are a few resources available to you that you should be aware of. First, if you have any issues working with K-State Canvas, K-State IT resources, or any other technology related to the delivery of the course, your first source of help is the K-State IT Helpdesk. They can easily be reached via email at helpdesk@ksu.edu. Beyond them, there are many online resources for using Canvas, all of which are linked in the resources section below the video. As a last resort, you may also want to post in Discord, but in most cases we may simply redirect you to the K-State helpdesk for assistance.
If you have issues with the technical content of the course, specifically related to completing the tutorials and projects, there are several resources available to you. First and foremost, make sure you consult the vast amount of material available in the course modules, including the links to resources. Usually, most answers you need can be found there.
If you are still stuck or unsure of where to go, the next best thing is to post your question on Discord, or review existing discussions for a possible answer. You can find the link to the left of this video. As discussed earlier, the instructors, TAs, and fellow students can all help answer your question quickly.
Of course, as another step you can always exercise your information-gathering skills and use online search tools such as Google to answer your question. While you are not allowed to search online for direct solutions to assignments or projects, you are more than welcome to use Google to access programming resources such as The MonoGame Documentation, the Microsoft Developer Network, C# language documentation, and other tutorials. I can definitely assure you that programmers working in industry are often using Google and other online resources to solve problems, so there is no reason why you shouldn’t start building that skill now.
Next, we have grading and administrative issues. This could include problems or mistakes in the grade you received on a project, missing course resources, or any concerns you have regarding the course and the conduct of myself and your peers. You’ll be interacting with us on a variety of online platforms and sometimes things happen that are inappropriate or offensive. There are lots of resources at K-State to help you with those situations. First and foremost, please DM me on Ed Discussions as soon as possible and let me know about your concern, if it is appropriate for me to be involved. If not, or if you’d rather talk with someone other than me about your issue, I encourage you to contact either your academic advisor, the CS department staff, College of Engineering Student Services, or the K-State Office of Student Life. Finally, if you have any concerns that you feel should be reported to K-State, you can do so at https://www.k-state.edu/report/. That site also has links to a large number of resources at K-State that you can use when you need help.
Finally, if you find any errors or omissions in the course content, or have suggestions for additional resources to include in the course, DM the instructors on Discord. There are some extra credit points available for helping to improve the course, so be on the lookout for anything that you feel could be changed or improved.
Info
The Bug Bounty extra credit assignment gives points for finding errors in the course materials. Remember, your instructors are human, and do make mistakes! But we don’t want those occasional mistakes to trip you and your peers up in your learning efforts, so bringing them to our attention is appreciated.
So, in summary, Ed Discussions should always be your first stop when you have a question or run into a problem. For issues with Canvas or Visual Studio, you are also welcome to refer directly to the resources for those platforms. For questions specifically related to the projects, use Ed Discussions for sure. For grading questions and errors in the course content or any other issues, please DM the instructors on Ed Discussions for assistance.
Our goal in this program is to make sure that you have the resources available to you to be successful. Please don’t be afraid to take advantage of them and ask questions whenever you want.
Resources
Syllabus
Web Only
This textbook was authored for the CIS 580 - Fundamentals of Game Programming course at Kansas State University. This front matter is specific to that course. If you are not enrolled in the course, please disregard this section.
CIS 580 - Fundamentals of Game Programming
Previous Versions
- Instructor: Nathan Bean (nhbean AT ksu DOT edu)
- Office: DUE 2216
- Phone: (785)483-9264 (Call/Text)
- Website: https://nathanhbean.com
- Office Hours: WU 1:00-2:00 or by appointment
Preferred Methods of Communication:
- Chat: Quick questions via Ed Discussions are the preferred means of communication. Questions whose answers may benefit the class I would encourage you to post publicly. More personal questions should be direct messaged to
@Nathan Bean.
- Email: For questions outside of this course, email to nhbean@ksu.edu is preferred.
- Phone/Text: 785-483-9264 Emergencies only! I will do my best to respond as quickly as I can.
Prerequisites
- CIS 501
- MATH 221
- A physics course
Students may enroll in CIS courses only if they have earned a grade of C or better for each prerequisite to these courses.
Course Overview
Fundamental principles of programming games. Foundational game algorithms and data structures. Two-dimensional graphics and game world simulation. Development for multiple platforms. Utilization of game programming libraries. Design of multiple games incorporating topics covered.
Course Description
This course is intended to introduce the fundamentals of creating computer game systems. Computer
games are uniquely challenging in the field of software development, as they are considerably complex
systems composed of many interconnected subsystems that draw upon the breadth of the field - and
must operate within real-time constraints. For this semester, my goals for you as a student are:
- To develop a broad understanding of the algorithms and data structures often utilized within
games.
- To recognize that there are many valid software designs, and to learn to evaluate them in terms
of their appropriateness and trade-offs.
- To expand your games portfolio with fun, engaging, and technically sophisticated games of your
own devising.
- To practice the software development and communication skills needed to participate
meaningfully within our industry.
All of our activities this semester will be informed by these goals.
Major Course Topics
- Game Loops
- Input
- Sprite Rendering and Animation
- Collision Detection and Restitution
- Physics Simulation
- Parallax Scrolling
- Tile Engines
- Game State Management
- Content Management
- 3D Rendering Fundamentals
- Rendering and Animating Models
Course Structure
A common axiom in learner-centered teaching is “(s)he who does the work does the learning.” What this really means is that students primarily learn through grappling with the concepts and skills of a course while attempting to apply them. Simply seeing a demonstration or hearing a lecture by itself doesn’t do much in terms of learning. This is not to say that they don’t serve an important role - as they set the stage for the learning to come, helping you to recognize the core ideas to focus on as you work. The work itself consists of applying ideas,
practicing skills, and putting the concepts into your own words.
This course is built around learner-centered teaching and its recognition of the role and
importance of these different aspects of learning. Most modules will consist of readings interspersed with a variety of hands-on activities built around the concepts and skills we are seeking to master. In addition, we will be applying these ideas in iteratively building a series of original video games over the semester. Part of our class time will be reserved for working on and discussing these games, giving you the chance to ask questions and receive feedback from your instructors, UTAs, and classmates.
The Work
There is no shortcut to becoming a great game programmer. Only by doing the work will you develop the skills and knowledge to make your a successful game developer. This course is built around that principle, and gives you ample opportunity to do the work, with as much support as we can offer.
Readings
Each module will include assigned readings focusing on both game programming theory and concrete approaches using MonoGame. You will need to read these to establish the theoretical and practical foundations for tackling the tutorials and original game projects.
Tutorials
Each module will include tutorial assignments that will take you step-by-step through using a particular concept or technique. The point is not simply to complete the tutorial, but to practice the technique and coding involved. You will be expected to implement these techniques on your own in your game projects - so this practice helps prepare you for those assignments.
Original Game Programming Assignments
Throughout the semester you will be building original games incorporating the techniques you have been learning; every two weeks a new game build will be due. These games can be completely new games, or build on games you turned in as a prior project, incorporating the new assigned techniques.
These original game projects are graded using criterion grading, and approach that only assigns points for completing the full requirements. However, the requirements will be brief and straightforward, i.e.:
Create a game that detects collisions between sprites and responds by altering the simulation in a significant way (i.e. changing sprite direction, removing sprites from the game, increasing or decreasing health, etc).
Games that meet the assigned criteria will be awarded 70 points.
In addition, games that fulfill aesthetic goals of being engaging and/or eliciting emotions from the player (other than frustration) will be awarded an additional 30 points. This is largely focused on what separates a game from a technical demo. Your game doesn’t have to be world-shattering to earn these points, just playable and somewhat fun.
You have the option of collaborating with other students in the class to create larger, group games for any original game project after the first four. As part of participating in a group development effort, you must complete a peer review for each of your teammates, due along with the game. The results of the peer review will be shared with your teammates to help develop teamwork skills. Additionally, your individual grade for the game assignment may be modified based on the peer review feedback.
Workshops
Over the course of the semester, you will have the opportunity to have your games be workshopped by your peers. This is a valuable opportunity to gain critical feedback on your work, and you can earn up to 100 extra credit points (the equivalent of one game assignment) for each game you workshop.
Each week you should download and play the games that will be workshopped that week and be ready to discuss the game in class.
Exams
There will be no exams given in this course.
Grading
In theory, each student begins the course with an A. As you submit work, you can either maintain your A (for good work) or chip away at it (for less adequate or incomplete work). In practice, each student starts with 0 points in the gradebook and works upward toward a final point total out of the possible number of points. In this course, it is perfectly possible to get an A simply by completing all the software milestones in a satisfactory manner and attending and participating in class each day. In such a case, the examinations will simply reflect the learning you’ve been doing through that work. Each work category constitutes a portion of the final grade, as detailed below:
38% - Activities (The lowest score is dropped)
42% - Original Game Projects (7% each, 7 games total)
20% - Final Game
Extra Credit
14% - Workshops (7% each, 2 workshops total)
Letter grades will be assigned following the standard scale:
90% - 100% - A; 80% - 89.99% - B; 70% - 79.99% - C; 60% - 69.99% - D; 00% - 59.99% - F
Collaboration
Collaboration is an important practice for both learning and software development. As such, you are encouraged to work with peers and seek out help from your instructors and UTAs. However, it is also critical to remember that (s)he who does the work, does the learning. Relying too much on your peers will deny you the opportunity to learn yourself.
Game development is almost always a team activity, so you may choose to tackle the later game projects in a team. Obviously, a high degree of collaboration is expected here. Be aware that this does not mean you have the opportunity to let your team do all the work. Students who have not contributed (based on their peer reviews) will receive a 0 on team game projects.
Late Work
Warning
Read the late work policy very carefully! If you are unsure how to interpret it, please contact the instructor via email. Not understanding the policy does not mean that it won’t apply to you!
Every student should strive to turn in work on time. Late work will receive a penalty of 10% of the possible points for each day it is late. If you are getting behind in the class, you are encouraged to speak to the instructor for options to make up missed work.
Software
We will be using Visual Studio 2022 as our development environment. You can download a free copy of Visual Studio Community for your own machine at
https://visualstudio.microsoft.com/downloads/. You should also be able to get a professional
development license through your Azure Student Portal. See the CS support documentation for details: https://support.cs.ksu.edu/CISDocs/wiki/FAQ#MSDNAA
MonoGame is available through the Nuget package manager built into Visual Studio. You can install MonoGame project templates by following the directions here: https://docs.monogame.net/articles/getting_started/2_choosing_your_ide_visual_studio.html#install-monogame-extension-for-visual-studio-2022l.
Recommended Texts & Supplies
To participate in this course, students must have access to a modern web browser, broadband internet connection, and webcam and microphone. All course materials will be provided via Canvas. Modules may also contain links to external resources for additional information, such as programming language documentation.
This course offers an instructor-written textbook, which is broken up into a specific reading order and interleaved with activities and quizzes in the modules. It can also be directly accessed at https://textbooks.cs.ksu.edu/cis580/.
Additionally, we will be using Robert Nystrom’s Game Programming Patterns, an exploration of common design patterns used in video games. It can be bought in print, but he also has a free web version at https://gameprogrammingpatterns.com/contents.html
Students who would like additional textbooks should refer to resources available on the O’Riley For Higher Education digital library offered by the Kansas State University Library. These include electronic editions of popular textbooks as well as videos and tutorials.
Subject to Change
The details in this syllabus are not set in stone. Due to the flexible nature of this class, adjustments may need to be made as the semester progresses, though they will be kept to a minimum. If any changes occur, the changes will be posted on the Canvas page for this course and emailed to all students.
K-State 8
CIS 580 helps satisfy the Aesthetic Interpretation tag in the K-State 8 General Education program. As part of this course, you will both develop and critique computer games, which constitute a form of aesthetic expression that is both similar and dissimilar from literature and film.
Academic Honesty
Kansas State University has an Honor and Integrity System based on personal integrity, which is presumed to be sufficient assurance that, in academic matters, one’s work is performed honestly and without unauthorized assistance. Undergraduate and graduate students, by registration, acknowledge the jurisdiction of the Honor and Integrity System. The policies and procedures of the Honor and Integrity System apply to all full and part-time students enrolled in undergraduate and graduate courses on-campus, off-campus, and via distance learning. A component vital to the Honor and Integrity System is the inclusion of the Honor Pledge which applies to all assignments, examinations, or other course work undertaken by students. The Honor Pledge is implied, whether or not it is stated: “On my honor, as a student, I have neither given nor received unauthorized aid on this academic work.” A grade of XF can result from a breach of academic honesty. The F indicates failure in the course; the X indicates the reason is an Honor Pledge violation.
For this course, a violation of the Honor Pledge will result in an automatic 0 for the assignment and the violation will be reported to the Honor System. A second violation will result in an XF in the course.
In this course, unauthorized aid broadly consists of giving or receiving code to complete assignments. This could be code you share with a classmate, code you have asked a third party to write for you, or code you have found online or elsewhere.
Authorized aid - which is not a violation of the honor policy - includes using the code snippets provided in the course materials, discussing strategies and techniques with classmates, instructors, TAs, and mentors. Additionally, you may use code snippets and algorithms found in textbooks and web sources if you clearly label them with comments indicating where the code came from and how it is being used in your project.
Be aware that using assets (images, sounds, etc.) that you do not have permission to use constitutes both unauthorized aid and copyright infringement.
Standard Syllabus Statements
Info
The statements below are standard syllabus statements from K-State and our program. The latest versions are available online here.
Students with Disabilities
At K-State it is important that every student has access to course content and the means to demonstrate course mastery. Students with disabilities may benefit from services including accommodations provided by the Student Access Center. Disabilities can include physical, learning, executive functions, and mental health. You may register at the Student Access Center or to learn more contact:
- Manhattan/Olathe/Global Campus – Student Access Center
- K-State Salina Campus – Julie Rowe; Student Success Coordinator
Students already registered with the Student Access Center please request your Letters of Accommodation early in the semester to provide adequate time to arrange your approved academic accommodations. Once SAC approves your Letter of Accommodation it will be e-mailed to you, and your instructor(s) for this course. Please follow up with your instructor to discuss how best to implement the approved accommodations.
Expectations for Conduct
All student activities in the University, including this course, are governed by the Student Judicial Conduct Code as outlined in the Student Governing Association By Laws, Article V, Section 3, number 2. Students who engage in behavior that disrupts the learning environment may be asked to leave the class.
Mutual Respect and Inclusion in K-State Teaching & Learning Spaces
At K-State, faculty and staff are committed to creating and maintaining an inclusive and supportive learning environment for students from diverse backgrounds and perspectives. K-State courses, labs, and other virtual and physical learning spaces promote equitable opportunity to learn, participate, contribute, and succeed, regardless of age, race, color, ethnicity, nationality, genetic information, ancestry, disability, socioeconomic status, military or veteran status, immigration status, Indigenous identity, gender identity, gender expression, sexuality, religion, culture, as well as other social identities.
Faculty and staff are committed to promoting equity and believe the success of an inclusive learning environment relies on the participation, support, and understanding of all students. Students are encouraged to share their views and lived experiences as they relate to the course or their course experience, while recognizing they are doing so in a learning environment in which all are expected to engage with respect to honor the rights, safety, and dignity of others in keeping with the K-State Principles of Community.
If you feel uncomfortable because of comments or behavior encountered in this class, you may bring it to the attention of your instructor, advisors, and/or mentors. If you have questions about how to proceed with a confidential process to resolve concerns, please contact the Student Ombudsperson Office. Violations of the student code of conduct can be reported using the Code of Conduct Reporting Form. You can also report discrimination, harassment or sexual harassment, if needed.
Netiquette
Info
This is our personal policy and not a required syllabus statement from K-State. It has been adapted from this statement from K-State Online, and theRecurse Center Manual. We have adapted their ideas to fit this course.
Online communication is inherently different than in-person communication. When speaking in person, many times we can take advantage of the context and body language of the person speaking to better understand what the speaker means, not just what is said. This information is not present when communicating online, so we must be much more careful about what we say and how we say it in order to get our meaning across.
Here are a few general rules to help us all communicate online in this course, especially while using tools such as Canvas or Discord:
- Use a clear and meaningful subject line to announce your topic. Subject lines such as “Question” or “Problem” are not helpful. Subjects such as “Logic Question in Project 5, Part 1 in Java” or “Unexpected Exception when Opening Text File in Python” give plenty of information about your topic.
- Use only one topic per message. If you have multiple topics, post multiple messages so each one can be discussed independently.
- Be thorough, concise, and to the point. Ideally, each message should be a page or less.
- Include exact error messages, code snippets, or screenshots, as well as any previous steps taken to fix the problem. It is much easier to solve a problem when the exact error message or screenshot is provided. If we know what you’ve tried so far, we can get to the root cause of the issue more quickly.
- Consider carefully what you write before you post it. Once a message is posted, it becomes part of the permanent record of the course and can easily be found by others.
- If you are lost, don’t know an answer, or don’t understand something, speak up! Email and Canvas both allow you to send a message privately to the instructors, so other students won’t see that you asked a question. Don’t be afraid to ask questions anytime, as you can choose to do so without any fear of being identified by your fellow students.
- Class discussions are confidential. Do not share information from the course with anyone outside of the course without explicit permission.
- Do not quote entire message chains; only include the relevant parts. When replying to a previous message, only quote the relevant lines in your response.
- Do not use all caps. It makes it look like you are shouting. Use appropriate text markup (bold, italics, etc.) to highlight a point if needed.
- No feigning surprise. If someone asks a question, saying things like “I can’t believe you don’t know that!” are not helpful, and only serve to make that person feel bad.
- No “well-actually’s.” If someone makes a statement that is not entirely correct, resist the urge to offer a “well, actually…” correction, especially if it is not relevant to the discussion. If you can help solve their problem, feel free to provide correct information, but don’t post a correction just for the sake of being correct.
- Do not correct someone’s grammar or spelling. Again, it is not helpful, and only serves to make that person feel bad. If there is a genuine mistake that may affect the meaning of the post, please contact the person privately or let the instructors know privately so it can be resolved.
- Avoid subtle -isms and microaggressions. Avoid comments that could make others feel uncomfortable based on their personal identity. See the syllabus section on Diversity and Inclusion above for more information on this topic. If a comment makes you uncomfortable, please contact the instructor.
- Avoid sarcasm, flaming, advertisements, lingo, trolling, doxxing, and other bad online habits. They have no place in an academic environment. Tasteful humor is fine, but sarcasm can be misunderstood.
As a participant in course discussions, you should also strive to honor the diversity of your classmates by adhering to the K-State Principles of Community.
Discrimination, Harassment, and Sexual Harassment
Kansas State University is committed to maintaining academic, housing, and work environments that are free of discrimination, harassment, and sexual harassment. Instructors support the University’s commitment by creating a safe learning environment during this course, free of conduct that would interfere with your academic opportunities. Instructors also have a duty to report any behavior they become aware of that potentially violates the University’s policy prohibiting discrimination, harassment, and sexual harassment, as outlined by PPM 3010.
If a student is subjected to discrimination, harassment, or sexual harassment, they are encouraged to make a non-confidential report to the University’s Office of Civil Rights and Title IX (OCR & TIX) using the online reporting form. Incident disclosure is not required to receive resources at K-State. Reports that include domestic and dating violence, sexual assault, or stalking, should be considered for reporting by the complainant to the Kansas State University Police Department or the Riley County Police Department. Reports made to law enforcement are separate from reports made to OIE. A complainant can choose to report to one or both entities. Confidential support and advocacy can be found with the K-State Center for Advocacy, Response, and Education (CARE). Confidential mental health services can be found with Lafene Counseling and Psychological Services (CAPS). Academic support can be found with the Student Support and Accountability (SSA) office. SSA is a non-confidential resource. OCR & TIX also provides a comprehensive list of resources on their website. If you have questions about non-confidential and confidential resources, please contact OCR & TIX at civilrights@k-state.edu or (785) 532–6220.
Academic Freedom Statement
Kansas State University is a community of students, faculty, and staff who work together to discover new knowledge, create new ideas, and share the results of their scholarly inquiry with the wider public. Although new ideas or research results may be controversial or challenge established views, the health and growth of any society requires frank intellectual exchange. Academic freedom protects this type of free exchange and is thus essential to any university’s mission.
Moreover, academic freedom supports collaborative work in the pursuit of truth and the dissemination of knowledge in an environment of inquiry, respectful debate, and professionalism. Academic freedom is not limited to the classroom or to scientific and scholarly research, but extends to the life of the university as well as to larger social and political questions. It is the right and responsibility of the university community to engage with such issues.
Campus Safety
Kansas State University is committed to providing a safe teaching and learning environment for student and faculty members. In order to enhance your safety in the unlikely case of a campus emergency make sure that you know where and how to quickly exit your classroom and how to follow any emergency directives. Current Campus Emergency Information is available at the University’s Advisory webpage.
Student Resources
K-State has many resources to help contribute to student success. These resources include accommodations for academics, paying for college, student life, health and safety, and others. Check out the Student Guide to Help and Resources: One Stop Shop for more information.
Student Academic Creations
Student academic creations are subject to Kansas State University and Kansas Board of Regents Intellectual Property Policies. For courses in which students will be creating intellectual property, the K-State policy can be found at University Handbook, Appendix R: Intellectual Property Policy and Institutional Procedures (part I.E.). These policies address ownership and use of student academic creations.
Mental Health
Your mental health and good relationships are vital to your overall well-being. Symptoms of mental health issues may include excessive sadness or worry, thoughts of death or self-harm, inability to concentrate, lack of motivation, or substance abuse. Although problems can occur anytime for anyone, you should pay extra attention to your mental health if you are feeling academic or financial stress, discrimination, or have experienced a traumatic event, such as loss of a friend or family member, sexual assault or other physical or emotional abuse.
If you are struggling with these issues, do not wait to seek assistance.
For Kansas State Salina Campus:
For Global Campus/K-State Online:
University Excused Absences
K-State has a University Excused Absence policy (Section F62). Class absence(s) will be handled between the instructor and the student unless there are other university offices involved. For university excused absences, instructors shall provide the student the opportunity to make up missed assignments, activities, and/or attendance specific points that contribute to the course grade, unless they decide to excuse those missed assignments from the student’s course grade. Please see the policy for a complete list of university excused absences and how to obtain one. Students are encouraged to contact their instructor regarding their absences.
Copyright Notice
©2025 The materials in this online course fall under the protection of all intellectual property, copyright and trademark laws of the U.S. The digital materials included here come with the legal permissions and releases of the copyright holders. These course materials should be used for educational purposes only; the contents should not be distributed electronically or otherwise beyond the confines of this online course. The URLs listed here do not suggest endorsement of either the site owners or the contents found at the sites. Likewise, mentioned brands (products and services) do not suggest endorsement. Students own copyright to what they create.
Original content in the course textbook at https://textbooks.cs.ksu.edu/cis580/ is licensed under a Creative Commons BY-SA license by Nathan Bean unless otherwise stated.