Branching Constructs
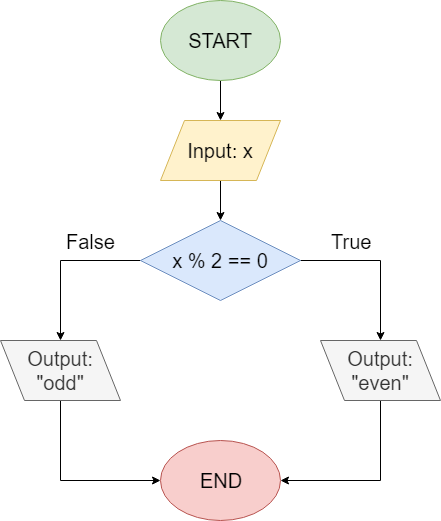
Let’s take a look at a second flowchart. For this program, we’ll have the user input a number. If the number is even, we’ll output even, but if it is odd, we’ll output odd. Let’s look at what this program might look like as a flowchart:
This flowchart uses a diamond-shaped block to indicate a decision we’d like our computer program to make. Inside the block, we see the Boolean logic expression x % 2 == 0, which will determine whether x is evenly divisible by
$ 2 $. If so, the result of the modulo operation would be
$ 0 $, so the entire statement would evaluate to true, indicating that x is an even number.
We also see two arrows coming from this block, one on the left if the statement is false, and another, on the right, if the statement is true. Each path leads to a different output, before being joined together at the end.
Nearly every programming language supports a method for running different parts of code based on the result of some Boolean logic expression, just like in this example. Collectively, these methods are known as conditional constructs, sometimes referred to as conditional statements or just conditionals. In the example above, the diamond-shaped block represents a conditional construct in that program.
Complex Decisions
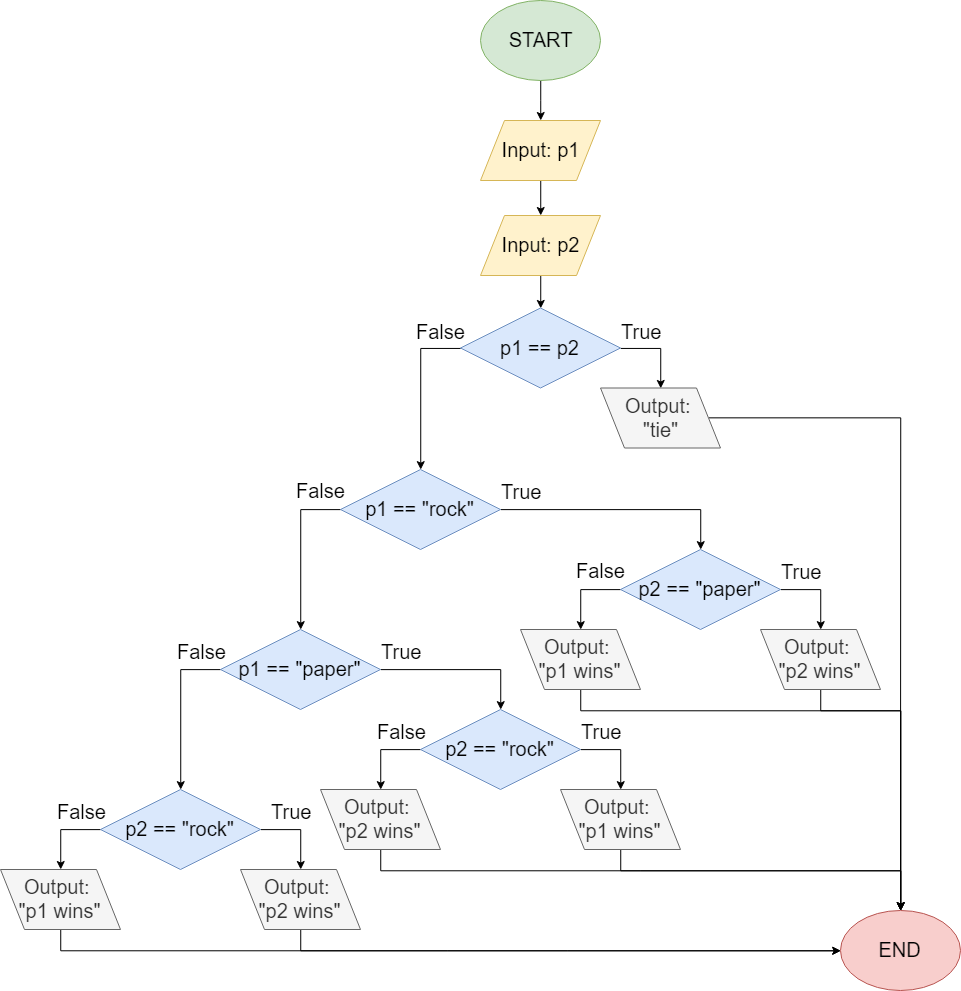
Of course, we can make even more complicated decisions in our programs. Let’s take a look at one more flowchart and see if we can understand what this program does:
At first glance, this flowchart may seem quite confusing. However, by looking closely at the decisions it makes and the corresponding output, we should realize that it is a program that plays the common “Rock, Paper, Scissors” game.
First, the program accepts two inputs, representing the symbols chosen by each player, and stores them in variables p1 and p2. Then, it checks to see if the inputs are equal. If so, the program declares the game to be a tie by outputting tie, and then it ends. If the inputs are not equal, then it can determine a winner.
Instead of trying to describe how the rest of the program works, let’s look at a few possible inputs and trace the program’s execution through the flowchart, just to see what it does.
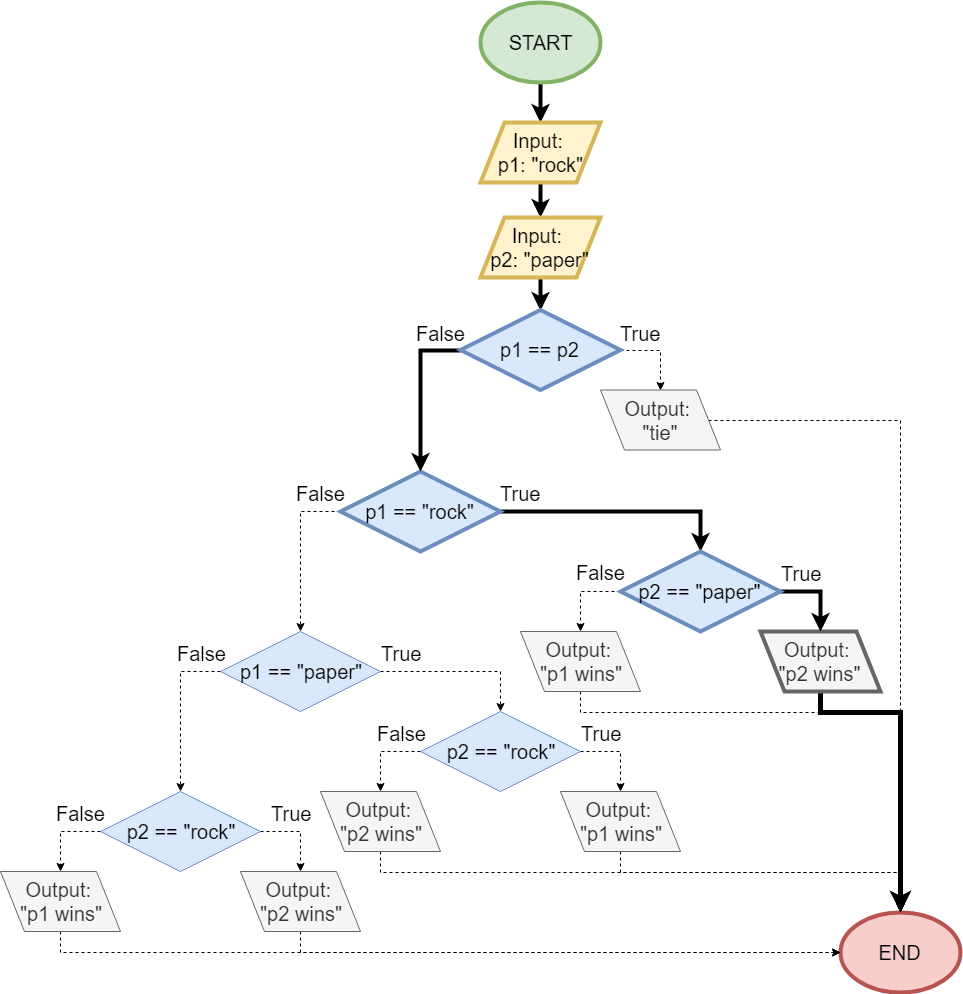
First, let’s look at the case when player 1 chooses “rock” and player 2 chooses “paper”. So, our variables would be p1 = "rock" and p2 = "paper". Here’s a trace of the path that input would follow through the flowchart:
As we can see, first the program will check to see if the inputs are equal. Since they are not, it will follow the false branch to the left. Then, it will determine if player 1’s input was "rock". Since that is the case, it will follow the true branch to the right. After that, the program will test if p2 == "paper", which is also true. So, the program will follow the right branch, and output p2 wins. We can see that this output is indeed correct, since the rules of the game states that “paper covers rock”, meaning that player 2’s choice of paper will beat player 1’s choice of rock.
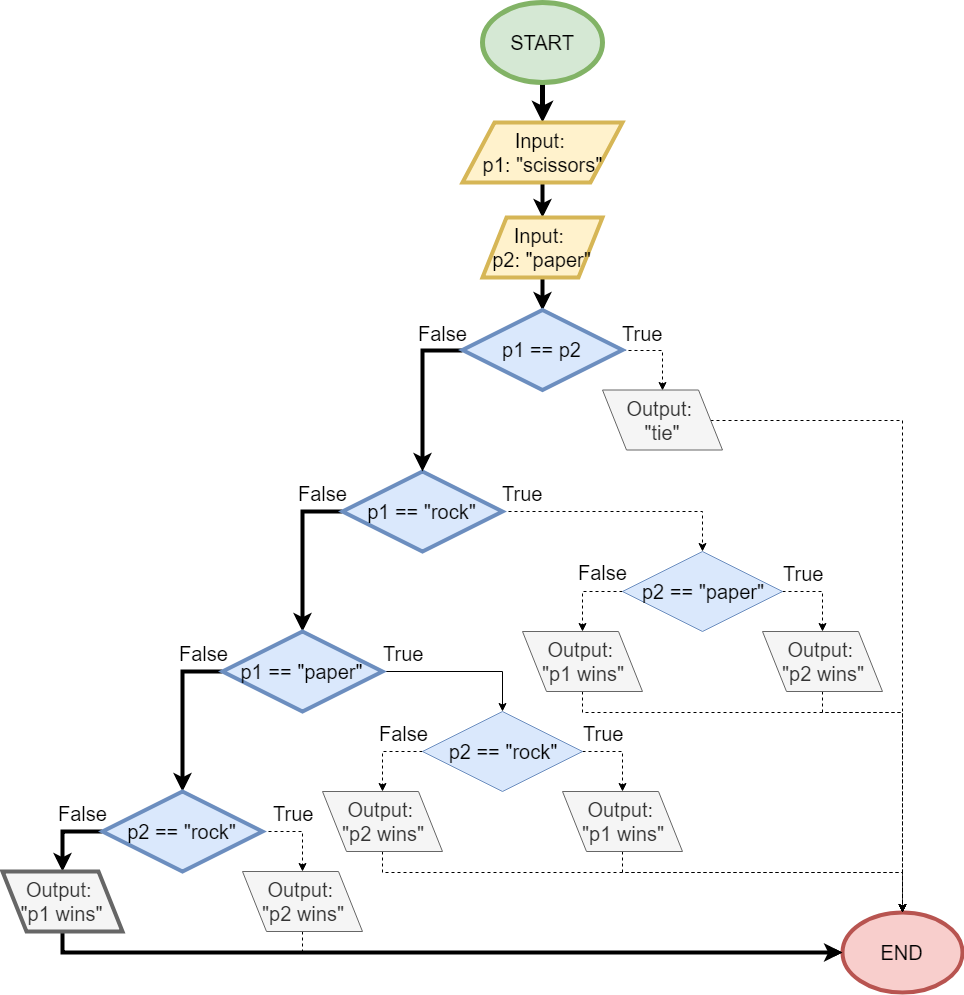
Let’s look at one other example. This time, player 1 chooses “scissors” and player 2 chooses “paper”. Here’s a flowchart representing our program with those inputs:
In this example, the program will first decide if the inputs are equal. They are not, so the program will once again follow the false branch to the left. Then, it will test to see if player 1’s input was "rock". In this case, the user input "scissors", so this test is false, and the program will choose the false branch to the left.
Next, it will try to determine if player 1’s input was "paper". Since that is also not the case, it will follow the false branch to the left once again.
At this point, our program knows that player 1 did not input either "rock" or "paper", so it can assume that the input must be "scissors". So, it will then check to see if player 2’s input was "rock". This is also false, so it will choose the false branch once again.
From earlier, it knows that player 2’s input is different from player 1, and player 2 did not input "rock". Since player 1’s input is assumed to be "scissors", that means that player 2 must have chosen "paper" as it is the only valid input left.
Therefore, this program has determined that player 1’s input was "scissors" and player 2’s input was "paper". By the rules of the game, “scissors cuts paper”, so player 1 wins. Our program will correctly output p1 wins!
In the examples above we made a very important assumption, which allowed us to infer information about each user’s input. Can you find a possible problem with the programs as shown in the diagrams above?
In those examples, we assumed that the users would only input either "rock", "paper", or "scissors". Based on that assumption, if we have determined that a player’s input was neither "rock" nor "paper", as we did in the last example, then we can infer that the user must have chosen "scissors".
However, we did not specify how that assumption was enforced in our diagram. In a real-world program, how to handle bad input is often specified, which can lead to additional decision boxes in the flowchart that would test each user’s input against a list of valid inputs before accepting it. This would make the flowchart significantly larger and more complex, which is why they were omitted for this example.
As you complete the programming examples and projects in this course, you’ll need to pay special attention to the program’s specifications and any assumptions made about possible user inputs. It will often be the case that there is no instructions given for handling bad input. In this case, our program should do nothing since it wasn’t specified. Adding unspecified features is a bad programming practice, so we want to avoid adding any instructions that are not explicitly listed in the program specification. In a formal development process, a “bug” would be opened to fix the specification first, and then we would update the code to match the new specification.
In most cases, it is always better to specify how a program handles invalid input instead of relying on assumptions about what your users may or may not provide as input.
The customer may always be right, but users should never be trusted to follow instructions!
As we can see, the ability to make decisions in a computer program is one of the most important building blocks we need to build more elaborate and complex programs. In this chapter, we’ll learn about all of the different ways we can write computer programs to make decisions and perform different actions based on those decisions using conditional constructs.