Example: Tower of Hanoi

There are some problems where an iterative solution is difficult to implement and is not always immediately intuitive, while a recursive solution is simple, concise and easy to understand. A classic example is the problem of the Tower of Hanoi.

The Tower of Hanoi is a game that lends itself to a recursive solution. Suppose we have three towers on which we can put discs. The three towers are indicated by a letter, A, B, or C.

Now, suppose we have $N$ discs all of different sizes. The discs are stacked on tower A based on their size, smaller discs on top. The problem is to move all the discs from one tower to another by observing the following rules:

1. we can move only one disc at a time, and we must move the disc that is at the top of a tower first, and
2. a larger disc can never be put on top of a smaller disc.

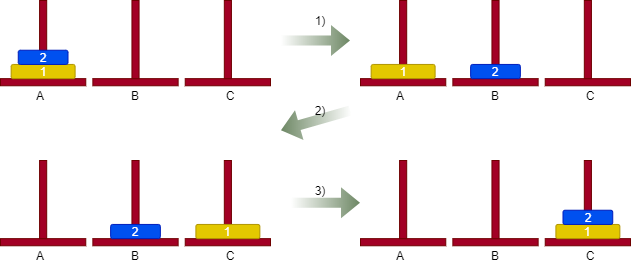
To try to solve the problem let’s start by considering a simple case: we want to move two discs from tower A to tower C. As a convenience, suppose we number the discs in ascending order by assigning the number 1 to the larger disc. The solution in this case is simple and consists of the following steps:

1. move disc 2 from tower A to tower B,
2. move disc 1 from tower A to tower C, and
3. move disc 2 from Tower B to tower C.

The following figure shows how the algorithm works.

It is a little more difficult with three discs, but after a few tries the proper algorithm emerges. With our knowledge of recursion, we can come up with a simple and concise solution. Since we already know how to move two discs from one place to another, we can solve the problem recursively.

1. Move discs 3 and 2 from tower A to B.
2. Move disc 1 from tower A to C.
3. Move discs 3 and 2 from tower B to C.

In formulating our solution, we assumed that we could move two discs from one tower to another, since we have already solved that part of the problem above. In step 1, we use this solution to move the top two discs from tower A to B. Then, in step 3, we again use that solution to move two discs from tower B to C. This process can now easily be generalized to the case of N discs as described below.

1. Move the first N-1 discs from tower A to B.
2. Move disc 1 from tower A to C.
3. Move N -1 discs from tower B to C.

The algorithm is captured in the following pseudocode. Here N is the total number of discs, ORIGIN is the tower where the discs are currently located, and DESTINATION is the tower where they need to be moved. Finally, TEMP is a temporary tower we can use to help with the move. All the parameters are integers.

function HANOI(N, ORIGIN, DESTINATION, TEMP)
    if N >= 0
        HANOI(N-1, ORIGIN, TEMP, DESTINATION)
        Move disc N from ORIGIN to DESTINATION
        HANOI(N-1, TEMP, DESTINATION, ORIGIN)
    end if
    return
end function

The function moves the $N$ discs from the source tower to the destination tower using a temporary tower. To do this, it calls itself to move the first $N-1$ discs from the source tower to the temporary tower. It then moves the bottom disc from the source tower to the destination tower. The function then moves the $N-1$ discs present in the temporary tower into the destination tower.

The list of movements to solve the three-disc problem is shown below.

1. move disc 3 from ORIGIN to DESTINATION
2. move disc 2 from ORIGIN to TEMP
3. move disc 3 from DESTINATION to TEMP
4. move disc 1 from ORIGIN to DESTINATION
5. move disc 3 from TEMP to ORIGIN
6. move disc 2 from TEMP to DESTINATION

Iterative solutions to the Tower of Hanoi problem do exist, but it took many researchers several years to find an efficient solution. The simplicity of finding the recursive solution presented here should convince you that recursion is an approach you should definitely keep in your bag of tricks!