Tree Operations
Along with understanding how trees work, we want to also be able to implement a tree of our own. We will now outline key components of a tree class.
MyTree
Recall that trees are defined recursively so we can build them from the leaves up where each leaf is a tree itself. Each tree will have three properties: the item it contains as an object, its parent node of type MyTree, and its children as a list of MyTrees. Upon instantiation of a new MyTree, we will set the item value and initialize the parent node to None and the children to an empty list of type MyTree.
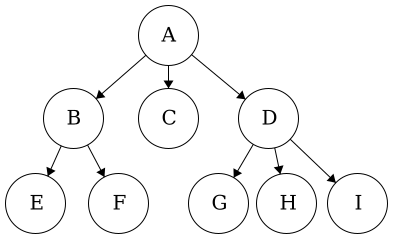
Suppose that we wanted to construct the following tree.
We would start by initializing each node as a tree with no parent, no children, and the item in this instance would be the characters. Then we build it up level by level by add the appropriate children to the respective parent.
Disclaimer: This implementation will not prevent all cycles. In the next module, we will introduce steps to prevent cycles and maintain true tree structures.
Finding a child
In this method, we will take a value as input and then check if that value is the item of a child of the current node. If the value is not the item for any of the node’s children then we should return none.
function FINDCHILD(VALUE)
FOR CHILD in CHILDREN
IF CHILD's ITEM is VALUE
return CHILD
return NONE
end functionGetting children, item, parent, or degree
Each of these will be rather straight forward; children, item, and parent are all attributes of our node, so we can have a getter function that returns the respective values. The slightly more involved task will be getting the degree. Recall that the degree of a node is equal to the number of children. Thus, we can simply count the number of children and return this number for the degree.
Checking node type
We will have two functions to check the node type: one to determine if the node is a leaf and one to determine if it is a root. The definition of a leaf is a node that has no children. Thus, to check if a node is a leaf, we can simply check if the number of children is equal to zero. Similarly, since the definition of a root is a node with no parent, we can check that the parent attribute of the node is None.
Adding a child
When we wish to add a child, we must fisrt make sure we are able to add the child.
- Check that the child is an instance of
MyTree - Make sure the child doesn’t already have a parent
- Make sure the child isn’t already a child of the parent
We will return true if the child was successfully added and false otherwise while raising the appropriate errors.
function ADDCHILD(CHILD)
IF CHILD has PARENT
throw exception
IF CHILD is CHILD of PARENT
return FALSE
ELSE
append CHILD to PARENT's children
set CHILD's parent to PARENT
return TRUE
end functionAs an example, lets walk through the process of building the tree above:
- Instantiate MyTree
awith item ‘A’ - Instantiate MyTree
bwith item ‘B’ - Instantiate MyTree
cwith item ‘C’ - Instantiate MyTree
dwith item ‘D’ - Instantiate MyTree
ewith item ‘E’ - Instantiate MyTree
fwith item ‘F’ - Instantiate MyTree
gwith item ‘G’ - Instantiate MyTree
hwith item ‘H’ - Instantiate MyTree
iwith item ‘I’ - Add child tree
gto treed - Add child tree
hto treed - Add child tree
ito treed - Add child tree
eto treeb - Add child tree
fto treeb
Once we have completed that, visually, we would have the tree above and in code we would have:
- MyTree
awith parent_node = None, item = ‘A’, children = {b,c,d} - MyTree
bwith parent_node =a, item = ‘B’, children = {e,f} - MyTree
cwith parent_node =a, item = ‘C’, children = { } - MyTree
dwith parent_node =a, item = ‘D’, children = {g,h,i} - MyTree
ewith parent_node =b, item = ‘E’, children = { } - MyTree
fwith parent_node =b, item = ‘F’, children = { } - MyTree
gwith parent_node =d, item = ‘G’, children = { } - MyTree
hwith parent_node =d, item = ‘H’, children = { } - MyTree
iwith parent_node =d, item = ‘I’, children = { }
Note: When adding a child we must currently be at the node we want to be the parent. Much like when you want to add a file to a folder, you must specify exactly where you want it. If you don’t, this could result in a wayward child.
Removing a child
In the case of removing a child, we first need to check that the child we are attempting to remove is an instance of MyTree. We will return true if we successfully remove the child and false otherwise.
function REMOVECHILD(CHILD)
IF CHILD in PARENT'S children
REMOVE CHILD from PARENT's children
SET CHILD's PARENT to NONE
return TRUE
ELSE
return FALSE
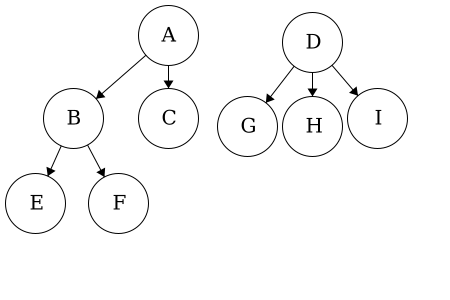
end functionAs with adding a child, we need to ensure that we are in the ‘right place’ when attempting to remove a child. When removing a child, we are not ’erasing’ it, we are just cutting the tie from parent to child and child to parent. Consider removing d from a. Visually, we would have two disjoint trees, shown below:
In code, we would have:
- MyTree
awith parent_node = None, item = ‘A’, children = {b,c} - MyTree
bwith parent_node =a, item = ‘B’, children = {e,f} - MyTree
cwith parent_node =a, item = ‘C’, children = { } - MyTree
dwith parent_node = None, item = ‘D’, children = {g,h,i} - MyTree
ewith parent_node =b, item = ‘E’, children = { } - MyTree
fwith parent_node =b, item = ‘F’, children = { } - MyTree
gwith parent_node =d, item = ‘G’, children = { } - MyTree
hwith parent_node =d, item = ‘H’, children = { } - MyTree
iwith parent_node =d, item = ‘I’, children = { }