Recursive Linear Search
We looked at an iterative version of the find function above. But what would it take to turn that function into a recursive function? While for this particular function, there is not a lot to be gained from the recursive version, it is still instructive to see how we would do it. We will find recursive functions more useful later on in the module.
In this case, to implement a recursive version of the function, we need to add a third parameter, index, to tell us where to check in the array. We assume that at the beginning of a search, index begins at 0. Then, if number is not in location index in the array, index will be incremented before making another recursive call. Of course, if number is in location index, we will return the number of index. The pseudocode for the findR function is shown below.
1function FINDR (NUMBER, ARRAY, INDEX)
2 if INDEX >= size of ARRAY then
3 return -1
4 else if ARRAY[INDEX] == NUMBER
5 return INDEX
6 else
7 return FINDR (NUMBER, ARRAY, INDEX + 1)
8 end if
9end functionFirst, we check to see if index has moved beyond the bounds of the array, which would indicate that we have searched all the locations in array for number. If that is the case, then we return -1 in line 3 indicating that we did not find number in array. Next, we check to see if number is found in array[index] in line 4. If it is, the we are successful and return the index. However, if we are not finished searching and we have not found number, then we recursively call findR and increment index by 1 to search the next location.
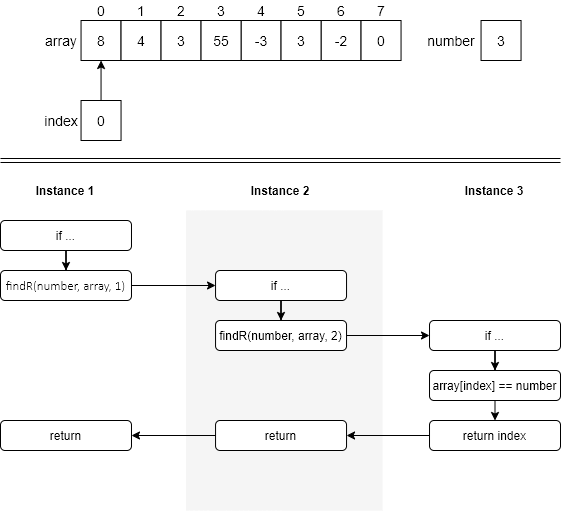
An example of using the findR function is shown below. The top half of the figure shows the state of the data in the initial call to the findR function (instance 1). The bottom half of the figure shows the recursive path through the function. The beginning of instance 1 shows the if statement in line 2. In instance 1, since we have not searched the entire array (line 2) and array[0] is not equal to number (line 4), we fall down to the else part function and execute line 7, the recursive call. Since index is 0 in instance 1, we call instance 2 of the function with an index of 1.
In instance 2, the same thing happens as in instance 1 and we fall down to the else part of the if statement. Once again, we call a new instance of findR, this time with index set at 2. Now, in instance 3, array[index] is equal to number in line 4 and so we execute the return index statement in line 5. The value of index (2) is returned to instance 2, which, in line 7, simply returns the value of 2 to instance 1. Again, in line 7, instance 1 returns that same value (2) to the original calling function.
Notice that the actual process of searching the array is the same for both the iterative and recursive functions. It is only the implementation of that process that is different between the two.