Binary Search
Now that we’ve learned how to sort the data in our container, let’s go back and revisit the concept of searching once again. Does our approach change when we know the data has been sorted?
Our intuition tells us that it should. Recall that we discussed how much easier it would be to find a particular paper in a sorted filing cabinet rather than just searching through a random pile of papers on the floor. The same concept applies to data in our programs.
The most commonly used searching algorithm when dealing with sorted data is binary search. The idea of the algorithm is to compare the value in the middle of the container with the value we are looking for. In this case, let’s assume the container is sorted in ascending order, so the smaller elements are before the larger ones. If we compare our desired value with the middle value, there are three possible outcomes:
- the value in the middle is equal to the desired value. We have found the element!
- the value in the middle is less than the desired value. Since the container is ordered in ascending order, we must search for the value in the second half of the container.
- the value in the middle is greater than the desired value. Since the container is ordered in ascending order, we must search for the value in the first half of the container.
Once an occurrence of the desired value is found, we can also look at the values before it to see if there any more of the desired values in the container. Since it is sorted, they should all be grouped together. If we want our algorithm to return the index of the first occurrence of the desired value, we can simply move toward the front of the array until we find that first occurrence.
Binary Search Example
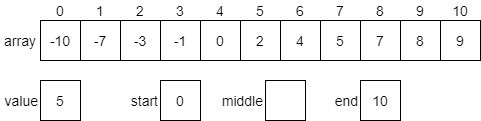
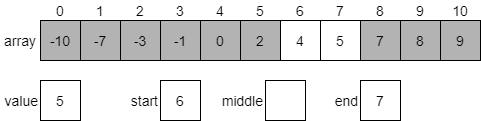
Let’s work through a quick example of the binary search algorithm to see how it works in practice. Let’s assume we have the array shown in the diagram below, which is already sorted in ascending order. We wish to find out if the array contains the value 5. So, we’ll store that in our value variable. We also have variables start and end representing the first and last index in the array that we are considering.
First, we must calculate the middle index of the array. To do that, we can use the following formula.
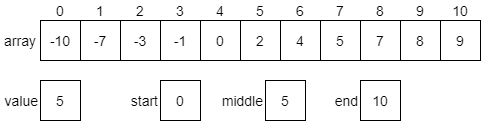
$$ \text{int}((\text{start} + \text{end}) / 2) $$In this case, we’ll find that the middle index is 5.
Next, we’ll compare our desired value with the element at the middle index, which is 2. Since our desired value 5 is greater than 2, we know that 5 must be present in the second half of the array. We will then update our starting value to be one greater than the middle element and start over. In practice, this could be done either iteratively or recursively. We’ll see both implementations later in this section. The portion of the array we are ignoring has been given a grey background in the diagram below.
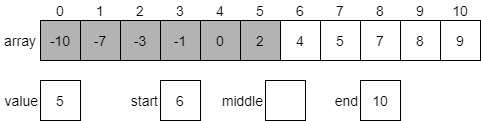
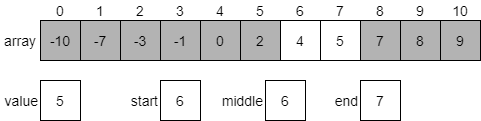
Once again, we’ll start by calculating a new middle index. In this case, it will be 8.
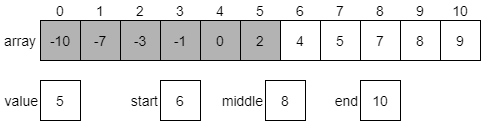
The value at index 8 is 7, which is greater than our desired value 5. So we know that 5 should be in the first half of the array from index 6 through 10. We need to update the end variable to be one less than middle and try once again.
We’ll first calculate the middle index, which will be 6. This is because (6 + 7) / 2 is 6.5, but when we convert it to an integer it will be truncated, resulting in just 6.
Since the value at index 6 is 4, which is less than our desired value 5, we know that we should be looking at the portion of the array which comes after our middle element. Once again, we’ll update our start index to be one greater than the middle and start over.
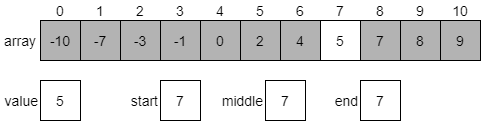
In this case, since both start and end are the same, we know that the middle index will also be 7. We can compare the value at index 7 to our desired value. As it turns out, they are a match, so we’ve found our value! We can just return middle as the index for this value. Of course, if we want to make sure it is the first instance of our desired value, we can quickly check the elements before it until we find one that isn’t our desired value. We won’t worry about that for now, but it is something that can easily be added to our code later.