Max and Min - Pairs

Another solution consists of comparing the numbers in pairs, instead of one at a time.

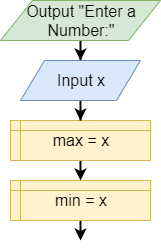
Base Case

When we have received just one number, this number is both the maximum and the minimum. In the initial state, you have max holding the maximum, and min holding the minimum. The invariant is the following:

1. The variable max holds the maximum of all the numbers considered so far
2. The variable min holds the minimum of all the numbers considered so far

The algorithm is depicted by the following flowchart and pseudocode:

print "Enter a Number:"
input X
MAX = X
MIN = X

The Next Two Numbers

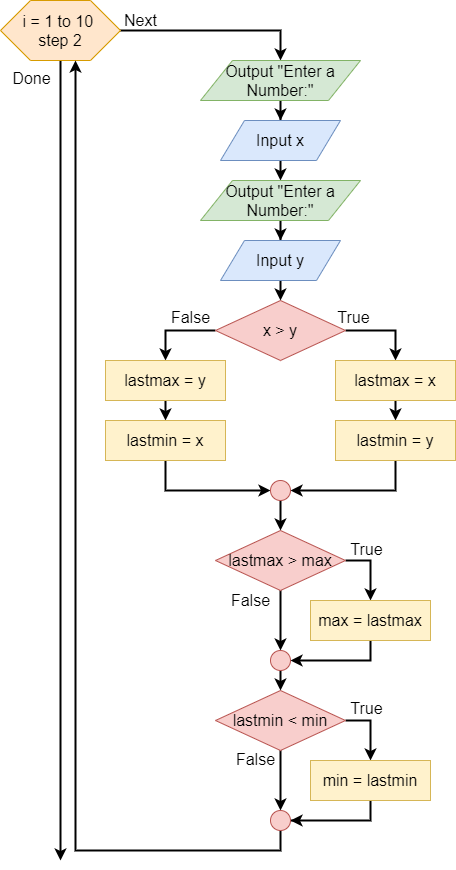
In this program, instead of just considering one number at a time, we’ll ask the user to input two numbers. Then, we can determine which of those two inputs is larger (we’ll call it lastmax), and compare it to the value in max. Similarly, we can do the same for the smaller value (called lastmin) and min. Would this program be more efficient?

The algorithm is depicted by the following flowchart and pseudocode:

loop I from 1 to 10 step by 2:
    output "Enter a Number:"
    input X
    output "Enter a Number:"
    input Y
    if X > Y
        LASTMAX = X
        LASTMIN = Y
    else
        LASTMAX = Y
        LASTMIN = X
    end if
    if LASTMAX > MAX
        MAX = LASTMAX
    end if
    if LASTMIN < MIN
        MIN = LASTMIN
    end if
end loop

Once again, we can easily show that the same loop preconditions, postconditions, and invariants work for this loop:

• Loop preconditions:
  1. The variable max holds the maximum value among all the numbers considered so far
  2. The variable min holds the minimum value among all the numbers considered so far
  3. The new inputs considered are a number
• Loop postconditions:
  1. The variable max holds the maximum value among all the numbers considered so far
  2. The variable min holds the minimum value among all the numbers considered so far
• Loop invariant:
  1. The variable max holds the maximum value among all the numbers considered so far
  2. The variable min holds the minimum value among all the numbers considered so far

A full flowchart of this program can be found by clicking the following link:

Min Max Flowchart

It is helpful to have this diagram available in a second browser tab for review on the next few pages.