Doubly Linked Lists - Insertion

Insertion in doubly linked lists is similar to what we saw in the singly linked list with two exceptions:

1. We must update both the previous and next pointers in all affected nodes.
2. We can use the tail pointer to make the insertion of data at the end of the list very efficient.

Inserting at the Beginning

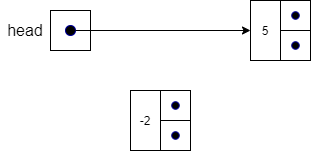
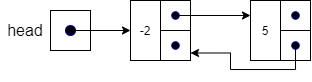
Inserting at the beginning of a doubly linked list is almost as straightforward as in a singly linked list. We just need to make sure that we update the previous pointer in each affected node. After creating the new node in line 1, we check to see if the list is empty in line 2. If it is empty, then we only have to worry about updating the head and tail pointers to both point at node in lines 3 and 4. If the list is not empty, we have the situation shown below.

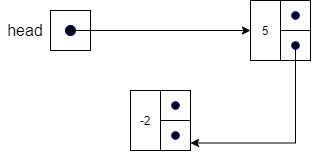
To insert a node at the beginning of the list, we set head.previous (the previous pointer in the first node in the list) to point to the new node in line 5.

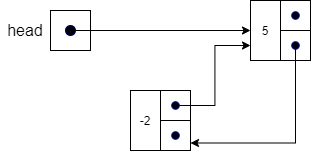
Next, we set the next pointer in the new node to point to where head is currently pointing in line 6, which is the first node in the list.

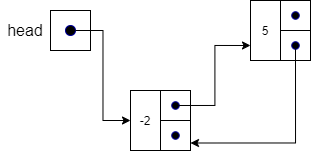
Finally, we update head to point to the new node and then increment the size in line 8.

With a little bit of reformatting, we can see that we’ve successfully inserted our new node in the list.

The pseudocode for this operation is given below.

function prepend(data)
	node = new Node(data)	    (1)
	if size == 0	            (2)
		head = node	            (3)
		tail = node	            (4)
	else
		head.previous = node	(5)
		node.next = head	    (6)
		head = node	            (7)
	end 
	size = size + 1	            (8)
end function

Since there are no loops in the prepend code, the code runs in constant time.

Inserting in the Middle

Inserting a new node at some arbitrary index in a doubly linked list is similar to the same operation in a singly linked list with a couple of changes.

1. If the index is at the end of the list, we can use an efficient append operation (defined below) to insert the node at the end of the list.
2. When walking through the list to the correct index, we do not need to keep track of the previous node.
3. We will have to update both the previous and next pointers in all affected nodes.

Lines 1 and 2 in the code check to ensure that the index is a valid number, then we check to see if we are inserting at the beginning or end of the list in lines 2 and 4. If we are, we simply call the appropriate method, either prepend or append.

If none of those conditions exist, then we start the process of walking through the list to find the node at index. To do this, we need to create the new node we want to insert and then create a temporary pointer curr that we will use to point to the current node on our walk.

Lines 10 and 11 form the loop that walks through the list until we get to the desired index. When the loop ends, we will want to insert the new node between curr and curr.next. Thus, we set the appropriate values for the new node’s next and previous pointers in line 12 and 13. Then, we set the previous pointer in node.next to point back to node in line 14 and then set curr.next to point at the new node. Finally, we increment size by 1.

function insertAt(data, index)
	if index < 0 OR index > size	(1)
		raise exception	            (2)
	else if index == 0	            (3)
		prepend(data)	            (4)
	else if index == size	        (5)
		append(data)	            (6)
	else				            (7)
		node = new node(data)	    (8)
		curr = head	                (9)

		for i = 1 to index -1	    (10)
			curr = curr.next	    (11)
		end for

		node.next = curr.next	    (12) 
		node.previous = curr	    (13)
		node.next.previous = node	(14)
		curr.next = node	        (15)
		size = size + 1	            (16)
	end if
end function

Although prepend and append run in constant time, the general case will cause us to walk through the list using a for loop. Therefore, the insertAt operation runs in order $N$ time.

Inserting at the End

Since we have added the tail pointer to the doubly linked list class, we can make adding a node at the end of the list run in constant time instead of order $N$ time. In fact, if you look at the code below for the append operation, it is exactly the same as the constant time prepend operation except we have replaced the head pointer with the tail pointer in lines 5 – 7.

function append(data)
	node = new node(data)	     (1)
	if size == 0	             (2)
		tail = node	             (3)
		head = node	             (4)
	else
		tail.next = node	     (5)
		node.previous = tail 	 (6)
		tail = node	             (7)
	end if
	size = size + 1	             (8)
end function