Basic Operations

We have already seen the pseudocode for the two key operations for queues: enqueue and dequeue. However, there are several others that make the queue data structure much easier to use:

• enqueue—places an item on the end of the queue,
• dequeue—removes and returns the item at the start of the queue,
• peek—returns the item at the start of the queue without removing it,
• isEmpty—returns true if there are no items in the queue,
• isFull—returns true if our queue array is full, and
• size—returns the number of items in the queue.

We will discuss each of these operations. But first, let’s talk about the constructor for the queue class and what it must do to properly set up a queue object.

Constructor

The main responsibility of the constructor is to initialize all the attributes in the queue class. As we discussed above, the attributes include the myQueue array and the start and end variables that hold indexes into myQueue.

Since we are using an array for our queue, we will need to know how big to make the array in our constructor. There are two options. We could just use a default size for the array. Or, we could allow the user to pass in a positive integer to set the size. In this module we assume the caller must provide a capacity value, which must be greater than 0.

function QUEUE (CAPACITY)
	if CAPACITY is not an integer then		(1)
		throw exception				        (2)
	else if CAPACITY <= 0 then			    (3)
		throw exception				        (4)
	end if
	MYQUEUE = new array of size capacity	(5)
    START = -1						        (6)
    END = 0						            (7)
end function

The first thing we do in the code is to check to make sure that capacity is actually an integer that is greater than 0. Essentially, this is our precondition for the method. If our precondition is not met, we throw an exception. (If we are using a typed language such as Java, we can enforce our precondition by requiring that capacity be of type integer instead of explicitly checking it in the code.) Once we’ve validated our precondition, we create a new array of size capacity for the myQueue array and set the attribute start to -1 and end to 0.

Enqueue

We have already discussed the enqueue operation and seen it in operation above. In the pseudocode below, we see that we must first check to ensure that the queue is not already full. Again, this is our precondition.

function ENQUEUE (item)
	if ISFULL() then			          (1)
		raise exception			          (2)
	end if	
	MYQUEUE[END] = ITEM			          (3)
	END = (END + 1) % length of MYQUEUE	  (4)
	if START == -1				          (5)
		START = 0				          (6)
	end if
end function

Once our precondition is validated, we simply increment and store the item into the array at index end. Then we increment end, using the modulo operator to wrap end to point to the beginning of the array if warranted. Next, we check for the condition of an empty queue. If start = 1, then we know the queue is empty, so we set start = 0. The enqueue function does not return a value.

Because there are no loops in the enqueue function, the function operates in constant time regardless of the size of the array or the number of items in it.

Dequeue

Like enqueue, we have already seen the dequeue operation. It simply takes the first item from the start of the queue and returns it. However, before we can do that, we need to validate our precondition. For the dequeue operation, our precondition is that the queue must not already be empty, which is detected by the isEmpty function in line 1.

function DEQUEUE ()
    if ISEMPTY() then					        (1)
		raise exception					        (2)
    end if 
	ITEM = MYQUEUE[START]					    (3)
	START = (START + 1) % length of MYQUEUE		(4)
	if START == END						        (5)
		START = -1						        (6)
		END = 0						            (7)
	end if
	return ITEM							        (8)
end function

Once we have validated our precondition, we simply copy the item from the myQueue[start] in line 3 and increment start. Again, we use the modulo operator in line 4 to wrap start back to 0 if it is needed. Next, we check to see if the myQueue is empty, and, if it is, reset the values of start and end back to their initial values. Finally, we return the item to the calling function in line 8. Like the enqueue operation, the dequeue function operates in constant time.

Peek

The peek operation returns the item at the start of the queue, without removing it from the array. Like the dequeue operation it has the precondition that the queue must not be empty. The pseudocode for the peek operation is shown below. It is also a constant time operation.

function PEEK()					(1)
    if ISEMPTY() then			(2)
		raise exception			(3)
    else	
		return MYQUEUE[START]	(4)
    end if 
end function

isFull

To allow the calling program to detect when the queue is full, we define an isFull operation. Notice that code external to the queue class cannot access the value of start or end so it cannot simply check if start == end on its own. In this case, the operation is very simple as we only need to return the Boolean value of start == end as shown below. There is no precondition for isFull and isFull operates in constant time.

function ISFULL()
	return START == END				(1)
end function

isEmpty

The isEmpty operation is very similar to the isFull operation except that we return the Boolean value of the condition start == -1 instead of start == end.

function ISEMPTY()
	return START == -1				(1)
end function

Size

This size method returns the number of items in the queue. However, it is not as straightforward as it might sound. Actually, there are several cases that we must consider, based on the fact that both start and end can “wrap around” the end of the array:

1. start == -1—the queue is empty, and size = 0,
2. start == end—the queue is full, and size equals the capacity of the array,
3. start < end—size = end – start, and
4. start > end—size = capacity of array - start + end + 1.

Thus, in our function, we simply need to check four conditions.

function SIZE()
	if START = -1							            (1)
		return 0							            (2)
	else if START == END					            (3)
		return capacity of MYQUEUE			            (4)
	else if START < END						            (5)
		return END – START					            (6)
	else	
		return capacity of MYQUEUE – START + END		(7)
	end if
end function

Notice that the conditions that are checked in lines 3 and 5 ensure that start must be greater than end. Therefore, we can simply use an else statement to capture the last case in line 7. Once again, this is a constant time function.

doubleCapacity

The doubleCapacity operation doubles the size of the array holding our queue. If we started with an array of size 4, the doubleCapacity operation will result in an array of size 8 with the contents of our original array stored in it. Unfortunately, most programming languages (like Java) do not simply let you double the size of the array. A noted exception to this is Python, which does allow you to directly extend an array.

In a traditional programming language, the easiest way to accomplish the doubleCapacity operation is to complete the following steps:

1. Create a new array with twice the capacity of the existing array,
2. Copy the contents of original array into the new array,
3. Update the start and end variables to point at the correct elements, then
4. Point the myQueue array at the new array.

The pseudocode for the doubleCapacity operation is shown below.

function DOUBLECAPACITY()
    NEWQUEUE = new array of MYQUEUE capacity * 2	(1)
    LENGTH = SIZE()						            (2)
    for I = 0 to LENGTH - 1					        (3)
        NEWQUEUE[I] = DEQUEUE()				        (4)
    end for
    START = 0							            (5)
    END = LENGTH						            (6)
    MYQUEUE = NEWQUEUE					            (7)
end function

In the function, we create the new array in line 1 and then save the total number of items in the array for use later in line 2. Next, we use a for loop in lines 3 and 4 to copy the contents from myQueue into newQueue. Since the contents of myQueue are not necessarily stored neatly in the array (i.e., from $0$ to $n$), it is easier for us to use the existing size and dequeue functions to get access to each item in the queue in order. Once we have copied the items from myQueue to newQueue, we simply need to set the start and end variables in line 5 and 6, and then set myQueue = newQueue in line 7 to complete the process.

The doubleCapacity operation is not a constant time operation since copying the contents of the original array into the new array requires us to copy each item via a loop. This requires $N$ steps. Thus, we would say that doubleCapacity runs in “order $N$” time.

halveCapacity

The halveCapacity operation is similar to the doubleCapacity operation except that we now have a precondition. We must make sure that when we reduce the space for storing the queue that we still have enough space to store all the items currently in the queue. For example, if we have 10 items in a queue with a capacity of 16, we can’t successfully perform halveCapacity. Doing so would only leave us a queue with a capacity of 8 and we would not be able to fit all 10 items in the new queue.

The pseudocode for the halveCapacity function is shown below, with the precondition being checked in line 2. Once we create newQueue to be half the capacity of myQueue in line 4, the remainder of the function is exactly the same as the doubleCapacity function, since lines 5-10 are just concerned with copying the items from myQueue to newQueue and setting the associated variables.

function HALVECAPACITY()
	if SIZE() > MYQUEUE capacity / 2 then		    (2)
		throw exception					            (3)
	end if
    NEWQUEUE = new array of MYQUEUE capacity / 2	(4)
    LENGTH = SIZE()						            (5)
    for I = 0 to LENGTH - 1					        (6)
        NEWQUEUE[I] = DEQUEUE()				        (7)
    end for
    START = 0							            (8)
    END = LENGTH % length of NEWQUEUE	            (9)
    MYQUEUE = NEWQUEUE					            (10)
end function

Like the doubleCapacity operation, halveCapacity is not a constant time operation since copying the contents of the original array requires us to loop $N$ times. So, halveCapacity runs in “order $N$” time.

toString

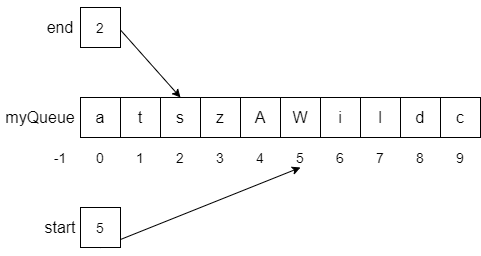
The toString function returns a string that concatenates the strings representing all the items stored in an array. In most programming languages, each object class must implement the toString operation. For instance, in the queue below where each item is a character, if we called myQueue.toString(), we would expect to be returned the string "Wildcats".

Notice that we must read the queue array from start to end to get the proper output string.

In the pseudocode below we first create an empty string called output in line 1. Then, we create a loop in line 2 that counts using i the number of items in the queue from 0 to the size of the queue. However, we can’t use this counter i to directly index into the array, since start and end may be almost anywhere in the array. Thus, we use i to compute next in line 3, which we will use as our index into the array. Our index i should begin with start and finish with the end value, which can also be computed as start + size() – 1 modulo the capacity of myQueue. We then use the index next in line 4 to select the appropriate element of myQueue to append to our output string. Once the loop ends, we simply return our output string.

function TOSTRING()
    OUTPUT = ""								          (1)
    for I = 0 to SIZE() - 1						      (2)
        NEXT = (START + I) % MYQUEUE capacity		  (3)
        OUTPUT = OUTPUT + MYQUEUE[next].TOSTRING()	  (4)
    end for								              (5)
    return OUTPUT							          (6)
end function

The toString function includes a loop that, at most, looks at each element in myQueue; therefore, toString executes in order $N$ time.