Greedy

Another algorithmic technique that we’ll learn about is the greedy technique. In a greedy algorithm, the program tries to build a solution one piece at a time. At each step, it will act “greedy” by choosing the piece that it thinks is the best choice for the solution based on the available information. Instead of trying every possible solution like a brute force algorithm or dividing the problem into smaller parts like the divide and conquer approach, a greedy algorithm will just try to construct the one best answer it can.

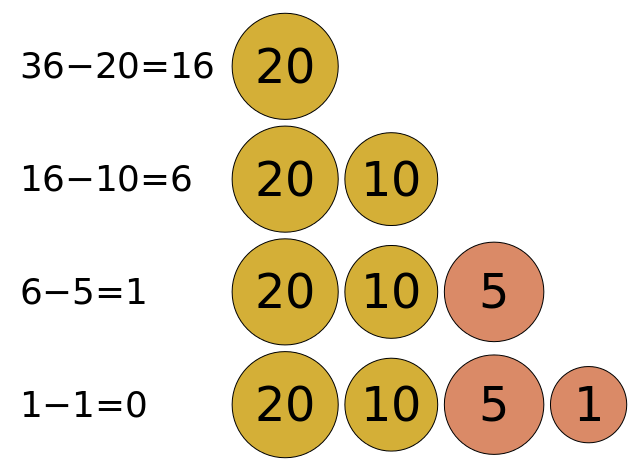
^[File:Greedy algorithm 36 cents.svg. (2019, April 27). Wikimedia Commons, the free media repository. Retrieved 23:19, February 8, 2020 from https://commons.wikimedia.org/w/index.php?title=File:Greedy_algorithm_36_cents.svg&oldid=347456702.]

Example

For example, we can use a greedy algorithm to determine the fewest number of coins needed to give change, as shown in the example above. If the customer is owed $36$ cents, and we have coins worth $20$ cents, $10$ cents, $5$ cents and $1$ cent, how many coins are needed to reach $36$ cents?

In a greedy solution, we could choose the coin with the highest value that is less than the change required, give that to the customer, and subtract its value from the remaining change. In this case, it will indeed produce the optimal solution.

In fact, both the United States dollar and the European euro have a system of coins that will always produce the minimum number of coins with a greedy algorithm. So that’s very helpful!

However, does it always work? What if we have a system that has coins worth $30$ cents, $18$ cents $4$ cents, and $1$ cent. Would a greedy algorithm produce the result with the minimum number of coins when making change for $36$ cents?

Let’s try it and see. First, we see that we can use a $30$ cent coin, leaving us with $6$ cents left. Then, we can use a single $4$ cent coin, as well as two $1$ cent coins for a total of $4$ coins: $30 + 4 + 1 + 1 = 36$.

Is that the minimum number of coins?

It turns out that this system includes a coin worth $18$ cents. So, to make $36$ cents, we really only need $2$ coins: $18 + 18 = 36$!

This is the biggest weakness of the greedy approach to algorithm design. A greedy algorithm will find a possible solution, but it is not guaranteed to be the best possible solution. Sometimes it will work just fine, but other times it may produce solutions that are not very good at all. So we always must consider that when creating an algorithm using a greedy technique.