2D and 1D Arrays
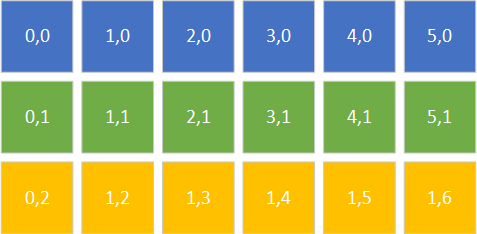
Let’s talk briefly about how a 2d array is actually stored in memory. We like to think of it as looking something like this visualization:
But in reality, it is stored linearly, like this:
To access a particular element in the array, the 2d coordinates must be transformed into a 1d index. Note that each row follows the proceeding rows, so the starting index of each row would be the width of the row, plus the x-coordinate, i.e. the index of $ (3,1) $ would be $ 1 * width + 3 $:
This can be generalized into the equation:
$$ i = y * width + x $$And the reverse operation, converting an index into 2d coordinates, would be:
$$ x = i \\\% width $$ $$ y = i / width $$
Note that we are using integer division and modulus in these equations, as the $ y $ value is the number of full rows (i.e. $ width $), and the $ y $ is the distance into the partial row (i.e. the remainder).
Thus, all we need to treat a 1d array as a 2d array (in addition to the data) is the width of the array. The height is only needed to calculate the array size (and thus the upper bound), which would be:
$$ size = width * height $$The C# Multidimensional Array simply builds on this concept, wrapping the array data in an object (note that for each dimension, you will have a corresponding size for that dimension, i.e. width, height, and depth for a 3d array).
Efficiency and 2d Arrays
Now, a note on efficiency - iterating through a C# multi-dimensional array is slower than the corresponding 1d array, as the interpreter optimizes 1d array operations (see What is Faster In C#: An int[] or an int[,] for a technical discussion of why). With that in mind, for a game we’ll always want to use a 1d array to represent 2d data.
A second note on efficiency. The order in which you iterate over the array also has an impact on efficiency. Consider an arbitrary 2d array arr implemented as a 1d array with width and height.
What would be the difference between loop 1:
int sum = 0;
for(int x = 0; x < width; x++)
{
for(int y = 0; y < height; y++)
{
sum += arr[y * width + x]
}
}And loop 2:
int sum = 0;
for(int y = 0; y < height; y++)
{
for(int x = 0; x < width; x++)
{
sum += arr[y * width + x]
}
}You probably would think they are effectively the same, and logically they are - they both will compute the sum of all the elements in the array. But loop 2 will potentially run much faster. The reason comes down to a hardware detail - how RAM and the L2 and L1 caches interact.
When you load a variable into a hardware register to do a calculation, it is loaded from RAM. But as it is loaded, the memory containing it, and some of the memory around it is also loaded into the L2 and L1 caches. If the next value in memory you try to access is cached, then it can be loaded from the cache instead of RAM. This makes the operation much faster, as the L2 and L1 caches are located quite close to the CPU, and RAM is a good distance away (possibly many inches!).
Consider the order in which loop 1 accesses the array. It first accesses the first element in the first row. Then the first element in the second row, and then the first element in the third row, then the second element in the first row, and so on… You can see this in the figure below:
Now, consider the same process for Loop 2:
Notice how all the memory access happens linearly? This makes the most efficient use of the cached data, and will perform much better when your array is large.