Trigonometry

Trigonometry - the math that deals with the side lengths and angles of triangles, plays an important role in many games. The trigonometric functions Sine, Cosine, and Tangent relate to the ratios of sides in a right triangle:

$$ \sin{A} = \frac{opposite}{hypotenuse} = \frac{a}{c} \tag{0} $$ $$ \cos{A} = \frac{adjacent}{hypotenuse} = \frac{b}{c} \tag{1} $$ $$ \tan{A} = \frac{opposite}{adjacent} = \frac{a}{b} \tag{2} $$

You can use the System.MathF library to compute $ \sin $, $ \cos $ using float values:

MathF.Sin(float radians) computes the $ \sin $ of the supplied angle
MathF.Cos(float radians) computes the $ \cos $ of the supplied angle
MathF.Tan(float radians) computes the $ \tan $ of the supplied angle

You can inverse these operations (compute the angle whose $ \sin $, $ \cos $, or $ \tan $ matches what you supply) with:

MathF.Asin(float s) computes the angle which produces the supplied $ \sin $ value
MathF.Acos(float c) computes the angle which produces the supplied $ \cos $ value
MathF.Atan(float t) computes the angle which produces the supplied $ \tan $ value
MathF.Atan2(float x, float y) computes the angle with produces the supplied x/y ratio. This form can be helpful to avoid a division by 0 error if y is 0.

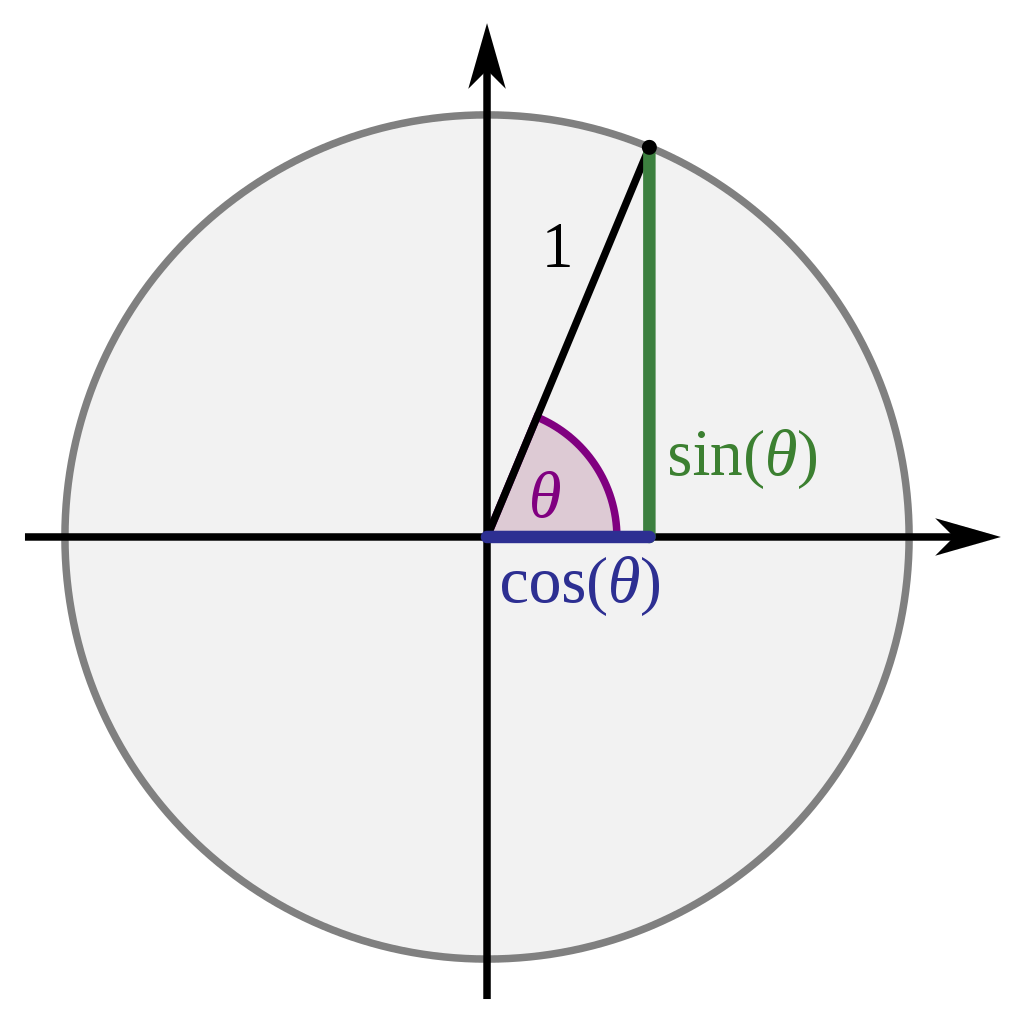
These angles are measured in radians - fractions of $ \pi $. Positive angles rotate counter-clockwise and negative ones clockwise. It can be helpful to consider radians in relation to the unit circle - a circle with radius 1 centered on the origin:

The angle of $ 0 $ radians falls along the x-axis. MonoGame provides some helpful float constants for common measurements in radians:

MathHelper.TwoPi represents $ 2\pi $, a full rotation around the unit circle ( $ 360^{\circ} $).
MathHelper.Pi represents $ \pi $, a half-rotation around the unit circle ( $ 180^{\circ} $).
MathHelper.PiOver2 represents $ \frac{\pi}{2} $, a quarter rotation around the unit circle ( $ 90^{\circ} $).
MathHelper.PiOver4 represents $ \frac{\pi}{4} $, an eighth rotation around the unit circle ( $ 45^{\circ} $).

Inside the unit circle you can inscribe a right triangle with angle at the origin of $ \theta $. This triangle has a hypotenuse with length 1, so $ \sin{\theta} $ is the length of the opposite leg of the triangle, and $ \cos{\theta} $ is the length of the adjacent leg of the triangle. Of course $ \tan{\theta} $ will always equal $ 1 $.